
- •Введение
- •Основные понятия теории вероятностей
- •1.1. События и действия над ними
- •1.2. Определение вероятности
- •1.3. Элементы комбинаторики
- •1.4. Условная вероятность события
- •1.5. Вероятность суммы двух событий
- •1.6. Формула полной вероятности. Формула Байеса
- •Упражнения
- •2. Повторные независимые испытания
- •2.1. Формула Бернулли
- •2.2. Формула Пуассона
- •2.3. Локальная и интегральная формулы Муавра-Лапласа
- •2.4. Полиномиальная схема
- •Упражнения
- •3. Случайные величины
- •3.1. Закон распределения случайной величины
- •Математические операции над случайными величинами
- •3.3. Математическое ожидание и дисперсия дискретной случайной величины
- •3.4. Функция распределения случайной величины
- •3.5. Непрерывные случайные величины
- •Упражнения
- •4. Основные законы распределения
- •4.1. Биномиальное распределение
- •4.2. Закон распределения Пуассона
- •4.3. Равномерный закон распределения
- •4.4. Показательный закон распределения
- •4.5. Нормальный закон распределения
- •Упражнения
- •5. Закон больших чисел и предельные теоремы
- •5.1. Неравенство Маркова
- •5.2. Неравенство Чебышева
- •5.3. Теорема Чебышева
- •5.4. Центральная предельная теорема
- •Упражнения
- •6. Однородные цепи Маркова
- •Упражнения
- •7. Занимательная теория вероятностей
- •7.1. Занимательные задачи
- •7.2. Парадоксы теории вероятностей
- •Упражнения
- •9. Статистическое распределение выборки
- •Упражнения
- •Упражнения
- •11. Статистические оценки параметров распределения
- •11.1. Точечные оценки
- •Упражнения
- •11.2. Интервальные оценки
- •Упражнения
- •Упражнения
- •13. Статистическая проверка гипотез о вероятностях,
- •средних, дисперсиях. Критерий согласия Пирсона
- •Упражнения
- •14. Регрессия и корреляция
- •14.1. Функциональная, статистическая и корреляционная зависимости
- •14.2. Линейная модель парной регрессии
- •14.3. Корреляционная таблица. Коэффициент корреляции
- •Упражнения
- •Домашняя контрольная работа
- •Библиографический список
- •Приложения. Математико-статистические таблицы

Пример 3.2. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины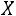 примера 3.1.
примера 3.1.
Решение. В соответствии с формулами (3.1) – (3.3) имеем
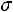

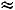

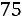
 ■
■
3.4. Функция распределения случайной величины
Определение. Функцией распределения случайной величины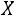 называется функция
называется функция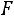
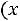
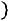 , определяемая соотношением
, определяемая соотношением
(3.4)
Пример 3.3. Найти функцию распределения для случайной величины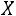 , определенной в примере 3.1.
, определенной в примере 3.1.
Решение. Рассмотрим различные значения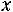

1) |
Если |
– |
|
, то |
|
||||
2) |
Если |
|
, то |
3)Если 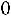
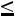


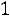 , то
, то

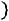


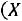


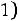
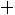
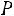
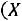

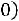

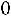


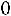
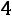

4)Если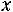
 , то
, то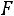
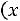


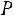
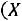


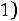
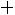
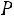
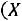


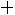
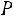


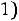

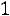
 Окончательно получаем следующее выражение для
Окончательно получаем следующее выражение для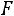

График этой функции показан на рисунке 3.1. ■
38
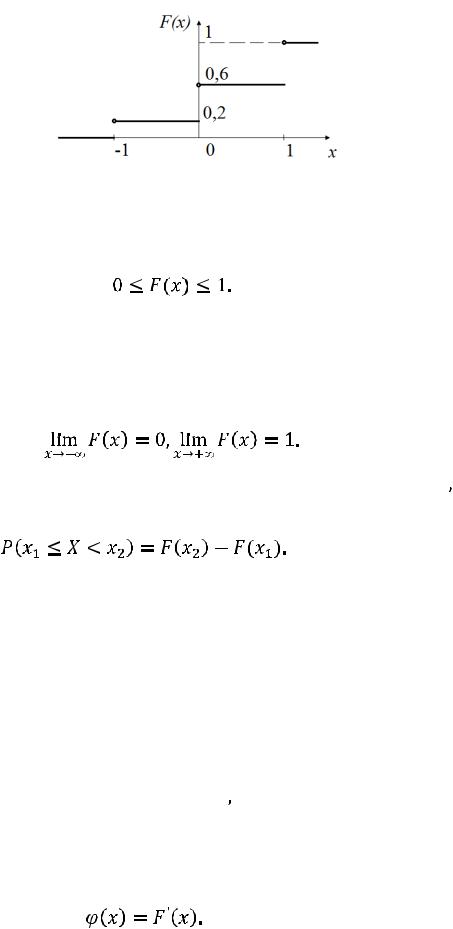
Рис. 3.1.
Рассмотрим свойства функции распределения.
1.Функция распределения принимает значения между 0 и 1:
2.Функция распределения – неубывающая функция.
3.На минус бесконечности функция распределения равна 0, на плюс бесконечности равна 1, т.е.
4.Вероятность попадания случайной величины в интервал 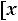
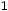

 равна приращению функции распределения на этом интервале, т.е.
равна приращению функции распределения на этом интервале, т.е.
(3.5)
3.5. Непрерывные случайные величины
Определение. Случайная величина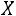 называется непрерывной, если функция распределения непрерывна во всех точках и дифференцируема всюду, кроме возможных отдельных точек.
называется непрерывной, если функция распределения непрерывна во всех точках и дифференцируема всюду, кроме возможных отдельных точек.
Теорема. Для непрерывных случайных величин вероятность попадания случайной величины в интервал 
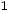

 не зависит от того, является этот интервал закрытым или открытым.
не зависит от того, является этот интервал закрытым или открытым.
Определение. Плотностью вероятности 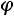
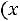
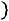 непрерывной случайной величины
непрерывной случайной величины называется производная ее функции распределения, т.е.
называется производная ее функции распределения, т.е.
(3.6)
39
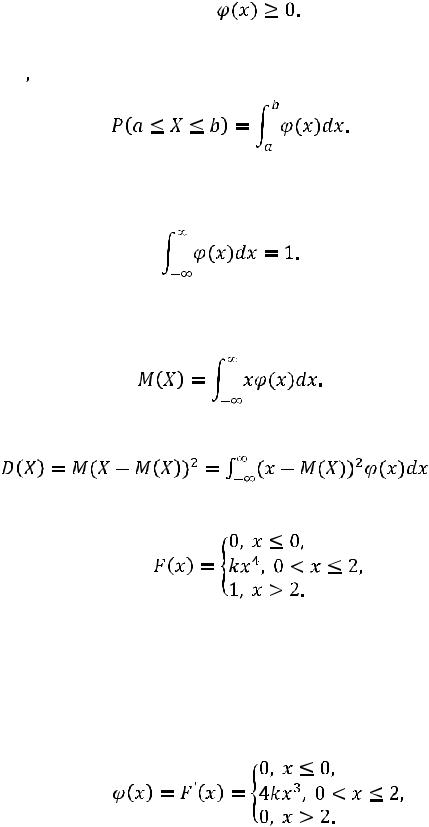
Отметим основные свойства функции 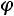


1.Плотность вероятности – неотрицательная функция, т.е.
2.Вероятность попадания непрерывной случайной величины в интервал 
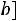 определяется по формуле
определяется по формуле
(3.7)
3. Несобственный интеграл в бесконечных пределах от плотности вероятности непрерывной случайной величины равен 1, т.е.
(3.8)
Определение. Математическое ожидание непрерывной случайной величины определяется следующей формулой:
(3.9)
Определение. Дисперсия может быть вычислена так:
. |
(3.10) |
Пример 3.4. Случайная величина задана функцией распределения
Требуется: а) определить параметр 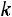 ; б) вычислить математическое ожидание и дисперсию; в) найти вероятность попадания случайной величины в интервал (0,1), показать данную вероятность на графиках функции распределения и плотности вероятности.
; б) вычислить математическое ожидание и дисперсию; в) найти вероятность попадания случайной величины в интервал (0,1), показать данную вероятность на графиках функции распределения и плотности вероятности.
Решение. а) Вычислим плотность вероятности по формуле (3.6):
Используя соотношение (3.8), будем иметь
40
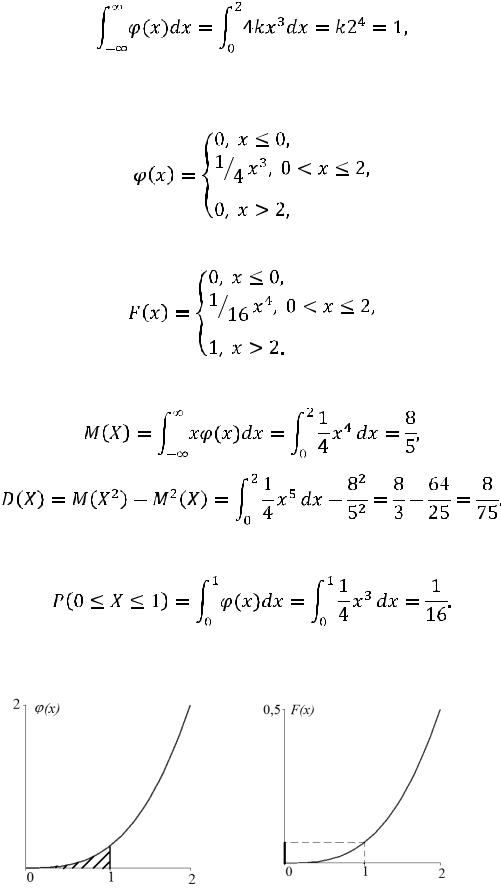
откуда находим, что 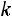

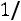
 Таким образом, плотность вероятности определяется так:
Таким образом, плотность вероятности определяется так:
а функция распределения определяется следующим образом:
б) По формулам (3.9), (3.10) находим
в) Используя формулу (3.7), будем иметь
Построим графики функций распределения (рис. 3.2) и плотности вероятности (рис. 3.3).
Рис. 3.2. Рис. 3.3.
41
