Для каждого варианта указанные десять строк таблицы дают 100 значений наблюдаемого признака.

Таблица 13.2

14.Регрессия и корреляция

14.1.Функциональная, статистическая и корреляционная зависимости

Определение. Функциональной зависимостью называется такая связь между переменными величинами, при которой зависимая величи- на-функция полностью определяется значениями влияющих независимых величин-аргументов. Вид зависимости между аргументами и функцией обычно задается в виде формулы, которая позволяет однозначно

100

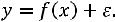
вычислить значение функции при подстановке аргумента в формулу.

Вэкономике функциональная зависимость между переменными проявляется редко. В экономике в большинстве случаев между переменными величинами существуют зависимости, когда каждому значению одной переменной соответствует не какое-то определенное, а множество возможных значений другой переменной. Иначе говоря, каждому значению одной переменной соответствует определенное (условное) распределение другой переменной. Такая зависимость получила название статистической (или стохастической, вероятностной). Примером статистической связи является зависимость урожайности от количества внесенных удобрений, производительности труда на предприятии от его энерговооруженности и т.п.

Если зависимость между двумя переменными такова, что каждому значению одной переменной соответствует определенное условное математическое ожидание (среднее значение) другой, то такая статистическая зависимость называется корреляционной. Иначе, корреляционной зависимостью между двумя переменными называется функциональная зависимость между значениями одной из них и условным математическим ожиданием другой.

Врегрессионном анализе рассматриваются односторонняя зависимость случайной переменной y от одной (или нескольких) неслучайной независимой переменной х. Такая зависимость может возникнуть, например, в случае, когда при каждом фиксированном значении х соответствующие значения y подвержены случайному разбросу за счет действия ряда неконтролируемых факторов.

Такая зависимость от х может быть представлена в виде модельного уравнения регрессии y по x:

(14.1)

При этом зависимую переменную y называют также результативным признаком, а независимую переменную x факторным признаком. График называется линией регрессии.

При определении корреляционной зависимости решаются две основные задачи:

101

Первая задача теории корреляции – установить форму корреляционной зависимости, то есть вид функции регрессии: линейная или нелинейная, т. е. квадратичная, показательная и т.д. Наиболее часто функции регрессии оказываются линейными. В этом случае корреляцию называют линейной, в противном случае − нелинейной.

Вторая задача теории корреляции − оценить тесноту (силу) корреляционной связи. Теснота корреляционной зависимости оценивается по величине рассеяния значений Y вокруг условного среднего .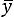

Большое рассеяние свидетельствует о слабой зависимости Y от Х либо об отсутствии зависимости. Малое рассеяние указывает на наличие достаточно сильной зависимости; возможно даже, что Y и Х связаны функционально, но под воздействием второстепенных случайных факторов эта связь оказалась размытой, в результате чего при одном и том же значении х величина y принимает различные значения.

14.2. Линейная модель парной регрессии

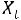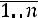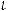
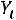
Пусть есть набор значений двух переменных и , . Можно отобразить пары 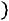точками на плоскости ХОY.

Рис. 14.1. Поле корреляции

Такое изображение статистической зависимости называется полем корреляции.

По расположению эмпирических точек можно предполагать наличие линейной корреляционной зависимости между переменными Х и Y. Поэтому уравнение регрессии будем искать в виде линейного уравнения

102

Это выборочное уравнение регрессии, а ее уравнение в генеральной совокупности имеет вид:

где 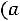– оценки параметров.

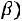Наличие случайного члена 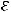(ошибки регрессии) связано с воздействием на зависимую переменную других неучтенных в уравнении факторов, с возможностью нелинейностью модели и ошибками измерения.

Для оценки параметров а и b используем систему нормальных уравнений:

14.3. Корреляционная таблица. Коэффициент корреляции

При большом числе наблюдений одно и то же значение х может

ные данные записывают в виде таблицы, которая называется корреляци-

онной таблицей.

Поясним устройство корреляционной таблицы на примере.

В первой строке таблицы указаны наблюдаемые значения (1, 2, 3, 4, 5) признака Х, а в первом столбце – наблюдаемые значения (28, 38,

103

48, 58) признака Y. На пересечении строк и столбцов находятся частоты 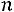наблюдаемых пар значений признаков. Например, частота 37 указывает, что пара чисел (4, 28) наблюдалась 37 раз. Черточка в клетке означает, что соответствующая пара чисел, например (1, 28), не наблюдалась. В последнем столбце записаны суммы частот строк, в последней строке – суммы частот столбцов. В клетке, расположенной в нижнем правом углу таблицы, помещена сумма всех частот (общее число всех наблюдений n).

Оценка силы линейной корреляционной зависимости может быть произведена при помощи коэффициента линейной корреляции:

(14.5)

(14.6)

Уравнение линейной регрессии при этом можно представить в виде:

Величина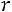 является показателем тесноты связи и называется выборочным коэффициентом корреляции (или просто коэффициентом корреляции).

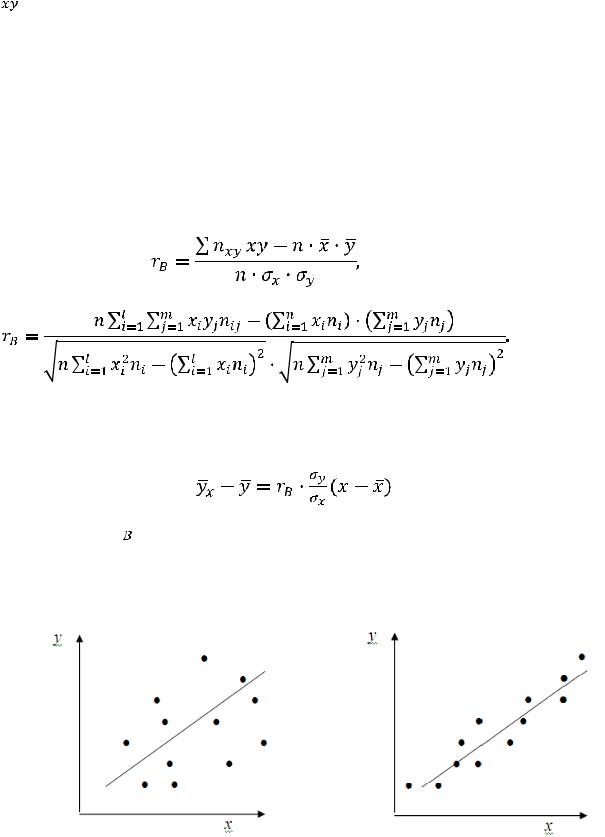
Приведем двапримеракорреляционных зависимостей переменныхY отX.

Рис. 14.2. Корреляционная зависимость

104

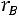
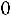
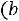
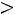
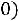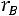
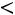
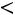
Если , то корреляционная связь между переменными называется прямой, если 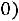– обратной. При прямой (обратной) связи увеличение одной из переменных ведет к увеличению (уменьшению) условной (групповой) средней другой.

Выборочный коэффициент корреляции обладает следующими свойствами:

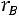
1.Коэффициент корреляции принимает значение на отрезке [–1; 1]. Чем ближе к единице, тем теснее связь.

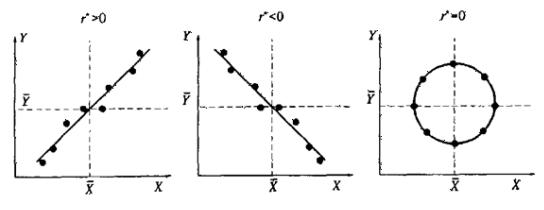
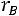
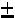
2.При корреляционная связь представляет линейную функциональную зависимость. При этом все наблюдаемые значения располагаются на прямой линии.

3.При 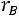линейная корреляционная связь отсутствует. При этом линия регрессии параллельна оси ОХ.

Рис. 14.3. Типы зависимостей и коэффициент корреляции

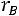
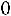
Шкала оценки зависимостей позволяет разграничить связь между факторными и результативными признаками на устойчивую и неустойчивую. Наличие устойчивой связи свидетельствует о достоверности параметров уравнений зависимости, что дает возможность использовать их при проведении нормативных и прогнозных расчетов. 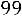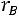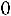Например, если величина, что достаточно близко к 1 и означает наличие очень тесной зависимости результата от фактора, 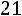– связь очень низкая, обратная.

Пример 14.1. Результаты наблюдений за двумя признаками и 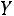представлены в виде таблицы:

Требуется:

1.Вычислить коэффициент корреляции 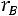и сделать вывод о линейной корреляционной связи между 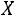и .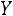

2.Найти уравнение линейной регрессии.

106