Пример 1.8. В партии из 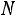имеется 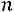стандартных. Наудачу ото-

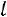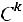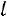
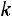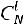
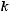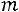
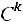
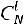
Происходит сложное событие: из деталей должно быть стандартных (стандартные детали можно отобрать только из стандартных, число способов отбора равно ) и нестандартных (неcтандартные детали можно отобрать только из нестандартных, число способов отбора равно ). В итоге имеем число благоприятствующих исходов: 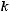. Общее число исходов равно числу способов выбора из 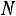дета-

лей 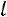деталей: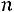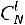. Тогда искомая вероятность равна: ■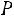

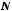
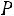
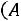
Система вероятностей, задаваемая формулой 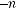, называ-

ется гипергеометрическим распределением.

1.4. Условная вероятность события

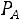
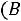
Обозначим через условную вероятность события 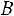, найденную в предположении, что событие 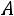произошло.

Теорема (произведение вероятностей). Вероятность произведения двух событий равна вероятности произведения одного из них на условную вероятность второго, найденную при условии, что первое уже произошло:

(1.10)

Пример 1.9. Из колоды в 36 карт наудачу вынимают две карты. Найти вероятность того, что на второй карте будет туз при условии, что первым вынули туза.

Решение. Обозначим через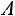 событие, состоящее в том, что первой вынутой картой оказался туз, через 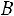событие, состоящее в том, что

12

вторым тоже оказался туз. Тогда событие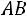 состоит в выпадении двух тузов, вероятность этого события надо найти.

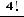
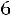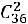
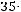
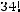
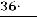
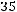
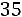
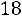
Найдем вероятность по формуле (1.3). Два туза из имеющихся в колоде четырех тузов можно вытащить способами. Две карты из 36 можно вытащить 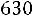способами. Поэтому

Вычислим теперь искомую вероятность по формуле (1.8). Заметим,

что

Если событие 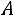произошло, то в колоде осталось 35 карт и среди них только 3 туза. Поэтому

В соответствии с формулой (1.8) будем иметь

Таким образом, получили, что решения, найденные по формулам

(1.3) и (1.10), совпадают. ■

Формула (1.10) может быть обобщена на случай произвольного числа событий:

(1.11)

Пример 1.10. На карточках написаны буквы М, М, А, А. Карточки наудачу раскладываются одна за другой. Найти вероятность того, что получится слово МАМА.

Решение. Обозначим через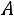 событие, состоящее в том, что получено слово МАМА, через 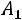– буква М на первом месте, – буква А на втором месте, – буква М на третьем месте, – буква А на четвертом месте.

13

Используя операции с событиями, получаем

В соответствии с формулой (1.1) будем иметь

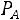
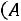
Поясним вычисление, например, множителя 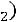. В данном случае предполагается, что событие произошло. Поэтому осталось 3 карточки с буквами М, А, А. Поэтому вероятность того, что следующей достанут карточку с буквой А, равняется . ■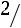

Определение. События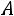 и называются независимыми, если вероятность наступления одного из них не зависит от того, произошло второе событие или нет, т.е. (ср. с (1.8))

купности, если независимы любые два из них и независимы любое из них и произведения остальных событий. В противном случае события зависимы.

Замечание. Известный пример С.Н. Бернштейна [10] показывает, что попарная независимость нескольких событий не означает независимости событий в совокупности. ■

Для независимых событий формулы (1.10), (1.11) принимают вид

,

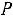
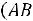
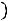
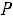
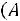
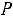
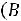
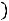(1.12)

1.5. Вероятность суммы двух событий

В предыдущем подразделе было отмечено, что при вычислении вероятности произведения событий необходимо знать о зависимости или

14

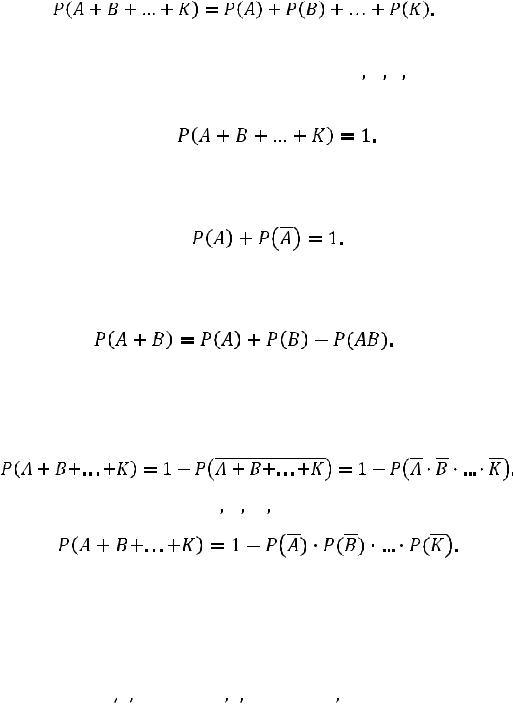
независимости событий. В данном подразделе покажем, что для вычисления вероятности суммы двух событий важно понимать, являются ли суммируемые события совместными.

Теорема. Вероятность суммы конечного числа несовместных событий равна сумме вероятностей этих событий, т.е.

(1.13)

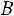
Следствие 1. Сумма вероятностей событий, образующих полную группу, равна единице, т.е. если события 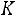образуют полную группу, то

Следствие 2. Сумма вероятностей противоположных событий равна единице:

(1.14)

Теорема. Вероятность суммы двух совместных событий равна сумме вероятностей этих событий без вероятности их произведения, т.е.

(1.15)

В случае трех и более событий вместо обобщения формулы (1.13) рассматривают переход к противоположному событию следующим образом:

(1.16)

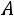
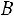
Если при этом события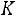независимы, то

(1.17)

Пример 1.11. Три стрелка независимо друг от друга производят по выстрелу в мишень. Вероятности попадания равны 0,6, 0,7, 0,8. Найти вероятность того, что в мишень попадет хотя бы один стрелок.

Решение. Пусть событие – попадание i-го стрелка. По условию задачи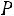

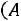
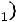
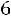
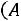
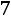
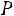
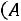
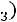
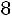
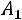
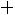
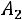
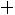
С учетом наших обозначений требуется определить вероятность суммы 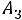. События 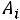совместны и независимы, поэтому в соответствии с формулой (1.15) имеем

15