2. Случайная величина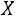 задана плотностью вероятности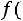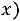, которая принимает значения 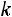на отрезках [a1,1+a1+a2] и [2+a1+a2+a3, 3+a1+a2+a3+a4], а вне этих отрезков равно 0. Найти: а) значение 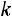, при котором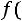 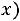будет плотностью вероятности, б) математическое ожидание и дисперсию этой случайной величины.

4.Основные законы распределения

4.1.Биномиальное распределение

Определение. Дискретная случайная величина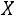 имеет биномиальный закон распределения с параметрами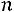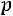, если она принимает значения 0, 1, 2, …,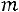, …, 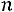с вероятностями

(4.1)

где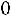

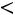
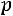
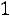
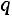
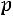
Теорема. Математическое ожидание и дисперсия случайной величины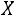, распределенной по биномиальному закону, находятся так:

(4.2)

Пример 4.1. Считая, что вероятности рождения мальчиков и девочек одинаковы, составить закон распределения числа мальчиков в семье с двумя детьми.

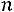
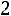
Решение. В данном случае число мальчиков распределено по биномиальному закону с параметрами. Возможное количество мальчиков – 0, 1, 2. Соответствующие вероятности находим следующим образом:

Таким образом, закон распределения имеет вид

46

0,25 0,5 0,25

4.2. Закон распределения Пуассона

Определение. Дискретная случайная величина 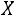имеет закон распределения Пуассона с параметром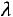, если она принимает значения 0, 1, 2, …,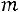, … с вероятностями

(4.3)

Теорема. Математическое ожидание и дисперсия случайной величины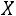, распределенной по закону Пуассона, равны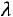, т.е.

(4.4)

4.3. Равномерный закон распределения

Определение. Непрерывная случайная величина имеет равномерный закон распределения на отрезке 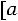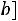, если ее плотность вероятности определяется соотношением

(4.5)

Теорема. Функция распределения случайной величины, распределенной по равномерному закону, имеет вид

(4.6)

Теорема. Математическое ожидание и дисперсия случайной величины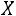, распределенной по равномерному закону, определяются так:

47

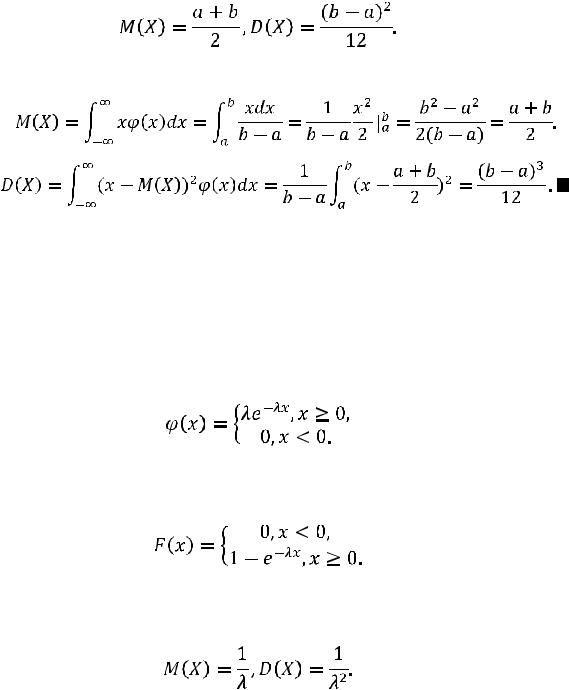
(4.7)

Доказательство. В соответствии с формулами (3.9), (3.10) имеем

4.4. Показательный закон распределения

Определение. Непрерывная случайная величина 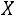имеет показа-

тельный (экспоненциальный) закон распределения с параметром

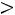
, если ее плотность вероятности определяется соотношением

(4.8)

Теорема. Функция распределения случайной величины, распределенной по показательному закону, имеет вид

(4.9)

Теорема. Математическое ожидание и дисперсия случайной величины, распределенной по показательному закону, определяются так:

(4.10)

4.5. Нормальный закон распределения

Определение. Непрерывная случайная величина имеет нормаль-

ный закон распределения (закон Гаусса) с параметрам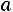и и 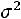, если ее плотность вероятности определяется соотношением

48

(4.11)

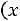
Характерный график плотности вероятности приведен на рис. 4.1.

Теорема. Функция распределения случайной величины, распределенной

по нормальному закону, имеет вид

Рис. 4.1.

(4.12)

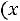
где – функция Лапласса (см. (2.5)).

Теорема. Математическое ожидание и дисперсия случайной величины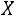, распределенной по нормальному закону, определяются так:

(4.13)

Свойства случайной величины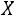, распределенной по нормальному закону:

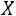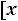
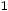
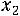
1. Вероятность попадания случайной величины в интервал равна

(4.14)

где

2. Вероятность того, что отклонение случайной величины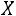 от математического ожидания 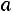не превосходит величину 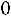по абсолютной величине, равна

(4.15)

где .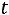

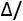
49