4.6.Коробки с конфетами упаковываются автоматически. Их средняя масса равна 540 г. Известно, что масса коробок с конфетами имеет нормальное распределение, а 5 % коробок имеют массу, меньшую 500 г. Каков процент коробок, масса которых: а) менее 470 г; б) от 500 до 550 г; в) более 550 г; г) отличается от средней не более чем на 30 г (по абс о-

лютной величине)? Ответ: а) 0,05; б) 0,609; в) 0,341; г) 0,781.

4.7.Имеется случайная величина X , распределенная по нормаль-

ному закону с математическим ожиданием а и дисперсией σ 2 . Требуется приближенно заменить нормальный закон распределения равномерным законом в интервале (α ; β ); границы α , β подобрать так, чтобы сохранить неизменными математическое ожидание и дисперсию случайной величины X . Ответ: ; .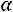

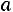
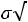
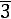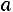
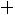
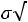
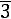Контрольная работа по разделу 4

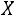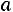
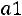
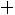
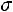
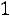
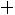
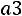
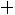
1.Случайная величина имеет нормальный закон распределения с параметрами 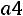. Необходимо: 1) найти и п о- строить графики плотности вероятности и функции распределения;

2)определить вероятность попадания случайной величины в интервал (2,5); 3) сформулировать «правило трех сигм».

5.Закон больших чисел и предельные теоремы

5.1.Неравенство Маркова

Теорема. Если случайная величина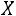 принимает только неотрицательные значения и имеет математическое ожидание, то для любого положительного числа 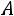выполняется неравенство

(5.1)

Следствие.

(5.2)

51

Пример 5.1. Среднее количество вызовов, поступающих на коммутатор завода в течение часа, равно 300. Оценить вероятность того, что в течение следующего часа число вызовов на коммутатор: а) превысит

5.2. Неравенство Чебышева

Теорема. Для любой случайной величины, имеющей математическое ожидание и дисперсию, справедливо неравенство Чебышева:

тивоположны, неравенство (5.3) можно записать в следующем виде:

(5.4)

Следствие 2. Если случайная величина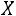 распределена по биномиальному закону, то выражение (5.4) принимает вид

(5.5)

Пример 5.2. Вероятность выхода с автомата стандартной детали равна 0,96. Оцените с помощью неравенства Чебышева вероятность того, что число бракованных среди 2000 деталей находится в границах от 60 до 100 включительно. Уточните вероятность того же события с помощью интегральной формулы Муавра-Лапласа. Объясните полученные результаты.

52

Поэтому в соответствии с неравенством (5.5) получаем

Применяя интегральную формулу Муавра-Лапласа (2.5), имеем

Различие результатов объясняется тем, что неравенство Чебышева дает оценку вероятности для любой случайной величины, а интегральная формула Муавра-Лапласа дает более точное значение именно для биномиального распределения, которое рассмотрено в данном примере. ■

5.3. Теорема Чебышева

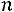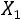
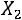
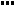
Если дисперсии независимых случайных величин 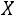ограничены постоянной 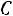, то при неограниченном увеличении числа 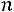средняя арифметическая случайных величин сходится по вероятности к средней арифметической их математических ожиданий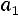 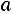, т.е.

(5.6)

Для практических расчетов удобно использовать неравенство [10]

(5.7)

53

Пример 5.3. Сколько надо провести измерений данной величины, чтобы с вероятностью не менее 0,95 гарантировать отклонение средней арифметической этих измерений от истинного значения величины не более чем на 1 по абсолютной величине, если среднее квадратическое отклонение каждого из измерений не превосходит 5?

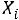
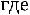
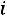
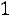
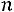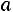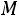
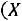
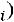
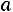
Решение. Обозначим через результат i-го измерения. Пусть – истинное значение, тогда Требуется найти значение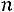, при котором будет выполняться неравенство

В соответствии с (5.7) это неравенство выполняется при

Решая последнее равенство, получаем

■

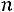
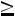
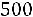
5.4. Центральная предельная теорема

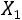
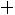
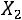
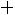
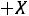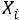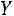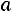
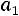
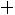
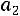
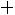
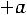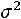
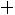
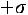
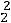
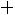
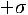
Если представляет собой сумму достаточно большого числа независимых случайных величин, при этом влияние каждой из случайных величин на всю сумму мало, то закон распределения близок к нормальному с параметрами , , 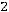где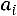

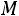
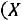
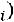
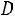
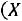
Таким образом, получаем, что при определенных условиях совокупное действие случайных величин приводит к нормальному закону распределения, в этом и состоит его особая роль.

Пример 5.4. Пусть в некотором учебном заведении вероятность получения студентом оценки «2» по высшей математике составляет 0,3, оценки «3» – 0,3, оценки «4» – 0,3, оценки «5» – 0,1. Составить закон распределения случайной величины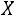 – суммы оценок для группы из 20

54