3. Понятие о случайных событиях и случайных величинах
До сих пор мы рассматривали случайные события. В какой-то мере они подобны точке на оси, то есть никакого измерения не имеют. Но в практике есть целый ряд величин, связанных со случайными событиями, и тем не менее таковыми не являющимися. Если у рассмотренных выше лампочек измерить время работы от ее начала до перегорания (отказа), то мы получим какую-то величину (время или наработку), которая у каждой отдельно взятой лампочки будет своей. Так как на работу лампочки влияет огромное количество факторов, то предсказать время ее работы до отказа заранее невозможно. Такие величины называются случайными величинами. В Теории надежности это, как правило, – время работы (или наработка) до отказа. Можно сказать, что Теория надежности изучает главным образом эту случайную величину.
Случайной величиной называется величина, которая в результате испытаний может принимать то или иное значение. При этом подразумевается, что само это значение будет непременно, то есть событие, до которого эта величина измеряется, случится обязательно.
Случайные величины бывают дискретные и непрерывные, последние встречаются гораздо чаще, например, наработка до отказа различных устройств, время вынужденного простоя из-за отказов, токи фидеров и вводов подстанций, напряжения на шинах подстанций и на токоприемниках ЭПС и многие другие. Для дискретной случайной величины можно перечислить все возможные значения, можно их перенумеровать.
Если до опыта точно определить случайную величину невозможно, то наблюдая за работой некоторой партии изделий, можно вывести какие-то объективные закономерности в поведении случайных величин. Эти закономерности описываются с помощью вероятностных характеристик распределения. В этих характеристиках используется не вероятность точного значения случайной величины, а вероятность непревышения данной случайной величиной какого-то заданного, неслучайного значения. Например, для случайной величины Т такая характеристика будет вероятностью
F(t) = p{T < t}.
Эта характеристика называется интегральной функцией распределения случайной величины Т. Как у всякой вероятности минимальное значение функцииF(t) равно нулю, а максимальное – единице. Функция распределения – неубывающая функция времени.
Пользоваться интегральной функцией распределения неудобно, поэтому гораздо чаще используется не сама эта функция, а ее производная по времени – плотность распределения случайной величины
d[F(t)]
f(t)=F′(t) = ------------
dt
Зная плотность распределения случайной величины, можно получить интегральную функцию распределения
t
F(t)= ∫f(t)dt.
0
Имея функцию распределения непрерывной случайной величины, можно определить вероятность ее попадания в заданный интервал
b
p{а < T < b} = ∫f(t)dt
a
Функция и плотность распределения представлены на рисунке 3.
Это были так называемые полные характеристики случайной величины. Кроме них есть еще числовые характеристики. Главная из них – математичес-кое ожидание М[Т]. Если мы характеризуем какую-то случайную величину на основании статистических данных, то мы получим статистическую оценку математического ожидания – среднее значение. В теории надежности она имеет специальное название – средняя наработка до отказа (СНДО).
f(t),
F(t)
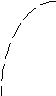
1
f(t)=F′(t)
q(t) = F(t)
T
Рис. 3