Вероятность имеет смысл только в связи с данной информацией. Безотносительной, «истинной» вероятности какого-либо происходящего события не существует.

2. Основные законы теории вероятностей

Говоря о законах Теории вероятностей, необходимо освежить понятия конъюнкции событий и их дизъюнкции. Если событие С является дизъюнкцией событийАиВ, то оно произойдет тогда, когда произойдет хотя бы одно из событийАилиВ(или оба вместе). Если же событие D является конъюнкцией этих событий, то оно произойдет только тогда, когда эти события случатся одновременно и ни в каком другом случае событие Dне наступит. События С и D называются сложными событиями.

Например, обрыв гирлянды изоляторов произойдет в случае разрыва любого из изоляторов, то есть отказ гирлянды есть дизъюнкция отказов составляющих ее изоляторов.

Если рассматривать всю изоляцию участка контактной сети, то ее отказ (пробой) есть дизъюнкция отказов отдельных гирлянд, так как при пробое любой из них контактная сеть не сможет держать рабочее напряжение, а это – ее отказ. Наоборот, безотказная работа изоляции контактной сети – конъюнкция безотказных работ всех гирлянд данного участка.

Студентам-электрикам может быть полезной релейно-контактная аналогия этих понятий. Рассмотрим рисунок 1.

Нетрудно убедиться, что ток через обмотку реле D будет протекать при замыкании любого из контактов А или B, тогда как для запитки реле С необходимо одновременное замыкание обоих контактов – и реле А, и реле B.

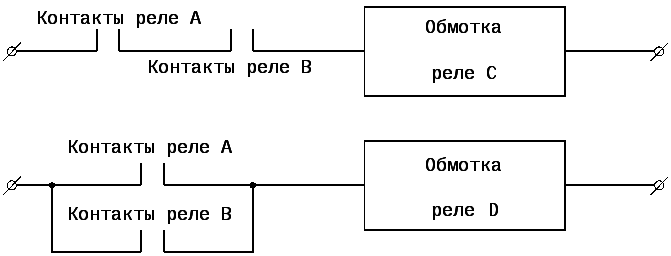
Рис. 1

Релейно-контактная аналогия дизъюнкции и конъюнкции

Рассмотрим вероятность сложного события С, являющегося конъюнкцией двух простых событий А и В. Вероятность сложного события С = А В, определяется произведением вероятности события А при условии события В - р(А/В) и вероятности самого события В - р(В) или произведением вероятности события В при условии события А - р(В/А) и вероятности самого события А - р(А).

р(С) = р(А В) = р(А/В) р(В) = р(В/А) р(А) . (3)

Если события А и В не зависят друг от друга, то выражение р(А/В) превратится в безусловную вероятность события А, а выражение р(В/А) - в безусловную вероятность события В и вероятность события С определится

р(С) = р(А) р(В) = р(В) р(А) . (4)

Задача 1.Какова вероятность того, что на выборах президента США в 1992 году был бы избран левша, если тогда впервые в истории этой страны в бюллетенях присутствовали не два, а три кандидата (Дж. Буш-старший, Билл Клинтон и Рос Перо)? По статистике каждый десятый мужчина, родившийся в США, является левшой. Если все три кандидата уже являются левшами, то тогда с вероятностью, равной единице, президентом страны будет избран левша. Так как никто из кандидатов не состоит в родстве друг с другом, рассматриваемые события следует считать не зависящими друг от друга, и вероятность того, что все три кандидата в президенты являются левшами, определяем по выражению (4)

р = р(А₁) р(А₂) р(А₃) = 0,1 0,1 0,1 = 0,001.

Некоторые студенты, ничего не решая, сразу же заявляют, что эта вероятность равна единице, так как иначе не было бы самой этой задачи. Следует признать, что в данном случае это утверждение является истинным, и все три перечисленных политических деятеля действительно левши!

Раньше уже говорилось, что вероятность извлечения из колоды туза равна 4/52. Мы здесь сложили четыре равных вероятности появления одного туза, так как их в колоде четыре. В данном случае результат верен, но всегда ли вероятности можно суммировать?

Задача 2. Чему равна вероятность того, что из двух наугад взятых из ящика лампочек хотя бы одна исправна, если известно, что вероятность безотказной работы (ВБР) таких лампочек равна 0,6? Сложение вероятностей даст результат больше единицы, что противоречит здравому смыслу. Как же определить эту вероятность и почему в случае с тузами ответ был правильным?

Извлекая карты из колоды, мы никак не могли в одном и том же опыте получить два разных туза, а в случае с лампочками это вполне возможно – обе лампочки могут оказаться исправными.

Если сложное событие С заключается в появлении хотя бы одного из событий А или В, а одновременно они произойти не могут, то вероятность события С равна сумме вероятностей событий А и В.

р(С) = р(А) + р(В). (5)

В этом случае события имеют специальное название. Если события вместе наступить не могут, то они называются несовместными. Извлечение из колоды тузов – группа несовместных событий, так как одна карта никак не может быть сразу несколькими тузами. Если мы перебрали все возможные варианты несовместных событий, то одно их них случится непременно. Такая группа событий называется полной группой несовместных событий. Вероятность того, что случится одно из этих событий, равна единице.

n

р(С) = р(С₁) + р(С₂) ...+ … р(С_i) ...+ … р(С_n) =  р(С_i) = 1. (6)

i=1

Самый простой пример такой группы событий – противоположные события

А и Ā. Очевидно, что одно из них случится непременно и

р(А +Ā) = р(А) + р(Ā) = 1. (7)

Вероятность полной группы несовместных событий - достоверное событие.

Остался нерешенным вопрос – как же рассчитать вероятность суммы совместныхсобытий?

Вернёмся к Задаче 2.В этом случае самое простое решение – воспользоваться уже имеющимися знаниями и расписать все возможные события, составив полную группунесовместныхсобытий. Здесь она будет состоять из четырёх событий:

1) Первая лампочка исправна, вторая – нет;

2) Первая лампочка неисправна, вторая исправна;

3) Обе лампочки исправны;

4) Обе лампочки неисправны.

Эти сложные события, состоящие из событий, независимых друг от друга. Вероятности каждого из этих сложных событий определяются по формуле (4).

р(Соб₁) = р₁ q₂ ,

где р₁ – вероятность исправности первой лампочки, равная 0,6;

q₂ – вероятность неисправности второй лампочки, равная 0,4;

р(Соб₁) = 0,6 0,4 = 0,24.

Вероятность второго события

р(Соб₂) = q₁ р₂ = 0,4 0,6 = 0,24,

так как лампочки одинаковые.

Вероятность третьего события – одновременной исправности лампочек

р(Соб₃) = р₁ р₂ = 0,6 0,6 = 0,36.

Наша искомая вероятность равна сумме этих трех вероятностей, так как заданное условие – исправность хотя бы одной лампочки – выполняется при любом из этих трёх событий.

р = р(Соб₁) + р(Соб₂) + р(Соб₃) = 0,24 + 0,24 + 0,36 = 0,84.

А если бы по условию задачи определялась вероятность исправности одной лампочки из четырёх наугад взятых из ящика? Составить полную группу несовместных событий было бы значительно сложнее, и вычислений было бы намного больше.

Ответ в обоих вариантах задачи можно получить иначе. Приведенные четыре события в первом варианте являются полной группой несовместных событий и сумма их вероятностей равна единице. Иногда бывает проще рассчитать вероятность события противоположного заданному, и искомую вероятность получить, вычитая этот результат из единицы. В первом варианте задачи противоположное событие одно – последнее из четырех – обе лампочки неисправны. Его вероятность

р(Соб₄) = q₁ q ₂ = 0,4 0,4 = 0,16.