2) пронормируем l величиной lо , для чего умножим и разделим правую часть

уравнения на lо . Путем соответствующего группирования членов перейдем к относительным управляющим воздействиям:

Подставив (1.8) и (1.9) в (1.7), получим дифференциальное линеаризованное уравнение в относительных величинах, связывающее относительные угловую скорость

Коэффициент T называется постоянной времени двигателя (объекта регулирования) и имеет размерность времени (с). Он определяет быстродействие двигателя, т.е. как быстро устанавливается заданная угловая скорость при изменении управляющего воздействия.

Коэффициент k носит название передаточного коэффициента и является безразмерной величиной. Он характеризует зависимость между изменением выходной

величины x(t) и управляющим воздействием z(t) в установившемся режиме. Следует подчеркнуть, что дифференциальное уравнение (1.10) описывает

динамику линеаризованной системы управления двигателем в окрестности рабочей

точки ( wо , lо ). Если в исходной нелинейной системе (1.1) изменится рабочая точка, то

это вызовет изменение коэффициентов T и k .

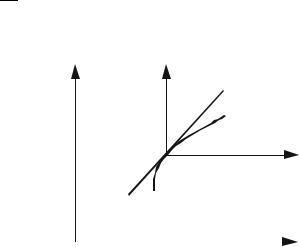
Рассмотрим геометрический смысл линеаризации (рис.1.16). Линеаризация нелинейной зависимости двух переменных означает:

∙замену исходной кривой AB отрезком ее касательной A'B' в точке O′ , соответствующей установившемуся режиму;

∙параллельный перенос начала координат в точку O′ .

1.6. Частотные характеристики линейных динамических систем

22

В дальнейшем будем рассматривать стационарные линейные динамические системы (ЛДС), т.е. системы, которые представляются следующим дифференциальным уравнением:

p = dpd - оператор дифференцирования.

Mc Mc

B

B

O Δω

A A

Рис.1.16.Графическая интерпретация процесса

линеаризации динамической системы

Для математического описания ЛДС широко используются частотные характеристики, позволяющие судить о реакции системы на входные гармонические воздействия различных частот.

Пусть на вход ЛДС поступает гармоническое воздействие в виде бесконечной косинусоиды: z(t) = Z cos(ωt) . Определим x(t) - реакцию системы на этот сигнал.

Для всех ЛДС справедлив принцип суперпозиции: реакция системы на

несколько одновременных входных воздействий равна сумме реакций на каждое воздействие (рис.1.17).

23

Рис.1.17. К пояснению принципа суперпозиции

Отсюда следует практический вывод: если на вход ЛДС поступает сложный сигнал, который можно представить в виде совокупности нескольких простых сигналов

zi (t) , то результирующим сигналом на выходе системы будет сумма реакций этой системы на каждую составляющую xi (t) .

раскладывается входной сигнал z(t) . Для частного случая, когда входной сигнал имеет

вид z(t) = z1(t) + z2 (t) , выходной сигнал вычисляется по формуле: xi (t) = x1(t) + x2 (t) . Определим эффекты, создаваемые каждым из двух экспоненциальных воздействий, на которые разложен исходный входной сигнал.

Для ЛДС справедливо следующее правило: реакцию системы на входное

воздействие можно вычислить путем умножения этого сигнала на функцию параметров системы:

x1(t) = z1(t)W ,

где W - некоторая функция параметров системы. Например, для радиоэлектронной системы функция W зависит от номиналов резисторов, конденсаторов, индуктивностей, составляющих данную систему. При этом для стационарной системы W не является функцией времени (W ¹ W(t)).

После подстановки выражений для входного и выходного сигналов и их производных в дифференциальное уравнение (1.11) получим:

24

причем для реальных динамических систем m ≤ n .

Если в числителе и знаменателе раскрыть скобки, то получим:

W ( jω) = A(ω) + jB(ω) C(ω) + jD(ω) ,

где A(ω) = bо − b2 ω2 + b4 ω4 − b6 ω6 + ...; B(ω) = b1ω − b3ω3 + b5ω5...; C(ω) = aо − a2ω2 + a4ω4 − a6ω6 + ...; D(ω) = a1ω − a3ω3 + a5ω5...,

причем A(ω) и C(ω) - четные функции; B(ω) и D(ω) - нечетные.

W ( jω) носит название амплитудно-фазовой частотной характеристики или просто амплитудно-фазовой характеристики (АФХ), иногда ее называют комплексной

частотной характеристикой (КЧХ). Неправильно называть W ( jω) передаточной функцией, так как данный термин закреплен в ТАУ за другим важным понятием.

С целью упрощения записи формул введем обозначения: A = A(ω) ; B = В(ω) ; C = C(ω) ; D = D(ω). Тогда имеем:

где U (ω) = Re[W ( jω)] - вещественная частотная характеристика ЛДС; V (ω) = Im[W ( jω)] - мнимая частотная характеристика.

Функция U (ω) является четной в силу того, что

U (−ω) = Re[W (− jω)]= Re[W ( jω)]= U (ω) .

Здесь используются следующие соотношения:

∙произведение двух четных функций является четной функцией;

∙произведение двух нечетных функций является четной функцией;

∙произведение нечетной и четной функции дает нечетную функцию.

Функция V (ω) - нечетная, так как

V (−ω) = Im[W (− jω)]= − Im[W ( jω)]= −V (ω) .

В полярных координатах на комплексной плоскости АФХ имеет:

W ( jω) = H (ω)e jϕ(ω).

Величина H (ω) называется амплитудно-частотной характеристикой (АЧХ) и

квадранты). Формулы для вычисления ϕ(ω) для различных квадрантов представлены на рис.1.18.

25

Рис.1.18. К определению ФЧХ в зависимости от номера

квадранта

Функция ϕ(ω) является нечетной, так как ϕ(ω) = −ϕ(−ω) .

На комплексной плоскости АФХ определяет вектор, модуль которого равен

аргумент ϕ(ω) - угол, образованный этим вектором с действительной положительной полуосью.

Кривая, которую прочерчивает конец вектора W ( jω) при изменении ω от 0 до +∞ (иногда от –∞ до +∞), называется годографом, или АФХ системы (рис.1.19).

jV(ω)

Рис.1.19. Годограф динамической системы

Ранее было показано, что вещественная частотная характеристика является четной функцией, а мнимая частотная характеристика - нечетной функцией частоты. В

силу этого годограф, построенный для положительных значений ω , является зеркальным

отображением годографа, построенного для отрицательных значений ω .

Таким образом, ЛДС могут представлять пять частотных характеристик, между которыми существуют следующие очевидные зависимости:

1) АФХ или КЧХ

2) вещественная частотная характеристика

U (ω) = H (ω)cosϕ(ω) ; 3) мнимая частотная характеристика

26

= ZH (ω) e j[ωt +ϕ(ω)] + e− j[ωt +ϕ(ω)] = ZH (ω) cos[ωt + ϕ(t)]. 2

Можно сделать следующий вывод: если на вход ЛДС подать гармонический сигнал определенной частоты и определенной амплитуды, то на выходе также получим

гармонический сигнал той же частоты, но его амплитуда изменится в H (ω) раз и выходной сигнал сдвинется по фазе на угол ϕ(ω) .

Графики входного z(t) и выходного x(t) сигналов представлены на рис.1.20.

27