
- •Введение
- •1.2. Принципы автоматического управления
- •1.3. Классификация математических моделей динамических систем
- •1.4. Типовые входные воздействия, их представление во временной и комплексной областях, практическое применение
- •1.6. Частотные характеристики линейных динамических систем
- •1.7. Экспериментальное определение частотных характеристик линейной динамической системы
- •1.8. Передаточная функция линейной динамической системы и ее свойства
- •2.1. Общая характеристика типовых звеньев и их классификация
- •2.2. Апериодическое звено
- •2.4. Дифференцирующее звено первого порядка
- •2.5. Безынерционное звено
- •2.6. Интегрирующее звено
- •2.7. Идеальное дифференцирующее звено
- •2.8. Колебательное звено
- •2.9. Дифференцирующее звено второго порядка
- •2.10. Запаздывающее звено
- •2.12. Методика построения ЛЧХ сложных САУ
- •Глава 3. Структурные схемы и передаточные функции автоматических систем
- •3.2. Функциональная схема замкнутой САУ, назначение отдельных устройств и элементов. Классификация САУ
- •3.4. Правила преобразования структурных схем
- •3.5. Примеры преобразования структурной схемы сложной динамической системы
- •Глава 4. Устойчивость систем автоматического управления
- •4.1. Понятие устойчивости. Устойчивость и корни характеристического уравнения
- •4.2. Алгебраический критерий устойчивости Рауса – Гурвица
- •4.3. Критерий устойчивости Михайлова
- •4.4. Следствия из критерия Михайлова
- •4.5. Критерий устойчивости Найквиста
- •4.6. Применение критерия устойчивости Найквиста для астатических систем
- •4.7. Логарифмический критерий устойчивости
- •4.8. Запасы устойчивости по амплитуде и фазе
- •Литература

5)дает возможность использовать частотные характеристики разомкнутых систем, полученные при анализе устойчивости, и на других этапах исследования САУ (при анализе качества регулирования, для построения частотных характеристик замкнутых систем).
4.6.Применение критерия устойчивости Найквиста для астатических систем
АФХ статических систем при изменении частоты от 0 до +∞ образуют |
||
замкнутый контур (рис.4.24). Для устойчивых систем он начинается на вещественной |
||
оси в точке (k; 0) . Сдвиг фаз изменяется в пределах от ϕ = 0 |
при ω = 0 до ϕ = −nπ / 2 , где |
|
n - порядок системы при ω → ∞ . |
|
|
Im |
|
|
ω |
ω = 0 |
|
|
|
|
0 |
Re |
|
|
W (jω) |
|
Рис.4.24. График АФХ статической |
||
системы третьего порядка |
|
|
Астатические системы содержат интегрирующие звенья. Поэтому их
передаточные функции имеют полюс s = 0, |
находящийся на границе левой и правой |
|||||||||||
полуплоскостей корней (т.е. разомкнутая система нейтрально-устойчивая). |
||||||||||||
АФХ разомкнутой астатической системы может быть представлена в |
||||||||||||
следующем виде: |
|
|
|
|
|
|
|
kW0 ( jω) |
|
|||
W ( jω) = W(s) |
|
s= jω = |
R(s) |
|
= |
kW0 (s) |
|
|
= |
, |
||
|
|
|
||||||||||
|
|
|||||||||||
|
Q(s) |
|
sγ |
|
|
s= jω |
( jω)γ |
|||||
|
|
s= jω |
(4.31) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|||
где γ - порядок астатизма системы. Будем полагать, что W0 (s) не имеет полюсов в правой полуплоскости комплексной плоскости s .
При ω → 0 АФХ разомкнутой системы стремится к бесконечности, а ее график претерпевает разрыв, т.е. не образует замкнутый контур.
График АФХ астатической системы с двумя интегрирующими звеньями (ν = 2) показан на рис.4.25.
122

Im
0 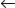 ω
ω
(−1; j0) |
0 |
Re |
|
|
ω |
Рис.4.25. График АФХ астатической системы второго порядка, имеющий разрыв при ω → 0
Для астатических систем трудно решить вопрос об устойчивости замкнутой
системы, так как неясно, охватывает график ее АФХ критическую точку (−1; j0) или нет. Соответствующие доказательства показывают, что критерий устойчивости
Найквиста для замкнутых астатических систем по отношению к ранее рассмотренным статическим системам не изменяется, но вносятся специфические изменения в вид АФХ.
Во-первых, будем, как и ранее, полагать s = jω , если ω изменяется в пределах 0 < ω < ∞ . Во-вторых, при ω → 0 положим s = ρexp( jϕ) , причем ρ → 0 , а ϕ изменяется в
пределах 0 ≤ ϕ ≤ π / 2 . Геометрически это означает, что на комплексной плоскости
начало координат, в котором аргумент argW ( jω) не имеет определенного значения, обходится по дуге бесконечно малого радиуса (рис.4.26).
|
|
|
Im |
|
|
|
|
s = jω |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
s = ρexp(jω) |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
ϕ = π/2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
0 |
|
|
|
ϕ = 0 |
|
Re |
|
|
|||||||
|
|
|
|
|
|
|
|||||||||||
|
Рис.4.26. Устранение неопределенности |
||||||||||||||||
|
аргумента в точке начала координат |
|
|||||||||||||||
При изменении s вдоль дуги бесконечно малого радиуса ρ , с учетом того, что |
|||||||||||||||||
s = ρexp( jϕ) ; |
|
|
|
|
|
|
|
|
R(s) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
= k, |
|
|
|
|
|
|
||||
|
|
|
|
|
|
Q(s) |
|
|
|
|
|
|
|||||
получим: |
|
|
|
|
|
s→0 |
|
|
|
|
|
|
|
|
|||
|
|
R(s) |
|
|
|
|
|
R(s) |
|
|
k |
|
|
|
k |
|
|
limW (s) = lim |
|
≈ |
|
|
|
|
= |
|
|
= |
e− jϕγ. |
||||||
(s)γ Q(s) |
|
|
|
|
|
ργe jϕγ |
ργ |
||||||||||
s→0 |
s→0 |
|
|
(ρe jϕ )γ Q(s) |
|
(4.32) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из соотношения (4.32) можно сделать следующий вывод: если точка s на комплексной плоскости корней обходит в положительном направлении (против часовой стрелки) дугу бесконечно малого радиуса, то соответствующая ей точка на
плоскости W (s) двигается в отрицательном направлении по дуге бесконечно большого
радиуса
123
lim |
k |
e− jϕγ = ∞ |
|||
|
|||||
ρ→0 |
ργ |
, |
|||
при этом 0 ≤ ϕ ≤ π / 2 и приращению аргумента |
arg(s) = π / 2 соответствует |
||||
приращение аргумента argW (s) , вычисляемое по формуле |
|||||
argW (s) = −γϕ , |
|||||
т.е. равное |
|
|
π |
|
|
argW (s) = − |
γ |
||||
|
|||||
|
2 . |
||||
С помощью такого приема удается устранить исходную неопределенность
аргумента argW (s) при s = 0 . Напомним, что нуль является комплексным числом, не имеющим определенного значения аргумента.
Следовательно, чтобы судить об устойчивости САУ, имеющей интегрирующие звенья, необходимо график АФХ разомкнутой системы дополнить следующим
построением. Точку АФХ, уходящую в бесконечность при ω → 0 , соединить с положительной полуосью действительной оси дугой. Эта дуга проводится радиусом бесконечно большого модуля из начала координат по часовой стрелке (в
− π γ
отрицательном направлении). Поворот вектора составляет угол 2 . После указанного
построения критерий устойчивости Найквиста к астатическим системам применяется обычным способом.
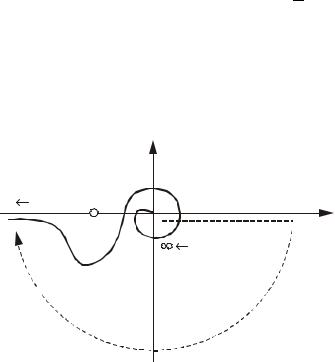
Пример использования полученного подхода иллюстрирует рис.4.27 применительно к астатической системе второго порядка. Данная система в замкнутом состоянии является устойчивой, так как график ее АФХ после проведенных
дополнений не охватывает критическую точку (−1; j0) . |
|
||
|
|
Im |
|
0 |
ω |
|
|
|
(−1; j0) |
0 |
Re |
|
|
ω |
|
Рис.4.27. График АФХ астатической системы второго |
|||
|
порядка после дополнительных построений |
|
|
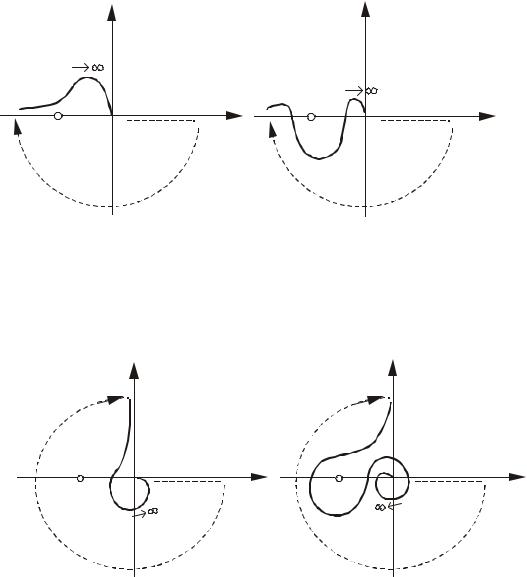
На рис.4.28 показаны графики АФХ еще двух систем с астатизмом второго |
|||
порядка. Левый график относится к неустойчивой системе, критическая точка попадает |
|||
в замкнутый контур, правый график - к устойчивой, критическая точка находится вне |
|||
замкнутого контура. |
|
|
|
124
|
|
Im |
|
|
ω |
|
|
− |
1; j0) |
0 |
Re |
( |
|
||
|
|
а |
|
Im |
|
|
ω |
|
|
(−1; j0) |
0 |
Re |
|
б |
|
Рис.4.28. Графики АЧХ астатических систем второго порядка после дополнительных построений: a - неустойчивой в замкнутом состоянии; б -
устойчивой замкнутом состоянии
Соответствующие примеры систем третьего порядка приведены на рис.4.29.
|
Im |
|
|
Im |
|
|
(−1; j0) |
0 |
Re |
(−1; j0) |
0 |
ω |
Re |
|
ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
б |
|
|
Рис.4.29. Графики АФХ астатических систем третьего порядка после дополнительных построений: a - неустойчивой в замкнутом состоянии; б -
устойчивой замкнутом состоянии
При определении устойчивости замкнутой системы, неустойчивой в разомкнутом состоянии и содержащей интегрирующие звенья, критерий устойчивости Найквиста после дополнительных построений применяется обычным способом.
Для устойчивости замкнутой системы необходимо и достаточно, чтобы график
АФХ разомкнутой системы после проведенных дополнений охватывал в
положительном направлении точку (−1; 0) l / 2 раз, где l - число корней ее характеристического уравнения, лежащих в правой полуплоскости комплексной плоскости.
4.7. Логарифмический критерий устойчивости
Для определения устойчивости САУ по критерию Найквиста можно строить ЛЧХ, а не АФХ, что значительно упрощает применение критерия. Кроме того,
построенные ЛЧХ могут быть использованы в дальнейшем при исследовании качества САУ и синтезе корректирующих устройств. При использовании ЛЧХ об устойчивости
125
замкнутой САУ судят по совместному поведению ЛАЧХ и ЛФЧХ разомкнутой системы.
Ранее было показано, что устойчивость замкнутой системы связана с числом переходов АФХ разомкнутой системы через отрезок (−∞; −1). Рассмотрим, как,
используя ЛЧХ разомкнутой системы, определить число пересечений отрезка (−∞; −1) АФХ разомкнутой системы.
В том случае, когда АФХ пересекает отрицательную вещественную ось, ЛФЧХ пересекает одну из линий: ±π ; ±3π ; ±5π , … . Так как фазовая характеристика системы определяется с точностью до периода 2π , то чтобы сделать ее однозначной, условимся рассматривать значения фазы в интервале (–2π; 0).
Тогда пересечению АФХ разомкнутой системы отрезка сверху вниз (положительный переход) будет соответствовать пересечение уровня −π снизу вверх при положительной логарифмической амплитудной характеристике. Следовательно, пересечение ЛФЧХ уровня −π снизу вверх при положительной ЛАЧХ следует считать за положительный переход, а пересечение уровня −π сверху вниз при положительной ЛАЧХ - за отрицательный. Соответствие между переходами уровня −π на АФХ и ЛФЧХ поясняется рис.4.30 и 4.31, где стрелками обозначены направления переходов и их знаки.
|
|
|
|
|
Im |
|
|
|
|
|
p = 2 |
|
|
- |
|
|
ω |
|
|
3 |
2 |
|
|
+ |
|
+ |
|
||
|
|
|
|
||
6 |
5 |
4 |
(−1; j0) |
8 |
Re |
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
1 |
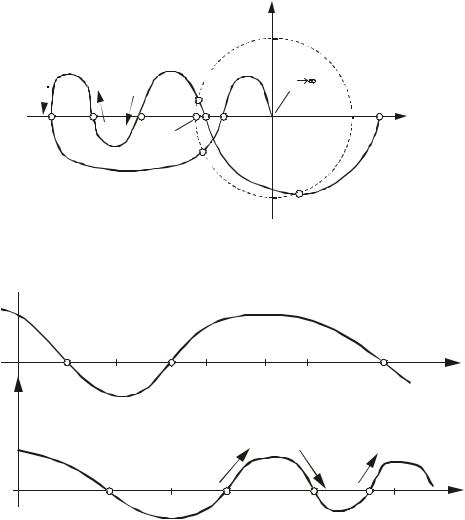
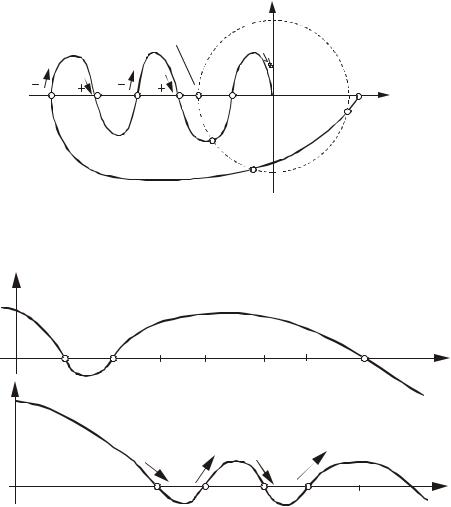
Рис.4.30. График АФХ неустойчивой разомкнутой |
|||||
системы (p = 2), устойчивой в замкнутом состоянии |
|||||
Lm(ω) 
|
|
|
|
|
|
|
|
lg ω |
1 |
2 |
3 |
4 |
5 |
6 |
|
7 |
ω |
ϕ(ω) |
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
+ |
|
lg ω |
−π |
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
ω |
||
|
2 |
3 |
|
4 |
5 |
6 |
7 |
Рис.4.31. Графики ЛЧХ неустойчивой разомкнутой системы (p = 2),
устойчивой в замкнутом состоянии
126
Формулировка логарифмического критерия. Для того чтобы система,
неустойчивая в разомкнутом состоянии и имеющая p полюсов в правой полуплоскости комплексной плоскости s , была устойчива в замкнутом состоянии, необходимо и достаточно, чтобы на тех частотах, где ЛАЧХ положительна, ЛФЧХ пересекала
n+ − n− = |
p |
|
|
2 , где n+ и n− - соответственно количество |
|||
уровень −π так, чтобы |
|||
положительных и отрицательных переходов.
Пример. Определить устойчивость замкнутой системы, которая в разомкнутом состоянии неустойчива (количество правых корней p = 2). АФХ системы приведена на рис.4.30. Из рассмотрения АФХ видно, что она один раз охватывает критическую точку в положительном направлении. Следовательно, замкнутая система устойчивая. Тот же
вывод относительно устойчивости замкнутой системы можно получить гораздо проще на основании ЛЧХ (см. рис.4.31) по логарифмическому критерию, подсчитав количество положительных (два) и отрицательных (один) переходов и найдя их разность (один).
Аналогичные соображения справедливы и для замкнутой системы, устойчивой в разомкнутом состоянии. Например, рассмотрим АФХ и ЛЧХ системы, показанные соответственно на рис.4.32 и 4.33.
|
|
|
|
Im |
|
|
|
|
(−1; j0) |
|
|
|
|
|
|
ω |
|
|
|
|
|
|
ω = 0 |
3 |
4 |
5 |
6 |
8 |
Re |
|
|
|
|
|
1 |
|
|
|
|
7 |
|
|
|
|
|
2 |
|
|
Рис.4.32. График АФХ устойчивой разомкнутой |
||||
|
системы, имеющей по два положительных и |
|
|||
|
|
|
отрицательных перехода |
|
|
Lm(ω) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lg ω |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
ω |
ϕ(ω) |
|
|
|
|
|
|
|
|
|
+ |
|
+ |
|
lg ω |
|
−π |
|
− |
|
− |
|
|
|
3 |
4 |
5 |
6 |
7 |
ω |
||
|
Рис.4.33. Графики ЛЧХ устойчивой разомкнутой системы,
имеющей по два положительных и отрицательных перехода
127
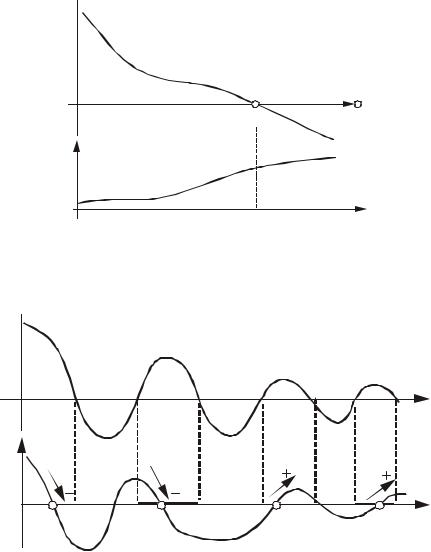
Количество положительных и отрицательных переходов одинаковое, равное двум, следовательно, замкнутая система устойчивая, однако ЛЧХ анализировать проще.
Из формулировки логарифмического критерия можно сделать следующий важный вывод: для того чтобы система, устойчивая в разомкнутом состоянии, была устойчива в замкнутом состоянии, необходимо и достаточно, чтобы на частотах, где
ЛАЧХ положительна ( L m (ω) > 0 ), фазовая частотная характеристика:
∙либо не пересекала линию, соответствующую значению фазы ϕ = −π
(рис.4.34);
∙ либо пересекала линию ϕ = −π четное число раз, т.е. чтобы n+ = n− (рис.4.35).
Lm(ω)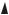
lg ω
ωc |
ω |
ϕ(ω) |
|
−π |
lgω |
|
ω |
Рис.4.34. Графики ЛЧХ разомкнутой системы, устойчивой в разомкнутом состоянии. На частотах, где ЛАЧХ положительна, ЛФЧХ не пересекает линию –π
Lm(ω)
lg ω
ω
ϕ(ω) |
|
|
|
|
−π |
|
|
|
lg ω |
1 |
2 |
3 |
4 |
ω |
Рис.4.35. Графики ЛЧХ разомкнутой системы, устойчивой в разомкнутом состоянии. На частотах, где ЛАЧХ положительна, ЛФЧХ пересекает линию –π по два раза в отрицательном и положительном направлениях
Аналогично исследованию устойчивости статических систем устанавливается устойчивость астатических систем. Однако следует помнить об особенностях дополнительного построения на графике АФХ. На рис.4.36 показана АФХ астатической системы, дополненная дугой бесконечно большого радиуса. Эта система является устойчивой в замкнутом состоянии, так как АФХ разомкнутой системы не охватывает критическую точку.
128
