
- •Раздел 1. Пространство элементарных событий (пэс). Операции над случайными событиями
- •Раздел 2. Классическое определение вероятности
- •Раздел 3. Условная вероятность. Независимость событий
- •Раздел 4. Теоремы сложения и умножения вероятностей
- •Раздел 5. Формула полной вероятности. Формула Байеса
- •Раздел 6. Испытания Бернулли
- •Раздел 7. Теорема Муавра-Лапласа и Пуассона
- •Раздел 8. Функция распределения и числовые характеристики случайной величины
- •Раздел 9. Основные типы распределений случайных величин
- •Раздел 10. Двумерные случайные величины. Зависимость случайных величин
- •Раздел 11. Предварительная обработка выборки. Эмпирическая функция рапределения. Точечные оценки числовых характеристик генеральной совокупности.
- •Раздел 12. Доверительный интервал
- •Раздел 13. Проверка статистических гипотез
- •Раздел 1
- •Раздел 5
- •Раздел 9
- •Раздел 10.
- •Раздел 11.
- •Раздел 12.
- •Раздел 13.
Раздел 1
а) {ГГГ, ГГР, ГРГ, РГГ, РРГ, РГР, ГРР, РРР},
б) A= {ГРР, РГР, РРГ},B={ГГР, ГРГ, РГГ},C={ГГР, ГРГ, РГГ, ГГГ},
в) 3/8, 3/8, 1/2
2.
![]()
3. а)
нет, б)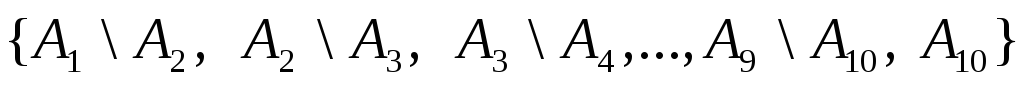 ,
,
в)
![]()
Раздел 2
1. 3/10, 7/10
2. а) 1/3 , б) 1\2 , в) 0
3. а) 1/6 , б) 1/3 , в) 1/ 2, г) 1/3
4.а) 1/36, б) 1/18, в) 5/18, г) 11/36
5. ![]()
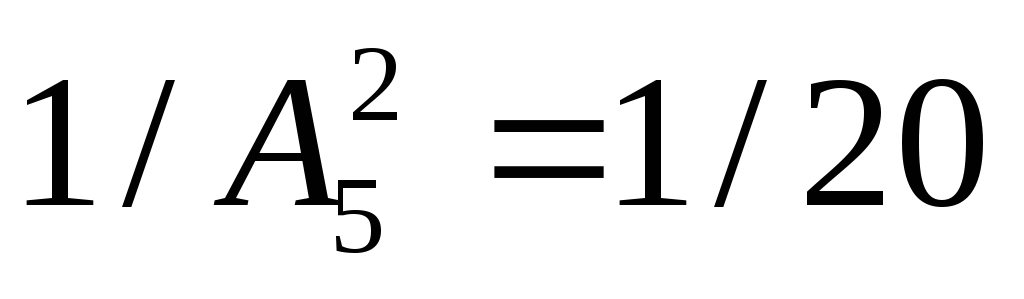
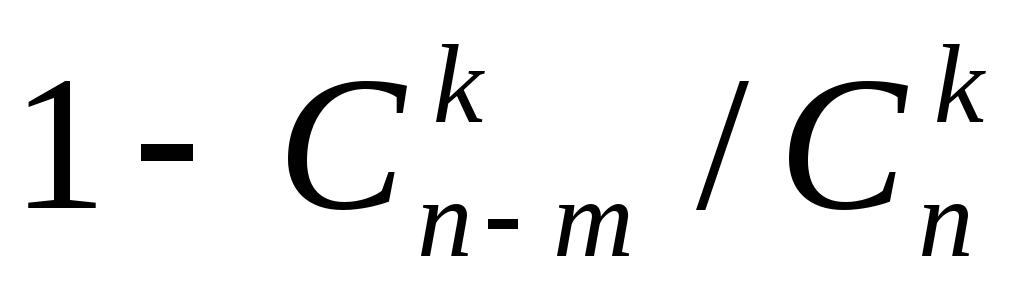


(m – 1) / (n – 1)
(m – 1) / (n – 1)
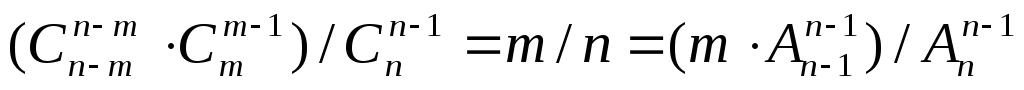

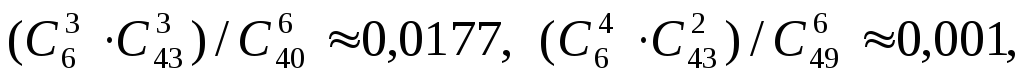
![]()
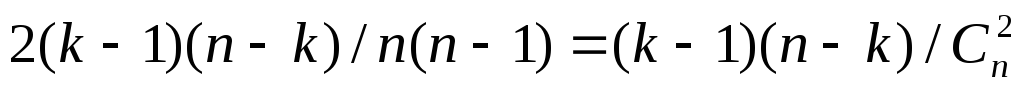
¼
Раздел 3
2/3
2/9 , 1/3
Зависимы:
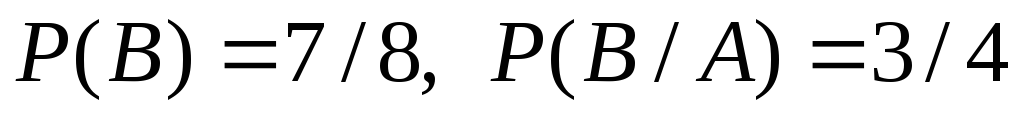
Зависимы:
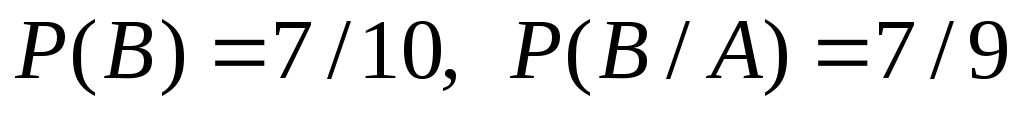
2/3
Нет:
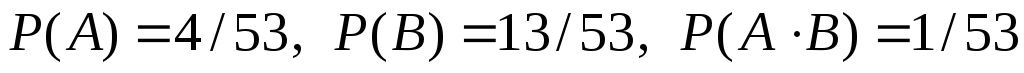 ,
так что
,
так что
![]()
=
![]() поэтому событияA,B,Cпопарно независимы. Но
поэтому событияA,B,Cпопарно независимы. Но![]() ,
так что события
,
так что события
A,B,C зависимы в совокупности.
Раздел 4
1. а) 0,98 , б) 0,26 , в) 0,02
2. 1/126
3.
1/216 , 1/36 ,
![]()
5/8
5. 7/9
6. 1/2
28/29 . Замечание: задачу проще решить переходом к противоположному событию.
65/81
0,1. Найти аналогию с «хорошим» билетом на экзамене. 0,5
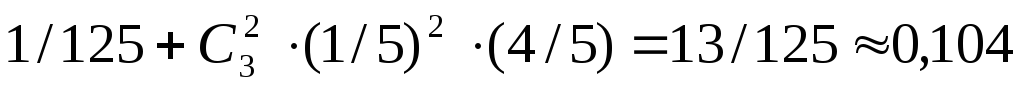
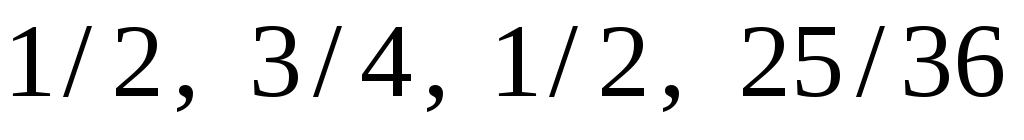 ,
,
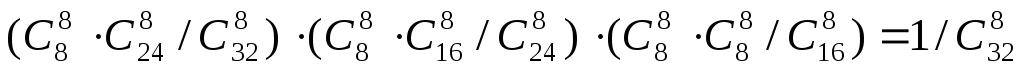
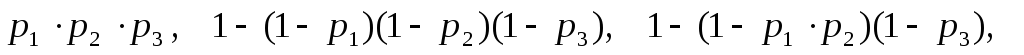
![]()
В системе 1 :
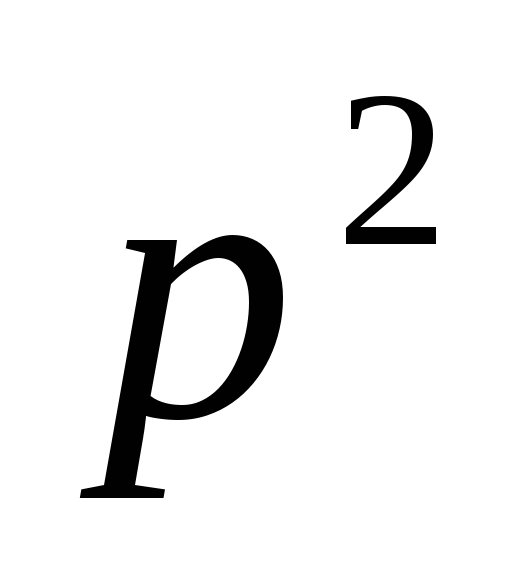 - вероятность работы верхней цепи (из
элементов 1, 2) и
- вероятность работы верхней цепи (из
элементов 1, 2) и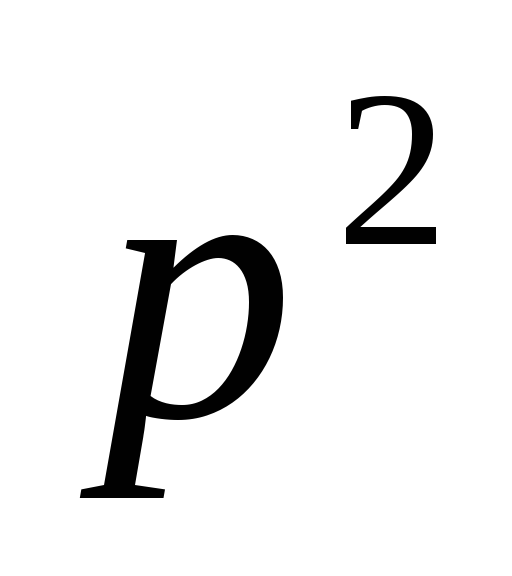 - вероятность работы нижней цепи (из
элементов 3, 4). Поэтому вероятность
работы системы 1 равна
- вероятность работы нижней цепи (из
элементов 3, 4). Поэтому вероятность
работы системы 1 равна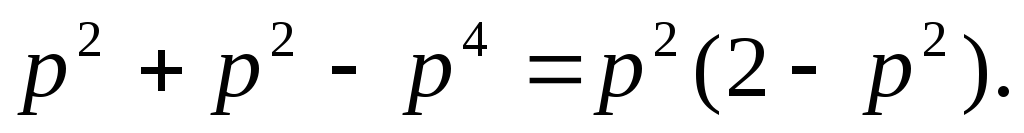
В
системе 2:
![]() - вероятность работы левого звена (из
элементов 1, 3) и
- вероятность работы левого звена (из
элементов 1, 3) и![]() - вероятность работы правого звена (из
элементов 2, 4). Поэтому вероятность
работы системы 2 равна
- вероятность работы правого звена (из
элементов 2, 4). Поэтому вероятность
работы системы 2 равна![]()
![]() Следовательно, вторая система надёжнее.
Следовательно, вторая система надёжнее.
16. Событие А – жюри примет правильное решение – является суммой следующих несовместных событий: (1-ый судья – правильное решение, и 2-ой судья - правильное решение, и 3-ий судья – правильное решение) + (1-ый судья – правильное решение, и 2-ой судья - правильное решение, и 3-ий судья – неправильное решение) + (1-ый судья – неправильное решение, и 2-ой судья - правильное решение, и 3-ий судья – правильное решение) + (1-ый судья – правильное решение, и 2-ой судья - неправильное решение, и 3-ий судья – правильное решение) . Каждое слагаемое в сумме – произведение независимых в совокупности событий. Поэтому:
![]()
Вероятность принятия жюри правильного решения равна
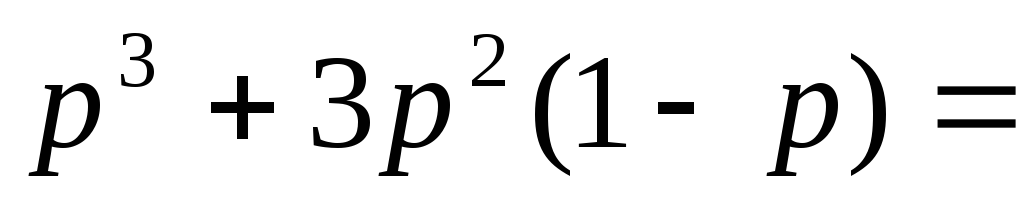
![]() Неравенство
Неравенство![]() выполнено при
выполнено при![]()
Вероятность принятия жюри правильного решения равна
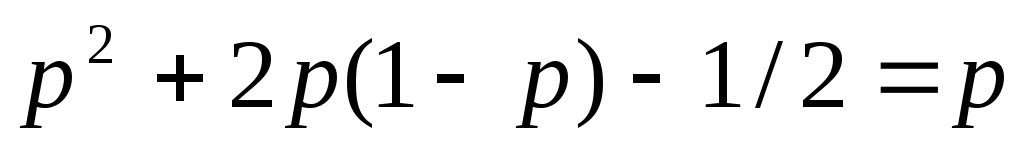
609/625
Раздел 5
13/30
11/20 , 4/5 , 11/100
1
m/n
67/120
0,52. Короткое решение. Событие А - вынут белый шар. Гипотезы:
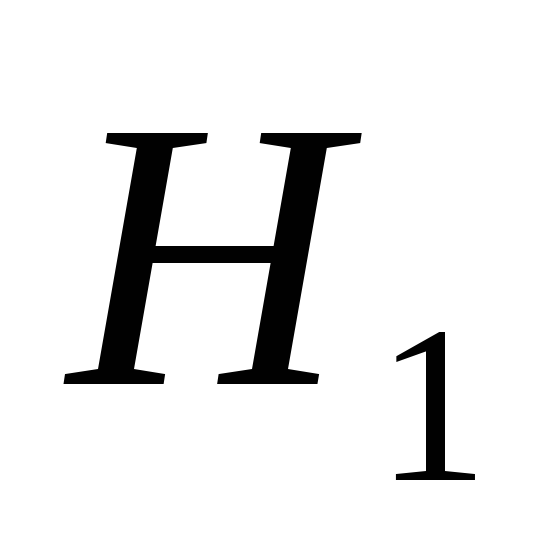 - вынутый из второй урны шар принадлежал
первой урне;
- вынутый из второй урны шар принадлежал
первой урне;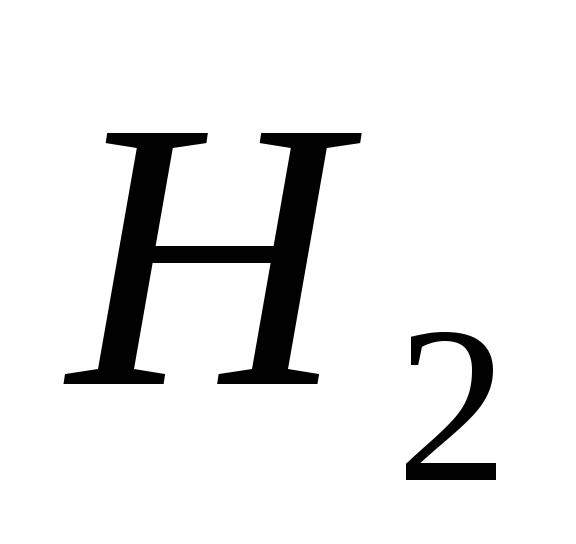 - вынутый из второй урны шар принадлежал
второй урне.
- вынутый из второй урны шар принадлежал
второй урне.
![]()

0,78
0,816
10
11. 20/21
6/7 . Указание: полная сумма событий в данном опыте состоит из четырёх гипотез.
2/3 , 1/2, 1/3
0,41
0,77 , 0,19 , 0,04
0,64 , 0,16 , 0,04
Раздел 6
1. 5/16 , 13/16 , 1/32
27/128
Выиграть 2 встречи из четырёх. Как объяснить это, используя числовые характеристики биномиального распределения?
0,77, 0,02
0,373
0,737
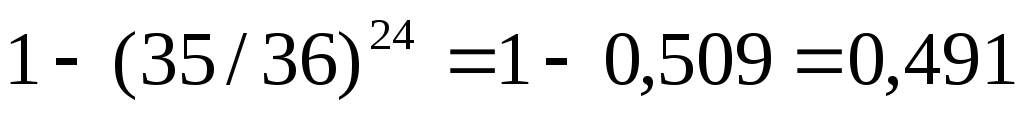
Вероятность того, что при nбросаниях «шестёрка» не выпадет ни разу равна
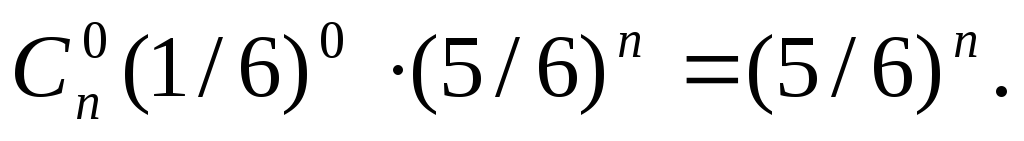 Решая неравенства
Решая неравенства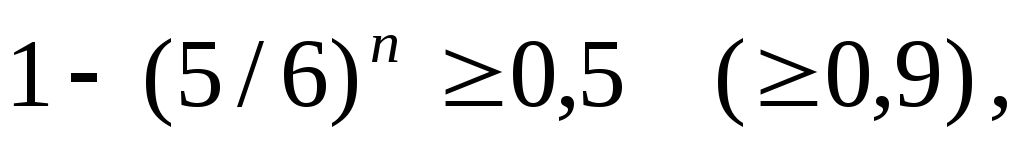 получим:
получим:
а) n ≥ 4 , б)n ≥ 13
0,019
Раздел 7
1. 0,0798 , 0,011 , ≈ 0
2. 0,0532, 0,022
3.0,052
4.0,682
0,97
0,972
От 4 до 23. Применить правило «трёх сигм».
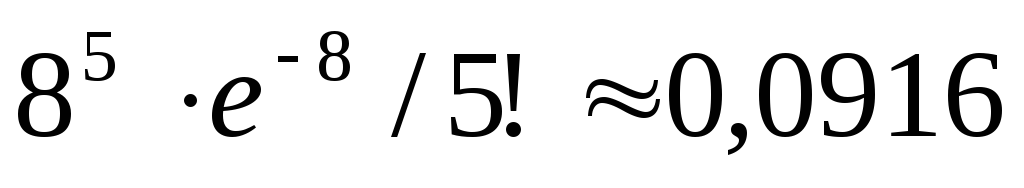
0,2385

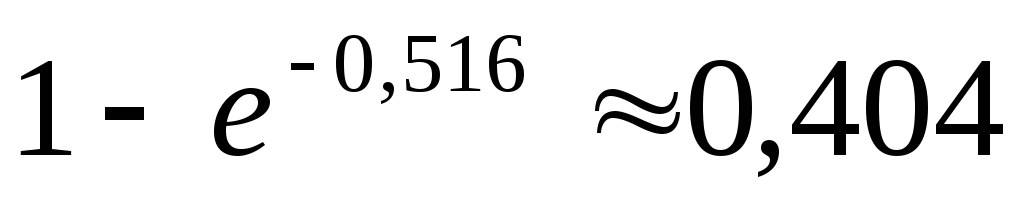
0,1755 , 0, 0181 , 0,0067 , 0,9933
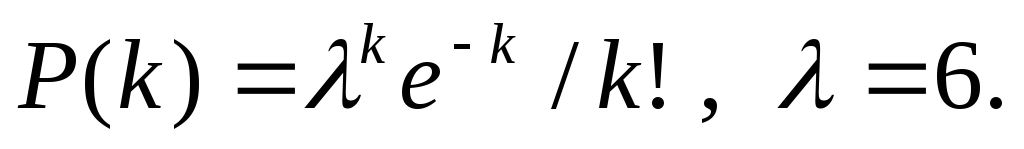
а) неравенство для нахождения k: 120000 ≤ 1000۰ k,
![]()
б) неравенство для нахождения k: 80000 ≥ 1000۰ k,
![]()
Раздел 8
б)
 ,
,
в) 0,8 , г) 0,2 , 1,36 , 1,17 , 5,85 , любая точка в интервале [1, 0], 1
д)
![]()
2. б)
 , в) 1, г) 1/6 , 5/36 ,
, в) 1, г) 1/6 , 5/36 ,
![]() ,
,
![]() ,
0 , 0, д)
,
0 , 0, д)![]()
3. б)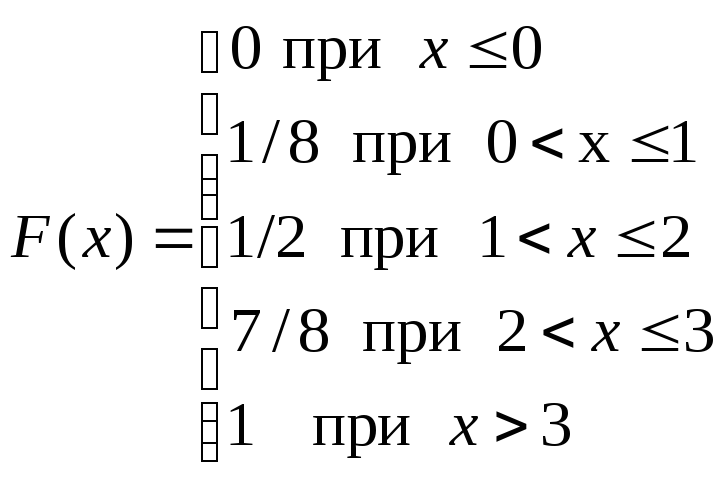 ,
,
в) 1/2,
г) 3/2 , 3/4,
![]() ,
любая точка интервала [1, 2], два значения:
1 и 2,
,
любая точка интервала [1, 2], два значения:
1 и 2,
д)
![]()
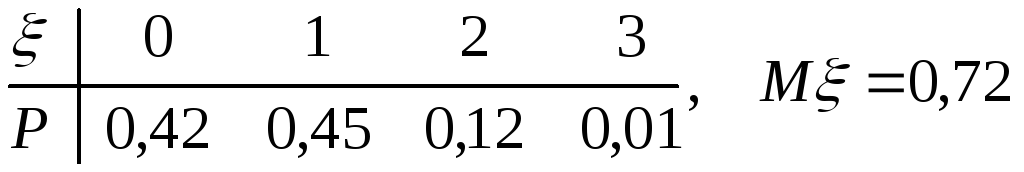
а)
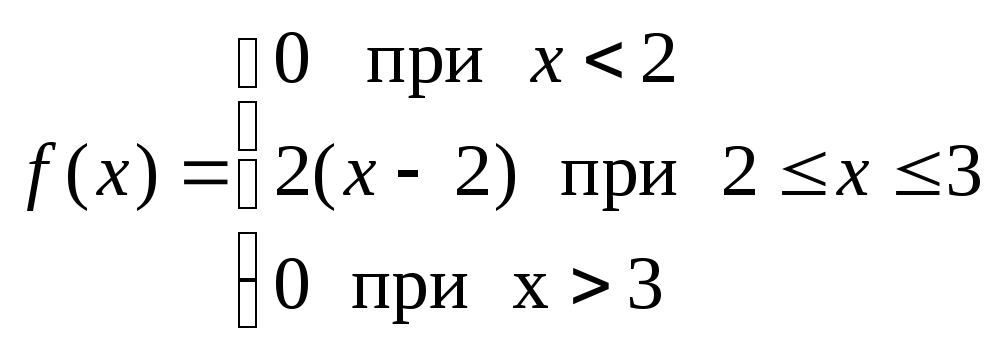 , б) 0,25 , в) 0,75
, б) 0,25 , в) 0,75а)
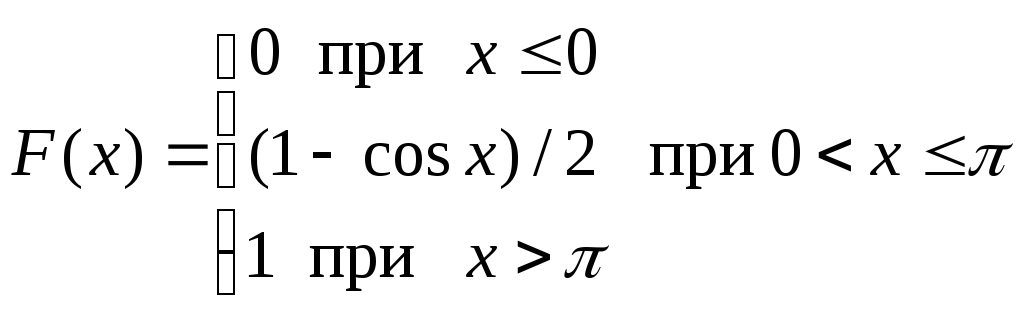 , б)
, б)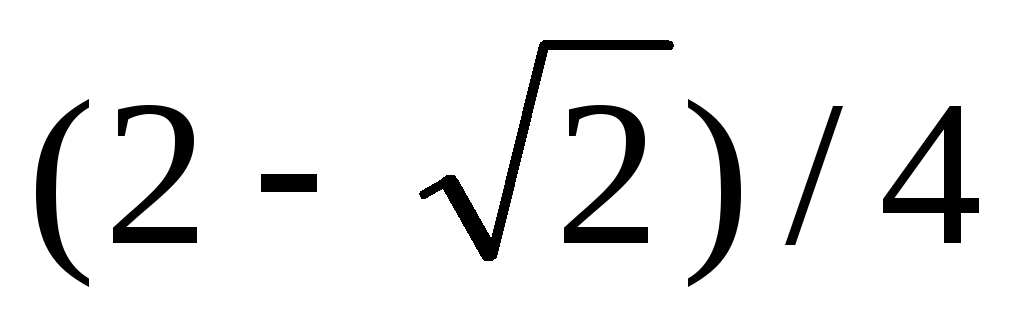
–3 , 160 ,
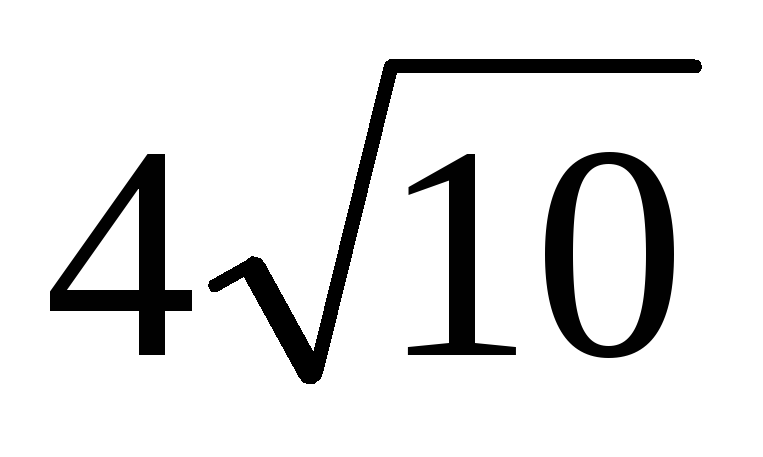
а) 7/2 , 35/12 , ≈ 1,71 ; б)
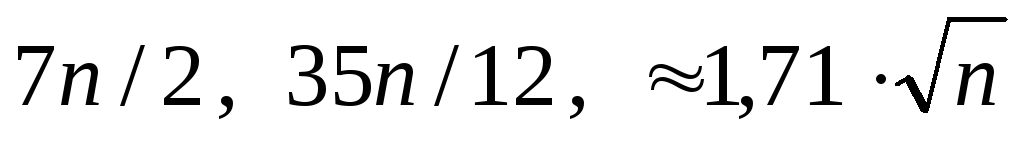
Пусть центр круга радиуса Rрасположен в начале координат. Если (x,y) – координаты брошенной в круг точки, то
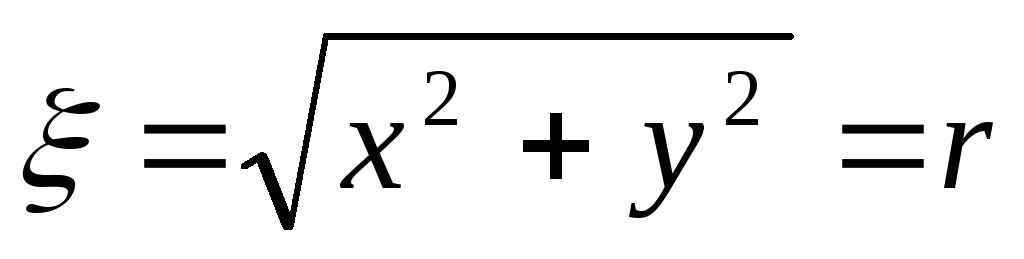 - длина радиус-вектора точки. При
- длина радиус-вектора точки. При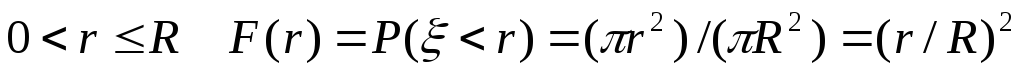 .
Поэтому
.
Поэтому
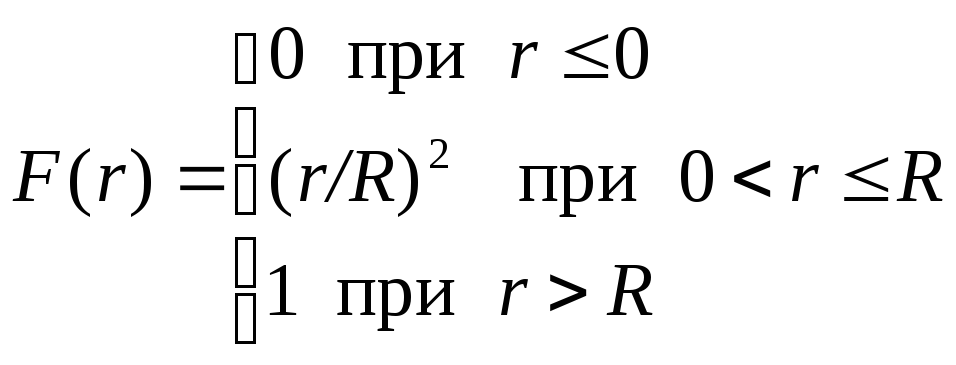
Плотность
распределения ξ равна
![]()
![]()
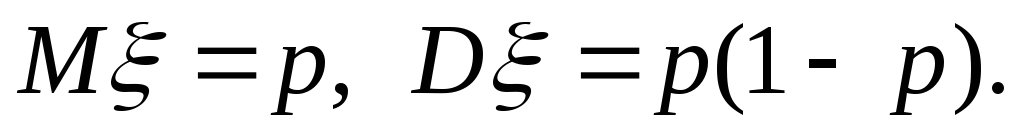 Квадратичное неравенство
Квадратичное неравенство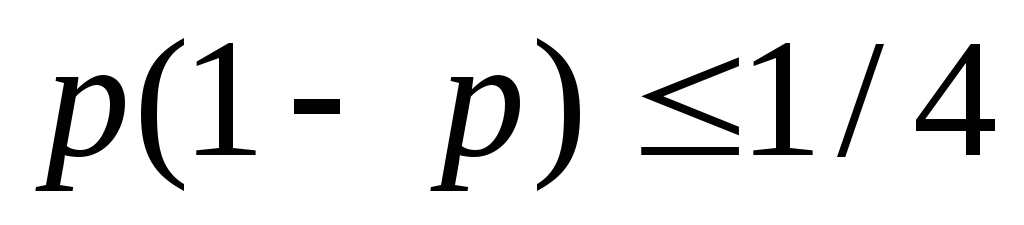 выполняется при любом значенииp.
выполняется при любом значенииp.
