2. Фильтрация сигналов на фоне помех

2.1. Постановка задачи фильтрации

Пусть на входе системы действует колебание

x(t) = F [s(t,l), n(t)],

где s(t,l) – полезный сигнал, n(t) – помеха, l – совокупность интересующих нас параметров l_i(t), причем сам сигнал s(t,l), или параметр l_i(t) – случайные процессы. Помеха n(t) может быть произвольной; сигнал и помеха не обязательно представляют собой аддитивную смесь. Считается, однако, что вид функции F (т. е. способ комбинирования сигнала и помехи) и некоторые статистические характеристики случайного сигнала и помехи нам известны. С учетом этих априорных сведений нужно решить, какая из возможных реализаций самого сигнала s(t, l) или его параметра l содержится в принятом колебании x(t). Из-за наличия помех и вследствие случайного характера сигнала оценка реализации сигнала или его параметра зачастую не будет совпадать с истинным значением, что приводит к ошибкам фильтрации. К тому же к фильтрам, предназначенным для использования в различных устройствах, предъявляются различные, порой противоречивые требования. Поэтому и характеристики фильтров должны удовлетворять различным критериям. Фильтры, предназначенные для устройств обнаружения, должны обеспечить максимум отношения сигнал/помеха. Фильтры, предназначенные для устройств измерения тех или иных параметров, должны отвечать критерию минимума среднеквадратической погрешности. Возможны и другие виды критериев, по которым строятся характеристики.

2.2. Оптимальные фильтры устройств обнаружения

Оптимальные линейные фильтры широко применяются при обнаружении и различении детерминированных сигналов, причем критерием оптимальности характеристик таких фильтров является получение на выходе фильтра максимально возможного отношения пикового значения сигнала к среднеквадратическому значению помехи. Цель обработки при этом состоит не в воспроизведении формы сигнала, которая считается известной, а в наиболее надежной фиксации лишь факта наличия или отсутствия сигнала в принятом колебании.

Найдем выражение для комплексной частотной характеристики оптимального фильтра [5]. Пусть на вход линейного фильтра с комплексной частотной характеристикой K(j) воздействует сумма полностью известного сигнала s(t) и помехи n(t), представляющей собой стационарный в широком смысле случайный процесс с известной спектральной плотностью S_n() [4]:

x(t) = s(t) + n(t) , 0 £ t £ T .

Обозначим полезный сигнал и помеху на выходе фильтра через s_в(t) и n_в(t). Известно, что если на вход линейной системы с комплексной частотной характеристикой K(j) воздействует сигнал s(t), имеющий комплексный амплитудный спектр

,

то комплексный спектр сигнала на выходе системы определяется произведением Ф(j)K(j), а сам выходной сигнал – выражением

. (2.1)

Спектральная плотность помехи на выходе фильтра определяется выражением S_n(w)|K(jw)|², а ее дисперсия

. (2.2)

На основании формул (2.1) и (2.2) получаем выражение для отношения сигнал / помеха по мощности на выходе фильтра в некоторый момент времени t₀ :

. (2.3)

Необходимо найти такую функцию K(jw), при которой выражение (2.3) в некоторый момент времени t₀ достигает максимума. Одним из путей решения этой задачи является использование неравенства Шварца-Буняковского. Известно, что для двух произвольных комплексных функций f(x) и g(x) выполняется соотношение

, (2.4)

причем знак равенства имеет место только в случае, когда g(x) = c₀ f(x), где c₀ – постоянная; f*(x) – функция, комплексно-сопряженная f(x).

Запишем выражение (2.4), перейдя к переменной , в виде

.

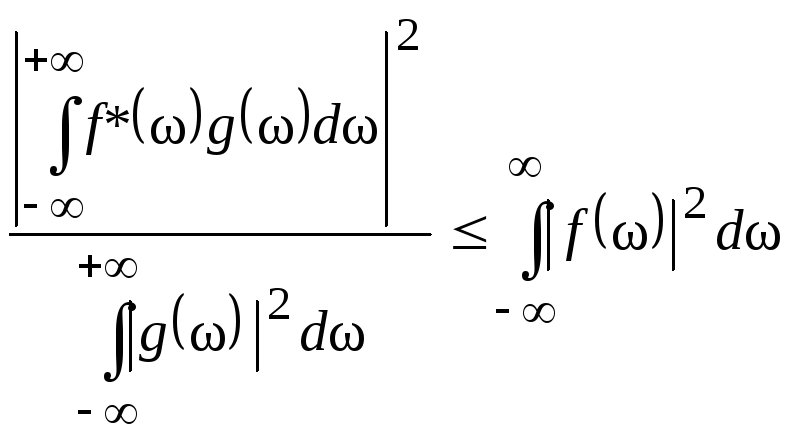Полагая здесь

(2.5)

получаем

(2.6)

Отсюда следует, что максимально возможное значение отношения сигнал / помеха

(2.7)

Согласно соотношению (2.5), это значение достигается лишь при выполнении условия

,

или

(2.8)

где c – некоторая постоянная; t₀ – момент времени, соответствующий наибольшему значению отношения сигнал/помеха на выходе фильтра. Таким образом, комплексная частотная характеристика оптимального линейного фильтра определяется формулой (2.8), а наибольшее отношение сигнал помеха – выражением (2.7). Варьируя спектры сигнала Ф(jw) и помехи S_n(w) в формуле (2.7), можно при некоторых дополнительных условиях (например, постоянство энергии или мощности сигнала и др.), налагаемых на систему, найти наилучшую форму спектра сигнала (при которой максимизируется Q ) и наихудшую спектральную плотность помехи (при которой Q минимизируется).

В некоторых устройствах, например служащих для определения момента появления импульса, применяются фильтры, которые должны обеспечивать получение максимально возможного отношения крутизны сигнала к среднеквадратическому значению помехи. Такие фильтры можно назвать оптимальными по крутизне сигнала. Для определения комплексной частотной характеристики такого фильтра вместо самого сигнала s(t) надо рассматривать его производную по времени . При этом комплексная частотная характеристика фильтра, оптимального по крутизне сигнала, определяется выражением

,

где Ф₁^*(j) – комплексно-сопряженное значение спектра производной входного сигнала; с₁ – некоторая постоянная. Максимально возможное отношение крутизны сигнала к среднеквадратическому значению помехи будет

.

Используя известное соотношение для преобразования Фурье производной сигнала:

,

можно записать:

.

Тогда

,

.