1.3. Статистические характеристики реверберации

Для определения статистических характеристик необходимо располагать сведениями о законах распределения случайных параметров N(t), _i , t_i . Если предполагать, что рассеиватели в среде расположены независимо и с точки зрения рассеивающих свойств не влияют друг на друга, то эти параметры следует считать статистически независимыми. Кроме того, обычно можно считать, что вероятностные законы распределения случайных параметров не зависят от номера i . Все это позволяет проводить статистическое усреднение по параметрам N, _i , t_i раздельно.

Пусть p(N, t) – закон распределения числа N(t) элементарных сигналов. Тогда среднее значение комплексной огибающей реверберации

, (1.1)

причем индексы i при проведении усреднения в (1.1) опущены, так как считается, что вероятностные характеристики элементарных сигналов от номера не зависят. Введем n(t) – среднее число элементарных сигналов, приходящих в точку приема в единицу времени. Тогда среднее число элементарных рассеянных сигналов, создающих реверберацию в момент времени t:

, (1.2)

где T_эф – эффективная длительность излучаемого сигнала. Будем в дальнейшем считать, что t_i = t’, а также что функция M(t’) незначительно меняется в пределах интервала [t–T_эф /2; t+T_эф /2 ]. Тогда M(t’) = M(t) и

, (1.3)

где – среднее значение случайных величин_i . Подставляя (1.3) и (1.2) в (1.1), получим

. (1.4)

Усреднение в (1.4) ведется по в пределах эффективной длительности импульсаT_эф . Учитывая, что плотность распределения вероятностей величины может быть записана как,T_эф много больше периода несущей частоты (T_эф >> 2/₀₎ , результат усреднения дает 0 (среднее от гармонического процесса на протяжении нескольких периодов). Следовательно, m_p(t)@ 0 .

Следует отметить, что этот вывод сделан для комплексной огибающей, а не для вещественной.

Рассмотрим теперь комплексную огибающую сигнала реверберации в два момента времени: t и (t – ).

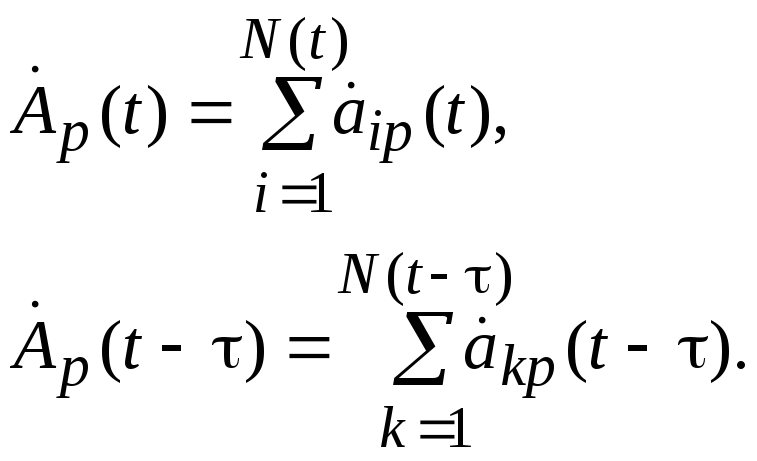
По определению, t – текущая корреляционная функция R_p(t, ) [4] комплексной огибающей:

Выделим в двойной сумме два слагаемых: первое для случая i = k и второе для i  k. Тогда

.

Второе слагаемое равно нулю в силу независимости рассеяния на отдельных рассеивателях. Тогда, вводя, как и при вычислении среднего значения, распределение p(N, t), можно записать:

.

Учитывая статистическую независимость _k =  и , аналогично предыдущему можем записать

. (1.5)

Считая, как и раньше, закон распределения равномерным в интервале [t-T_эф /2; t+T_эф /2 ], , перепишем (1.5) в виде

Сделаем замену переменных и, пренебрегая “краевыми эффектами” излучаемого сигнала как временной функции, распространим пределы интегрирования на область [-¥ ; ¥] . Тогда окончательное выражение для корреляционной функции комплексной огибающей

(1.6)

Найдем дисперсию комплексной огибающей

, (1.7)

где – энергия сигнала.

Нормированная корреляционная функция комплексной огибающей из (1.7) и (1.6) определится как

. (1.8)

Из (1.7) видно, что дисперсия комплексной огибающей реверберации зависит от времени, т. е. реверберация является нестационарным процессом. Однако из (1.8) видно, что нормированная корреляционная функция от времени не зависит, т. е. реверберация относится к классу процессов, приводимых к стационарным.

Выражение (1.6) для корреляционной функции позволяет получить t-текущую спектральную плотность комплексной огибающей реверберации:

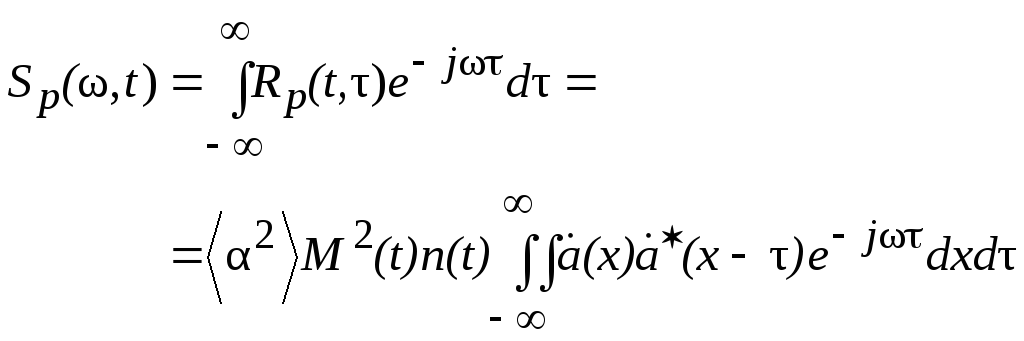
Вводя замену y = x– t , получим

где – амплитудный спектр комплексной огибающей зондирующего сигнала. Таким образом, видно, что спектральная плотность комплексной огибающей реверберации отличается от спектральной плотности комплексной огибающей зондирующего сигнала только зависящим от времени масштабным множителем. Следовательно, реверберация – это помеха, коррелированная с сигналом, что обусловливает значительные трудности обнаружения и измерения параметров сигнала на фоне реверберационной помехи.