Файловый архив студентов. Файловый архив студентов.
1261 вуз, 4614 предмет.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Воронежский государственный университет
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

Основы физической химии_Ерёмин

.pdf
Скачиваний:
992
Добавлен:
19.03.2016
Размер:
4.73 Mб
Скачать
☆

Г л а в а 4. Статистическая термодинамика

217

Диагональные элементы матрицы плотности равны вероятности того, что система находится в i-ом энергетическом состоянии и имеет энергию Ei:

 

 

 

Ei

ρi

= const exp

−

 

.

 

 

 

 

kT

Значение константы определяется условием нормировки (14.22):

const =

 

1

 

 

 

.

 

 

 

Ei

 

∑exp

−

 

 

 

 

i

 

 

kT

Знаменатель этого выражения называют суммой по состояниям (см. § 15). Он имеет ключевое значение для статистической оценки термодинамических свойств системы. Из (14.27) и (14.28) можно найти число частиц Ni, имеющих энергию Ei:

 

 

 

 

−

 

Ei

 

Ni

 

 

exp

 

 

 

 

 

 

 

 

 

 

 

=

 

 

 

 

kT

 

N

 

 

 

 

 

Ei

 

 

 

 

 

 

 

 

∑exp

−

 

 

 

 

kT

 

 

i

 

 

 

 

 

(14.27)

(14.28)

(14.29)

(N – общее число частиц). Распределение (14.29) частиц в каноническом ансамбле по уровням энергии называют распределением Больцмана (см. пример 14-1), а числитель этого распределения – больцмановским фактором (множителем). Иногда это распределение записывают в другом виде: если существует несколько уровней с одинаковой энергией Ei, то их объединяютводнугруппупутемсуммированиябольцмановских множителей:

 

 

 

 

 

 

Ei

 

Ni

 

gi exp

−

 

 

 

 

 

 

 

 

 

=

 

 

 

 

kT

 

N

∑gi

 

 

−

Ei

 

 

 

 

 

exp

 

 

 

 

kT

 

 

i

 

 

 

 

 

(gi – вырожденность энергетического состояния, то есть число уровней с одной и той же энергией Ei).

Многие макроскопические параметры системы, находящейся в тепловом равновесии с окружающей средой, можно вычислить с помощью распределения Больцмана. Например, средняя энергия определяется как среднее по уровням энергии с учетом их статистических весов:

 

 

 

∑Ei gi exp

 

−

Ei

 

 

 

Ni

 

 

 

 

 

 

 

 

 

kT

 

E = ∑Ei

=

i

 

 

 

 

 

.

N

∑gi

 

 

 

Ei

 

i

 

−

 

 

 

 

 

exp

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i

 

 

 

kT

 

 

(14.30)

(14.31)

218

Г л а в а 4. Статистическая термодинамика

ПРИМЕРЫ

Пример 14-1. Рассмотрим изолированную систему, состоящую из N одинаковых молекул в объеме V. Каждая молекула находится на одном из энергетических уровней Ei. При каком распределении молекул по уровням Ni термодинамическая вероятность будет максимальна (с учетом постоянства общей энергии E и числа частиц N)?

Решение. Пусть на i-м уровне находится Ni молекул. Термодинамическая вероятность такого распределения по уровням описывается уравнением (14.4):

W =

N !

 

.

N1 !N 2 !...N k !

Используя формулу Стирлинга lnx! ~ x lnx – x, найдем логарифм термодинамической вероятности:

lnW = N ln N − ∑k Ni ln Ni .

i=1

Максимум этой функции при дополнительных условиях

N = ∑k Ni ,

i=1

E = ∑k Ni Ei

i=1

находится методом неопределенных множителей Лагранжа. Функция ln W имеет максимум, а N и E – константы, поэтому их дифференциалы равны 0:

d lnW = −∑k (ln Ni + 1) dNi = 0 ,

i=1

dN = ∑k dNi = 0 ,

i=1

k

dE = ∑Ei dNi = 0 .

i=1

Для того, чтобы учесть условия постоянства энергии и числа частиц, умножим второе и третье уравнения на неопределенные множители α и β и вычтем первое уравнение:

∑k (ln Ni + 1 + α + βEi ) dNi = 0 .

i=1

Г л а в а 4. Статистическая термодинамика

219

Теперь дифференциалы dNi – независимые величины, поэтому коэффициент при каждом из них должен быть равен 0:

ln Ni + 1 + α + βEi = 0 ,

Ni =

 

1

.

exp (1

+ α + βEi )

 

 

Подставляя это выражение в условие постоянства числа частиц, исключаем коэффициент α:

Ni = N kexp (−βEi ) .

∑exp (−βEi )

i=1

Данная формула решает поставленную задачу. Физический смысл параметра β можно определить, воспользовавшись соотношениями между термодинамической вероятностью и энтропией (см. § 15). Этот параметр описывает тепловое равновесие и пропорционален обратной температуре:

β= kT1 .

Сучетом этого соотношения полученное распределение по уровням энергии совпадает с распределением Больцмана (14.29) для канонического ансамбля. Таким образом, распределение Больцмана – наиболее вероятное распределение частиц по энергиям.

Ответ. Распределение Больцмана.

Пример 14-2. Молекула может находиться на двух уровнях с энергиями 0 и 300 см–1. Какова вероятность того, что молекула будет находиться на верхнем уровне при 250 °С?

Решение. Надо применить распределение Больцмана, а для перевода

спектроскопической единицы энергии см–1 в Дж использовать множи-

тель hc (h = 6.63 10–34 Дж c, c = 3 1010 см с–1):

300 см–1 = 300 6.63 10–34 3 1010 = 5.97 10–21 Дж.

 

 

 

 

−

 

5.97 10−21

 

 

 

 

 

 

exp

 

 

 

 

 

 

 

 

 

N1

 

 

1.38 10

−23

523

 

 

=

 

 

 

 

 

 

 

= 0.304 .

N

 

 

 

 

5.97 10−21

 

 

 

 

 

 

 

 

 

 

 

1

+ exp

−

 

 

 

 

 

 

 

 

 

 

1.38 10

−23

523

 

 

 

 

 

 

 

 

 

 

 

Ответ. 0.304.

Пример 14-3. Молекула может находиться на уровне с энергией 0 или на одном из трех уровней с энергией E. При какой температуре:

а) все молекулы будут находиться на нижнем уровне,

220

Г л а в а 4. Статистическая термодинамика

б) число молекул на нижнем уровне будет равно числу молекул на верхних уровнях,

в) число молекул на нижнем уровне будет в три раза меньше, чем число молекул на верхних уровнях?

Решение. Для расчета числа молекул на нижнем уровне воспользуемся распределением Больцмана (14.29):

N 0

=

 

1

 

 

 

.

N

1 + 3exp

−

E

 

 

 

 

 

 

 

 

 

 

 

 

kT

 

а) N0 / N = 1; exp(–E/kT) = 0; T = 0. При понижении температуры молекулы накапливаются на нижнем уровне.

б) N0 / N = 1/2; exp(–E/kT) = 1/3; T = E / [k ln 3].

в) N0 / N = 1/4; exp(–E/kT) = 1; T = ∞. При высоких температурах молекулы равномерно распределены по уровням энергии, т.к. все больцмановские множители практически одинаковы и равны 1.

Ответ. а) T = 0; б) T = E / [k ln 3]; в) T = ∞.

Пример 14-4. В некоторой молекуле есть три электронных уровня энергии: 0, 1500 и 2800 см–1. Нижний уровень невырожден, средний – трехкратно вырожден, высший – пятикратно вырожден. Найдите среднюю электронную энергию молекулы (в см–1) и заселенность нижнего уровня при температуре 1900 К. Значение постоянной hc/k = 1.44 см К.

Решение. Используя распределение Больцмана, рассчитаем заселенности электронныхуровней, т.е. относительныеколичествамолекулнаэтихуровнях:

 

 

 

 

 

 

 

 

N 0

 

 

=

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

=

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

N

 

 

 

 

 

 

 

 

 

 

hcE1

 

 

 

 

 

 

 

 

hcE

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1 + 3exp −

 

 

 

 

 

 

+ 5exp

 

−

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

kT

 

 

kT

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

=

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

=

 

1

= 0.390

 

 

 

 

 

 

 

 

 

 

 

1.44

1500

 

 

 

 

 

 

 

1.44 2800

 

2.56

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1 + 3exp

 

−

 

 

 

 

 

 

 

+ 5exp −

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1900

 

 

 

 

 

1900

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(множитель hc использован для перевода см–1 в Дж);

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3exp

 

−

hcE1

 

 

 

 

 

 

 

 

 

 

 

 

 

3exp

 

−

 

1.44 1500

 

 

 

 

N1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

kT

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1900

 

 

 

 

 

=

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

=

 

 

 

 

 

 

 

 

 

 

 

 

 

 

= 0.376 ,

 

 

N

 

 

+ 3exp

 

−

hcE1

 

+ 5exp

 

−

 

hcE2

 

 

 

 

 

 

 

 

2.56

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

kT

 

 

kT

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5exp

 

−

hcE

2

 

 

 

 

 

 

 

 

 

 

 

 

 

5exp

 

−

1.44 2800

 

 

 

 

N 2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

kT

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1900

 

 

 

 

 

 

=

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

=

 

 

 

 

 

 

 

 

 

 

 

 

 

 

= 0.234 .

 

 

N

 

 

 

+ 3exp

 

−

hcE1

 

+ 5exp

 

−

 

hcE2

 

 

 

 

 

 

 

 

 

 

2.56

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

kT

 

 

kT

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Г л а в а 4. Статистическая термодинамика

221

Среднюю электронную энергию можно найти, сложив энергии отдельных уровней, умноженные на заселенности этих уровней:

E = ∑2

Ei

Ni

= 0 0.390 + 1500 0.376 + 2800 0.234 = 1219 см–1.

i=0

 

N

 

Ответ. 1219 см–1; 39.0%.

Пример 14-5. При нагревании любой термодинамической системы заселенность одних уровней увеличивается, а других – уменьшается. Используя распределение Больцмана, определите, какова должна быть энергия уровня для того, чтобы его заселенность увеличивалась с ростом температуры.

Решение. Заселенность – доля молекул, находящихся на определенном энергетическом уровне. По условию, производная от этой величины по температуре должна быть положительна:

d (Ni 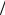N ) > 0 dT

В данном случае оказывается удобнее считать производную не самой заселенности, а ее логарифма (если функция – возрастающая, то ее логарифм тоже возрастает). Из распределения (14.29) следует:

 

 

 

Ni

 

 

 

 

Ei

− ln ∑exp

 

 

Ei

,

 

 

 

ln

 

 

 

 

= −

 

 

−

 

 

 

 

 

 

 

 

kT

 

 

 

 

 

 

 

N

 

 

 

 

 

i

 

 

 

 

kT

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ei

 

 

 

 

 

 

d ln (Ni

N )

 

 

Ei

 

 

 

 

 

∑Ei exp

−

 

 

 

 

 

 

 

Ei − E

 

 

 

 

 

 

1

 

 

kT

 

 

 

 

=

 

 

−

 

 

i

 

 

 

 

 

 

 

=

> 0 .

dT

 

 

kT 2

 

kT

2

 

 

 

 

 

Ei

 

 

kT 2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

∑exp

−

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i

 

 

 

kT

 

 

 

 

 

 

Во второй строчке мы использовали определение средней энергии (14.31). Таким образом, заселенность возрастает с ростом температуры для всех уровней, превышающих среднюю энергию системы.

Ответ. Ei > E .

ЗАДАЧИ

14-1. Найдите наиболее вероятное распределение 6 молекул по 3 ячейкам и рассчитайте термодинамическую вероятность этого распределения.

14-2. Рассчитайте фазовый объем для идеального газа, состоящего из N

3N

2

 

частиц с массой m. Гамильтониан системы: H ( p, q) = ∑

pi

.

 

i=1

2m

222

Г л а в а 4. Статистическая термодинамика

14-3. Молекула может находиться на двух уровнях с энергиями 0 и 100 см–1. Какова вероятность того, что молекула будет находиться на низшем уровне при 25 °С?

14-4. Молекула может находиться на двух уровнях с энергиями 0 и 600 см–1. При какой температуре на верхнем уровне будет в два раза меньше молекул, чем на нижнем?

14-5. Молекула может находиться на уровне с энергией 0 или на одном из трех уровней с энергией E. Найдите среднюю энергию молекул:

а) при очень низких температурах, б) при очень высоких температурах.

14-6. В некоторой молекуле есть два электронных уровня энергии, отстоящие друг от друга на 1000 см–1. Нижний уровень невырожден, верхний – трехкратно вырожден. Найдите среднюю электронную энергию молекулы (в см–1) при температуре 1200 К. Значение постоянной hc/k = 1.44 см К.

14-7. В некоторой молекуле есть три электронных уровня энергии: 0, 800 и 1700 см–1. Нижний уровень невырожден, средний – трехкратно вырожден, высший – пятикратно вырожден. Найдите среднюю электронную энергию молекулы (в см–1) и заселенность нижнего уровня при температуре 1300 К. Значение постоянной hc/k = 1.44 см К.

14-8. Вычислите вероятность нахождения атомарной серы в основном и первом возбужденном электронном состояниях при 1000 К с использованием следующих данных:

Электронный терм

Энергия (см–1)

 

Статистический вес

3P2

0

 

5

3P1

396.1

3

3P0

573.7

1

1D2

9238.6

5

14-9. Вычислите среднее значение электронной энергии атомарной серы при температуре 1000 К с использованием данных предыдущей задачи.

14-10. Молекула может находиться на трех энергетических уровнях: невырожденном, трехкратно вырожденном и пятикратно вырожденном. При некоторой температуре T на всех трех уровнях находится одинаковое число молекул. Рассчитайте энергии этих уровней (энергия основного состояния принимается равной 0).

14-11. В равновесной смеси α- и β-глюкозы содержание β-аномера равно 64% при температуре 25 °С. Оцените разность энергий между этими изомерами.

Г л а в а 4. Статистическая термодинамика

223

14-12. При охлаждении любой термодинамической системы заселенность одних уровней увеличивается, а других уменьшается. Используя распределение Больцмана, определите, какова должна быть энергия уровня для того, чтобы его заселенность увеличивалась с уменьшением температуры.

14-13. Рассчитайте наиболее вероятную скорость молекул углекислого газа при температуре 300 К.

14-14. Рассчитайте среднюю скорость атомов гелия при нормальных условиях.

14-15. При какой температуре средняя скорость молекул кислорода равна 500 м с–1?

14-16. При некоторых условиях средняя скорость молекул кислорода равна 400 м с–1. Чему равна средняя скорость молекул водорода при этих же условиях?

14-17. При температуре 25 °С средняя скорость молекул некоторого газа равна 274 м с–1. Чему равна средняя скорость молекул этого газа при температуре 250 °С?

14-18. Какова доля молекул массой m, имеющих скорость выше средней при температуре T? Зависит ли эта доля от массы молекул и температуры?

14-19. Пользуясь распределением Максвелла, рассчитайте среднюю кинетическую энергию движения молекул массой m при температуре T. Равна ли эта энергия кинетической энергии при средней скорости?

§15. Сумма по состояниям

истатистический интеграл

Согласно основному постулату статистической механики, должна существовать связь между функцией распределения равновесной системы и ее термодинамическими свойствами. Эта связь нагляднее всего проявляется в методе ячеек Больцмана. Равновесное состояние имеет максимальную термодинамическую вероятность; в то же время, согласно II закону, оно характеризуется максимальной энтропией, следовательно энтропия – возрастающая функция термодинамической вероятности:

S = f(W).

(15.1)

Для определения явного вида этой функции рассмотрим равновесную систему, состоящую из двух независимых подсистем. Общая термодинамическая вероятность равна произведению вероятностей, а общая энтропия – сумме энтропий отдельных подсистем:

W = W1 W2, S = S1 + S2.

(15.2)

224

Г л а в а 4. Статистическая термодинамика

(15.3)

(15.4)

(15.5)

(15.6)

(15.7)

(15.8)

отсюда следует, что энтропия пропорциональна натуральному логарифму термодинамической вероятности:

S = k ln W.

Это соотношение называют формулой Больцмана. Значение коэффициента k можно найти, рассмотрев изотермическое расширение идеального газа. Термодинамическая вероятность системы, состоящей из N молекул газа в объеме V, пропорциональна N-й степени объема:

W ~ V N.

При расширении газа от объема V1 до объема V2 изменение энтропии составит:

∆S = S2 − S1 = k ln (V2 N )− k ln (V1 N )= Nk ln V2 . V1

С другой стороны, из второго закона термодинамики следует, что при расширении одного моля идеального газа изменение энтропии:

∆S = R ln V2 . V1

Сравнивая (15.5) и (15.6), находим:

k =

R

.

 

 

N A

Коэффициент пропорциональности в формуле (15.3) – постоянная Больцмана.

Формула Больцмана позволяет объяснить существование остаточной энтропии (см. § 4) у некоторых веществ. В идеальном кристалле термодинамическая вероятность при температуре, близкой к абсолютному нулю, равна W = 1, поэтому такой кристалл имеет нулевую энтропию. Некоторые вещества, например CO или H2O, при любой температуре имеют термодинамическую вероятность W > 1 за счет того, что молекулы в кристалле могут иметь разные направления ориентации, поэтому энтропия таких веществ отличается от 0 даже вблизи абсолютного нуля1.

В классическом микроканоническом ансамбле энтропия определяется через фазовый объем Γ(E) по формуле, аналогичной формуле Больцмана:

S(E) = k ln Γ(E),

где k – постоянная Больцмана.

Можно доказать, что логарифм фазового объема обладает такими же свойствами, что и энтропия: он является экстенсивной величиной и

1 Остаточная энтропия CO составляет 5.0 Дж моль–1 К–1, H2O – 3.4 Дж моль–1 К–1.

Г л а в а 4. Статистическая термодинамика

225

имеет максимальное значение при равновесии. Аналогичным образом энтропию определяют через плотность энергетических состояний g(E), которая представляет собой нормировочный множитель функции распределения (14.16) микроканонического ансамбля:

S(E) = k ln g(E).

В статистической механике доказывается, что выражения (15.8) и (15.9) отличаются друг от друга на малую величину порядка k ln N. Определив энтропию как функцию энергии, можно рассчитать температуру:

 

∂S

=

1

 

 

 

 

 

T (E)

 

∂E V ,N

 

(15.9)

(15.10)

ивывести калорическое уравнение состояния E = E(T, V, N).

Вквантовом микроканоническом ансамбле энтропию также определяют через плотность состояний, которую рассчитывают непосредственно по энергетическому спектру системы.

Термодинамические свойства закрытых систем удобнее всего находить с помощью канонического ансамбля. Функции распределения – классическая (14.17) и квантовая (14.27) – позволяют рассчитать средние значения любых физических величин. Ключевую роль в этих расчетах играют нормировочные множители функций распределения – сум-

ма по состояниям и статистический интеграл.

Сумма по состояниям (синоним – статистическая сумма) – это нормировочный множитель квантовой функции распределения канони-

ческого ансамбля. Если известны уровни энергии системы Ei и их статистические веса (вырожденность) gi, то сумма по состояниям имеет вид:

Z (T ,V , N) = ∑gi

 

−

Ei

,

exp

 

 

 

i

 

 

kT

 

где T – температура, V – объем системы, N – число частиц.

Название «сумма по состояниям» отражает тот факт, что функция Z(T,V,N) представляет собой сумму больцмановских множителей для каждого из уровней энергии.

Нормировочный множитель классической функции распределения (14.17) называют статистическим интегралом. Он представляет собой объем фазового пространства, занимаемый каноническим ансамблем, и равен

 

 

H ( p, q)

 

∫exp

−

 

 

dpdq ,

kT

 

 

 

 

где интеграл берется по координатам и импульсам всех N частиц. Фазовый интеграл имеет кратность 6N и размерность (координата импульс)3N. С помощью фазового интеграла можно определить классическую сумму по состояниям, если воспользоваться формулой (14.21), устанавливаю-

(15.11)

(15.12)

226

Г л а в а 4. Статистическая термодинамика

щей связь между классической и квантовой статистической механикой. Классическая сумма по состояниям, выраженная через статистический интеграл, имеет вид:

 

 

 

1

 

 

 

H ( p, q)

 

(15.13)

Z (T,V , N) =

 

 

 

 

∫exp

−

 

 

dpdq .

h

3N

N !

kT

 

 

 

 

 

 

 

Здесь h – постоянная Планка. Множитель перед интегралом учитывает неразличимость частиц и квантовый принцип неопределенности. Статистическая сумма (15.13) безразмерна. Для большинства макроскопических систем классическая и квантовая суммы по состояниям практически совпадают.

Главное свойство суммы по состояниям заключается в том, что она содержит в себе всю термодинамическую информацию о системе. Ес-

ли каким-либо образом (аналитически или численно) удалось вычислить сумму по состояниям системы, то можно рассчитать все термодинамические функции и найти уравнение состояния этой системы. Таким образом,

Основная задача статистической термодинамики сводится к расчету сумм по состояниям термодинамических систем.

(15.14)

(15.15)

Свойства суммы по состояниям

Все нижеперечисленные свойства вытекают из определения (15.11). 1. Сумма по состояниям – безразмерная величина. Она зависит от температуры, объема и числа частиц: Z = Z(T,V,N). От температуры она зависит явным образом, а от объема и числа частиц зависят уровни

энергии: Ei = Ei(V,N).

2.Сумма по состояниям – не абсолютная величина: она определена

сточностью до постоянного множителя, который зависит от выбора уровня отсчета энергии. Если его сдвинуть, т.е. изменить все уровни энергии на одну и ту же величину: Ei → Ei + ε, то все больцмановские множители увеличатся (или уменьшатся) в одно и то же число раз, и во столько же раз изменится сумма по состояниям:

 

 

 

ε

Z →

Z exp

−

 

.

 

 

 

 

kT

Обычно за уровень отсчета принимают энергию системы при абсолютном нуле, U0.

3. При T → 0 все больцмановские множители стремятся к 0 за исключением того, который соответствует нижнему уровню энергии, поэтому сумма по состояниям стремится к статистическому весу этого уровня:

lim Z (T ) = g0 .

T →0

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности