
Основы физической химии_Ерёмин
.pdfГ л а в а 2. Приложения химической термодинамики |
127 |
7-34. Известно, что теплоемкость насыщенного пара может быть и положительной и отрицательной величиной. Предложите физическую интерпретацию такого факта.
7-35. Покажите, как изменяется с температурой объем пара, находящегося в равновесии с жидкостью. Укажите принятые допущения.
7-36. Покажите, как зависит от температуры энтальпия фазового перехода вдоль кривой фазового равновесия:
а) при равновесии конденсированной фазы с паром (идеальным газом);
б) при равновесии двух конденсированных фаз (∆V = const).
7-37. Покажите, что в тройной точке
(V |
|
− V |
|
) |
dp23 |
+ (V |
|
− V ) |
dp13 |
+ (V |
− V |
|
) |
dp12 |
= 0 . |
|
|
dT |
|
dT |
|
dT |
|||||||||
|
2 |
|
3 |
|
|
3 |
1 |
1 |
|
2 |
|
|
7-38. Постройте фазовую диаграмму бензола вблизи тройной точки при 36 Торр и 5.50 °C, используя следующие данные:
∆плHm = 10.6 кДж моль–1,
ρтв = 0.891 г см–3,
∆испHm = 30.8 кДж моль–1,
ρж = 0.879 г см–3.
§8. Фазовые равновесия
вдвухкомпонентных системах
Общие и частные условия равновесия, сформулированные в предыдущей главе, справедливы для систем любой компонентности. Поэтому те подходы, которые были использованы при расчетах фазовых равновесий в однокомпонентных системах, справедливы и для многокомпонентных систем.
I. Расчет фазовых равновесий в бинарных системах, исходя из общего условия равновесия (min G)
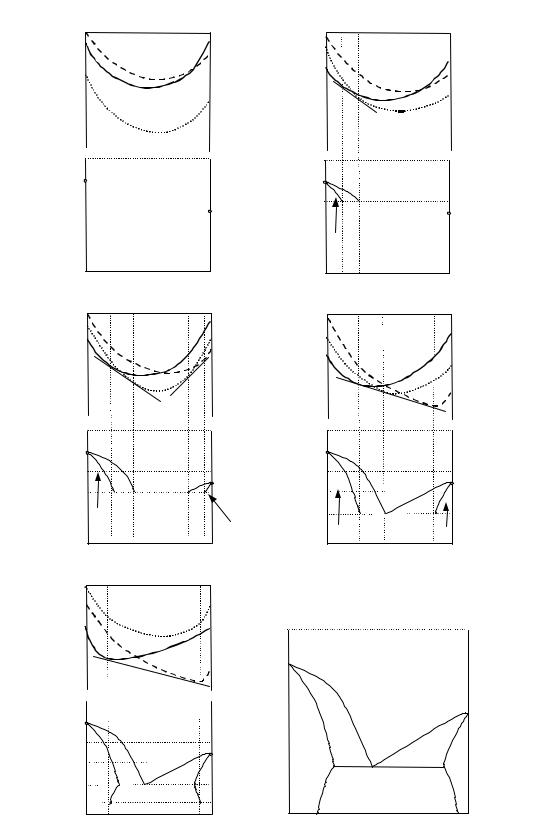
Поиск минимума энергии Гиббса системы положен в основу алгоритма расчета фазовых равновесий во всех современных электронных базах термодинамических данных. Изложение математического аппарата таких расчетов выходит за рамки настоящего издания. Но сам алгоритм расчета можно наглядно представить с помощью диаграмм Гиб-
бса–Розебома (рис. 8.1).
128 |
(а) |
|
Г л а в а 2. Приложения химической термодинамики |
|
|||||
|
x→ |
|
(б) |
|
x→ |
|
|
||
G1o,m (s2 ) |
|
|
G2o,m (s1) |
|
|
|
|
||
|
|
|
G1o,m (s2 ) |
|
|
|
|
||
G1o,m (s1 ) |
|
|
|
G2o,m (s2 ) |
o |
|
|
|
G2o,m (s1) |
|
|
|
|
|
G1,m (l) |
|
|
|
|
o |
|
|
|
|
G1o,m (s1) |
|
|
|
G2o,m (s2 ) |
G1,m (l) |
|
|
|
|
|
|
|
|
|
|
|
|
|
G2o,m (l) |
|
|
|
|
G2o,m (l) |
T1 |
|
|
|
|
T1 |
|
|
|
|
T1,пл |
|
|
|
|
|
|
l |
|
|
|
|
l |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T2,пл |
T2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s1 |
|
|
|
|
0 |
(в) |
|
|
1 |
0 xs1 |
xl |
|
|
1 |
|
|
x→ |
|
(г) |
x→ |
|
|
||
|
|
|
|
|
|
||||
|
|
|
G2o,m (s1 ) |
G1o,m (s2 ) |
|
|
|||
G1o,m (s2 ) |
|
|
|
|
G2o,m (s1 ) |
||||
o |
|
|
|
G2o,m (l) |
G1o,m (l) |
|
|
|
|
G1,m (l) |
|
|
|
o |
o |
|
|
|
|
|
|
|
|
G2,m (s2 ) |
|
|
|
|
|
G1o,m (s1) |
|
|
|
G1,m (s1 ) |
|
|
|
|
|
|
|
|
|
|
|
|
G2o,m (l) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G2o,m (s2 ) |
T1 |
|
|
|
T1 |
|
|
|
|
|
|
|
|
|
l |
|
|
l |
|
|
|
|
|
|
|
|
|
|
||
T2 |
|
|
|
T2 |
|
|
|
|
|
T3 |
|
|
|
T3 |
|
|
|
|
|
|
s1 |
|
s2 |
T4 |
|
|
|
|
|
|
|
|
|
s1 |
|
|
s2 |
|
|
0 |
xs1 |
xl1 |
xl2 xs2 1 |
|
|
|
|||
0 |
E |
E |
E |
1 |
|||||
|
(д) |
|
|
|
xs1 |
xl |
xs 2 |
||
G1o,m (l) |
|
x→ |
G2o,m (l) |
|
|
|
|
|
|
G1o,m (s2 ) |
|
|
|
(е) |
|
|
|
|
|
G1o,m (s1) |
|
|
|
|
|
|
|
|
|
|
|
|
G2o,m (s1 ) |
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
G2o,m (s2 ) |
|
|
|
|
|
l
T1 





















 l
l 
T2 |
s1 |
|
|
||
T3 |
s2 |
|
T4 |
||
|
||
T5 |
|
Рис. 8.1 |
Диаграммы Гиббса-Розебома |

Г л а в а 2. Приложения химической термодинамики |
129 |
Рассмотрим бинарную систему, компоненты которой ограниченно растворимы в твердом состоянии и не образуют соединений. Пусть для первого компонента более устойчивой является структура s1, а для
второго – s2. Обозначим образуемые ими твердые растворы как s1 и s2 соответственно, жидкость – l, а количества фаз как ns1, ns2, nl. В
предыдущем параграфе отмечалось, что для расчета равновесий необходимо знать свойства каждой фазы во всей области изменения переменных, поэтому на рис. 8.1. схематично изображены концентрационные зависимости энергий Гиббса всех трех фаз рассматриваемой системы при различных температурах. По оси ординат отложены абсолютные значения мольных функций G в зависимости от состава1. Давление в системе постоянно.
Предположим, что при температуре T1 (рис. 8.1.а) кривая энергии Гиббса жидкой фазы расположена ниже остальных кривых. Это значит, что при любом составе (x) минимальное значение общей энергии Гиббса системы
G(x) = ns1Gms1 + ns2Gms2 + nlGml
достигается при нулевых количествах твердых растворов s1 и s2, т.е. при температуре T1 во всей области составов устойчива жидкая фаза.
При понижении температуры точки Gio,m (T ) , соответствующие
мольным свойствам чистых компонентов, перемещаются вверх (энергия Гиббса становится более положительной при уменьшении температуры, см. рис. 5.2). Скорость движения i-ой фигуративной точки равна:
|
∂G o |
|
|
|
|
i,m |
|
= −Sio,m . |
|
∂T |
||||
|
|
|
||
|
|
p |
|
Так как энтропии чистых компонентов с разной структурой различны, будут отличаться и скорости движения точек по оси ординат. При температурах плавления Tпл,1 и Tпл,2 мольные энергии Гиббса твердых и жидких компонентов станут одинаковыми, точки совместятся.
На рис. 8.1.б представлены концентрационные зависимости Gi(x) при T2, где Tпл,2 < T < Tпл,1. Как видно из рисунка, при составах 0 < x < xs1 минимуму энергии Гиббса соответствуют нулевые количества твердого
раствора s2 и l, а при составах xl < x < 1 – отсутствие в равновесной смеси твердых растворов. В интервале составов xs1< x < xl возможно при-
сутствие жидкости и раствора s1, причем составы этих растворов определяются общей касательной к кривым Gs1(x) и Gl(x), а количества их в
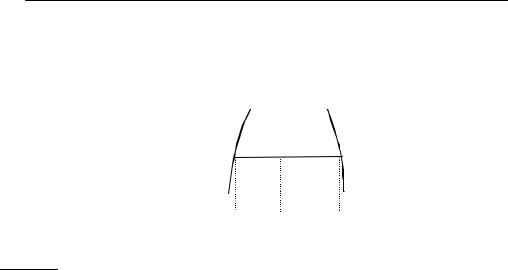
равновесной смеси – правилом рычага (рис. 8.2):
(8.1)
(8.2)
1 Так как свойства раствора отсчитывают относительно единого уровня для всех компонентов, переход от абсолютных значений энергии Гиббса к функциям смешения не отразится на положении минимума G относительно оси абсцисс.
130Г л а в а 2. Приложения химической термодинамики
Количества сосуществующих фаз ′ и ″ в гетерогенной смеси обратно пропорциональны длинам отрезков аа′ и аа″.
|
a′ |
a |
|
a″ |
|
|
|
|
|
|
|
|
0 x′ |
x |
x″ |
1 |
|
Рис. 8.2
(8.3.а)
(8.3.б)
Иллюстрация правила рычага
Это правило является прямым следствием уравнения материального баланса в бинарной системе:
n1 = ns1 x1s1 + ns2 x1s2 + nl x1l,
n2 = ns1 x2s1 + ns2 x2s2 + nl x2l,
где ni – количество i-го компонента, xi j – мольная доля i-го компонента в j-ом (твердом или жидком) растворе.
При температуре T3, меньшей Tпл,2 и Tпл,1 (рис. 8.1.в), пересекаются линии Gs1(x), Gl(x) и Gs2(x), Gl(x). Построив общие касательные к этим
кривым, можно определить составы равновесно сосуществующих фаз s1/l и s2/l. Твердые растворы s1 и s2 будут устойчивы в областях 0 s1, s2 1, соответственно, а жидкость – при составах xl1 xl2. Дальнейшее понижение температуры до T4 может привести к ситуации, изображенной на рис. 8.1.г. При этой температуре все три кривые имеют общую касательную, минимум энергии Гиббса наблюдается при нали-
чии всех трех фаз состава |
xE , |
xE |
, |
xE , т.е. реализуется эвтектическая |
|
s |
s |
|
l |
|
1 |
2 |
|
|
точка (число степеней свободы системы равно 0). При температуре T5 (рис. 8.1.д) жидкость становится неустойчивой относительно твердых растворов во всей области составов, а границы гетерогенной области (s1+s2) определяются положением общей касательной к кривым Gs1(x) и Gs2(x). На рис. 8.1.е представлена полученная фазовая диаграмма бинарной системы.
II. Расчет фазовых равновесий из частных условий равновесия
Фазовые равновесия можно также рассчитывать, используя условие равенства химических потенциалов компонентов в сосуществующих фазах. Для этого необходимо задать температурно-концентрационные зависимости химических потенциалов компонентов каждой фазы (т.е.
термодинамические модели фаз, см. § 6). Например, для рассмотрен-
Г л а в а 2. Приложения химической термодинамики |
131 |
ной выше бинарной системы условие равновесия жидкости l с твердым раствором s1 можно представить в виде системы уравнений:
|
|
(x |
s1 |
,T ) = µ A,1 (x |
l |
,T ), |
µ A ,s1 |
|
|
||||
|
|
(xs1 |
,T ) = µ B,1 (x l |
,T ), |
||
µ B,s |
1 |
|||||
|
|
|
|
|
|
|
|
o |
+ RTln(1 − x |
s1 |
|
ex |
|
o |
|
l |
ex |
µ A ,s1 |
|
) + µ A,s1 |
= µ A ,l + RTln(1 − x |
|
) + µ A,l , |
|||||
|
|
+ RT ln x s1 + µ ex |
= µ o |
+ RT ln x l |
+ µ ex . |
|||||
µ o |
||||||||||
|
B,s 1 |
|
|
B,s1 |
|
B,l |
|
B,l |
|
|
Аналогичные системы уравнений записывают и для остальных пар фаз. В результате решения получают набор линий фазовых равновесий, после чего отделяют стабильные равновесия от метастабильных. Аналитическое решение задачи возможно только для систем с идеальными растворами (Gex = 0) (см. пример 8-1). В остальных случаях приходится решать систему нелинейных уравнений численными методами.
Если воспользоваться условиями равновесия в дифференциальной форме (индексы ′ и ″ относятся к сосуществующим фазам)
dµ′ |
= dµ′′ , |
dµ′ |
= dµ′′ |
, |
1 |
1 |
2 |
2 |
|
то можно получить обобщенное уравнение Ван-дер-Ваальса, которое описывает любые фазовые равновесия в бинарных системах:
|
|
∂V ′ |
|
|
|
|
|
∂S ′ |
|
V ′′ − V ′ − (x′′ − x′) |
dp |
+ S ′′ − S ′ − (x′′ − x′) |
dT = |
||||||
|
|
∂x′ |
|
|
|
|
|
∂x′ |
|
|
|
p,T |
|
|
|
|
p,T |
||
|
|
|
∂ 2G′ |
dx′ |
|
|
|||
|
= (x′′ − x′) |
|
2 |
|
|
|
|||
|
|
|
∂x′ |
|
|
|
|
||
|
|
|
|
|
p,T |
|
|
|
|
или |
|
|
|
|
|
|
|
|
|
|
|
∂V ′′ |
|
|
|
|
|
∂S ′′ |
|
V ′′ − V ′ − (x′′ − x′) |
dp |
+ S ′′ − S ′ − (x′′ − x′) |
dT = |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
∂x′′ p,T |
|
|
|
|
|
∂x′′ p,T |
|
|
|
|
∂ 2G′′ |
dx′′ |
|
|
|||
|
= (x′′ − x′) |
|
|
2 |
|
|
|
||
|
|
|
∂x′′ |
|
|
|
|
||
|
|
|
|
p,T |
|
|
|
||
Для вывода некоторых практически важных соотношений более удобной является следующая форма записи этих уравнений:
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ 1′′ |
|
|
∂ 1′ |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
(V1′ − V1′′)dp − (S1′ − S1′′)dT = |
|
|
|
dx′′ − |
|
|
dx′ = |
|||||||||||||
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
∂x′′ p,T |
|
∂x′ |
p,T |
|
|||
|
|
|
|
|
∂ 2G |
′ |
dx′ − |
|
∂ 2G′′ |
dx′′ |
|
|
||||||||
|
|
|
|
= x′ |
|
|
|
2 |
|
|
x′′ |
|
2 |
|
|
|
||||
|
|
|
|
|
∂x′ |
|
|
|
|
∂x′′ |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
p,T |
|
|
|
p,T |
|
|
|
|
|||||
(8.4.а)
(8.4.б)
(8.5.а)
(8.5.б)
(8.6.а)
или

132 |
|
Г л а в а 2. Приложения химической термодинамики |
||||||||||||||
|
|
|
( |
|
− |
|
)dp − ( |
|
− |
|
)dT = |
|||||
|
|
|
V2′ |
V2′′ |
S2′ |
S2′′ |
||||||||||
|
|
|
∂µ′′ |
|
|
∂µ′ |
|
|
||||||||
(8.6.б) |
= |
2 |
|
dx′′ − |
2 |
|
dx′ = |
|||||||||
∂x′′ |
∂x′ |
|||||||||||||||
|
|
|
p,T |
|
p,T |
|
||||||||||
= − (1 |
|
∂ 2G′ |
dx′ + (1 |
|
∂ 2G′′ |
dx′′ |
||||
− x′) |
|
2 |
|
− x′′) |
|
2 |
|
|||
|
|
∂x′ |
|
|
|
∂x′′ |
|
|
||
|
|
|
p,T |
|
|
|
p,T |
|
||
(8.7.а)
(8.7.б)
(8.8.а)
(8.8.б)
Чтобы использовать выражения (8.5–8.6) для расчетов равновесий, необходимо конкретизировать вид частных производных химических потенциалов по мольной доле второго компонента. В общем случае
|
∂µ |
1 |
|
|
|
∂ 2G |
|
|
RT |
|
∂µ ex |
||||||||
|
|
|
|
|
|
= −x |
|
= − |
|
|
|
|
+ |
1 |
, |
||||
|
∂x p,T |
|
|
|
|
|
|
|
|||||||||||
∂x2 |
|
|
1 − x |
|
|
∂x |
p,T |
||||||||||||
∂µ |
2 |
|
|
|
∂ 2G |
|
|
RT |
|
|
∂µ ex |
||||||||
|
|
|
|
|
= (1 − x) |
|
|
= |
|
|
+ |
|
2 |
|
. |
||||
|
∂x p,T |
|
|
|
|
|
|||||||||||||
|
|
∂x2 |
|
|
|
x |
|
|
∂x |
|
p,T |
||||||||
В случае идеальных растворов:
∂µ1 |
|
|
|
∂ 2G |
|
|
RT |
|
||||||
|
|
|
= −x |
|
|
|
= − |
|
|
|
|
, |
||
|
|
|
|
|
|
|
||||||||
∂x |
|
|
∂x |
2 |
|
1 − x |
|
|||||||
|
p,T |
|
|
|
|
|
|
|||||||
∂µ 2 |
|
|
|
|
∂ 2G |
|
|
RT |
|
|||||
|
|
|
|
= (1 |
− x) |
|
|
= |
|
|
. |
|||
|
|
|
|
|
|
|||||||||
∂x |
|
|
|
∂x |
2 |
|
|
x |
|
|||||
|
p,T |
|
|
|
|
|
|
|
||||||
Далее приведены некоторые полезные соотношения, описывающие фазовые равновесия в бинарных системах. Эти соотношения при определенных допущениях могут быть получены из уравнений Ван-дер- Ваальса либо при рассмотрении частных равновесий1.
Равновесие жидкость – пар. Законы Д.П. Коновалова
Рассмотрим двухфазную систему, состоящую из двух летучих жидкостей и их паров. Обозначим жидкость индексом ′, а паровую фазу – индексом ″. Примем, что температура системы постоянна, T = const. В этом случае уравнение (8.5.а) преобразуется к виду:
1 Традиционно во многих учебных пособиях используют именно частные равновесия. В настоящем издании показано, как те же самые выражения получаются из обобщенного уравнения.
Г л а в а 2. Приложения химической термодинамики |
133 |
|||||||||||
|
|
|
|
|
|
∂ 2G′ |
|
|
|
|
||
|
|
|
|
|
(x′′ − x′′) |
|
2 |
|
|
|
|
|
|
∂p |
|
|
|
∂x′ |
|
|
|
|
|
||
= |
|
|
|
p,T |
|
, |
(8.9) |
|
||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
∂V ′ |
|
||||||
|
∂x′ T |
|
|
|
|
|
|
|
||||
|
|
|
|
V ′′ − V ′ − (x′′ − x′) |
∂x′ |
|
|
|
|
|||
|
|
|
|
|
|
|
|
p,T |
|
|
|
|
где левая часть описывает зависимость общего давления в газовой фазе от состава жидкости. Если учесть, что
•изменение объема жидкости с составом, (∂V′/∂x)p,T, мало по сравнению с разностью объемов паровой и жидкой фаз,
•вдали от критических условий можно пренебречь удельным объемом жидкости по сравнению с объемом пара V ′ << V ′′ ,
•в состоянии устойчивого равновесия энергия Гиббса системы ми-
нимальна, т.е. |
|
∂ |
2 |
G |
|
> |
0 , |
||
|
|
|
|||||||
|
|
∂x |
2 |
|
|
|
|||
|
|
|
p,T |
|
|
||||
то знак производной |
|
|
∂p |
|
будет определяться знаком разности |
||||
|
|
||||||||
|
|
|
|
|
|
∂x′ T |
|
||
(x″ − x′). При
x″ > x′, |
∂p |
|
> 0, |
|
|||
∂x′ T |
|||
x″ < x′, |
∂p |
|
< 0, |
|
|||
∂x′ T |
|||
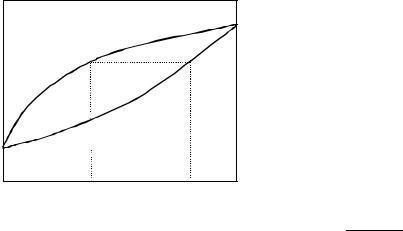
что выражает первый закон Коновалова (см. рис. 8.3):
Насыщенный пар содержит больше (по сравнению с раствором) того компонента, увеличение концентрации которого в растворе повышает общее давление пара, т.е. понижает температуру кипения смеси при данном давлении.
(8.10.а)
(8.10.б)
p |
|
|
|
|
l |
|
|
|
g |
|
|
0 |
xl |
xg |
1 |
|
Иллюстрация первого закона Коновалова |
Рис. 8.3 |
|
134 Г л а в а 2. Приложения химической термодинамики
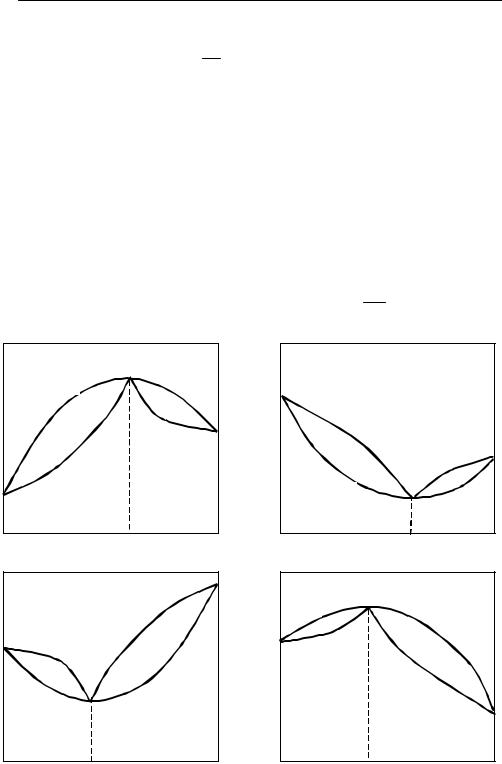
Если x″ = x′, то ∂p = 0, таким образом, приходим к формули-∂x′ T
ровке второго закона Коновалова:
Точки максимума и минимума на кривой общего давления пара отвечают раствору, состав которого одинаков с составом равновесного с ним пара.
Растворы, у которых составы пара и жидкости совпадают, называ-
ются азеотропами (см. рис. 8.4).
Из обобщенного уравнения Ван-дер-Ваальса следует и третий за-
кон Коновалова:
В изотермических (или изобарических) условиях составы рас-
dx′
твора и пара изменяются симбатно, т.е. dx′′ > 0 .
p |
T |
|
|
l |
|
|
g |
|
g |
|
l |
x → |
x → |
p |
T |
|
|
l |
g |
|
|
|
l |
|
g |
x → |
x → |
Рис. 8.4 |
T–x и p–x диаграммы бинарных систем с верхним и нижним азеотропом, |
|
g – паровая фаза, l – жидкость |
|

Г л а в а 2. Приложения химической термодинамики |
135 |
Законы Коновалова получены эмпирически, но они также могут быть выведены как следствия обобщенного уравнения фазовых равновесий Ван-дер-Ваальса.
Равновесие конденсированных фаз. Уравнения Планка – Ван Лаара и Шредера
Предположим, что чистый компонент В (фаза ′) находится в равновесии с насыщенным раствором (″). Рассмотрим случаи постоянства (а) давления, (б) температуры.
а) p = const
В этом случае
•dp = 0,
• x′ = 1, dx′ = 0, |
S ′ |
= S o |
, |
|
B |
B,тв |
|
• |
растворимость компонента B равна мольной доле В в растворе (x″), |
|||
• |
в идеальном растворе |
|
→ H o |
при x → 1. 1 |
H ′′ |
||||
|
|
B |
B,ж |
|
С учетом принятых допущений уравнение Ван-дер-Ваальса упрощается
|
|
|
|
|
|
|
|
|
|
o |
|
|
|
|
|
′′ |
|
|
|
|
RT |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
∂µ B |
|
|
|
|
|
|
|||||||
0 − (SB′ − SB′′ )dT = (SB′′ − SB,тв )dT = |
|
|
|
|
|
|
dx′′ = |
|
dx′′ = RTdlnx′′ |
||||||||||||||||
∂x′′ |
|
|
x′′ |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B p,T |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
− |
S o |
|
|
|
− H o |
|
|
|
|
|
|
|||||
|
|
|
|
∂ ln x |
|
|
S ′′ |
|
H ′′ |
|
|
|
∆ плH B |
|
|||||||||||
|
|
|
= |
|
B |
B,тв |
= |
|
B |
|
|
|
|
B,тв |
= |
, |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
RT |
|
|
|
RT 2 |
|
RT 2 |
|
|||||||||||||
|
|
|
|
∂T p |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Уравнение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
∂ln x |
|
|
= |
∆ |
плH B |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
∂T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
RT |
2 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
p,насыщ |
|
|
|
|
|
|
|
|
|
|||||||
получило название уравнение Шредера. Оно описывает изменение растворимости твердого вещества с изменением температуры.
Интегрируя уравнение Шредера в предположении независимости энтальпии от температуры, получаем уравнение, описывающее кривую кристаллизации компонента В:
ln x = ∆ плH B (T − Tпл ) . RTплT
1 |
|
– H o |
= |
|
− H o |
+ H o |
− H o |
= |
H ex |
|
|
|
|
, где ∆плHB – |
H ′′ |
H ′′ |
+ ∆ |
пл |
H |
B |
|||||||||
|
B |
B,тв |
|
B |
B,ж |
B,ж |
B,тв |
|
B |
|
|
|
теплота плавления переохлажденной жидкости, а H Bex → 0 при xВ → 1.
(8.11.а)
(8.11.б)
136 |
|
Г л а в а 2. Приложения химической термодинамики |
||||
T |
|
|
|
|
|
Аналогичное уравнение можно |
|
|
|
|
|
записать и для другого компонента |
|
|
|
|
|
|
раствора. Две кривые кристаллиза- |
|
|
|
l |
|
|
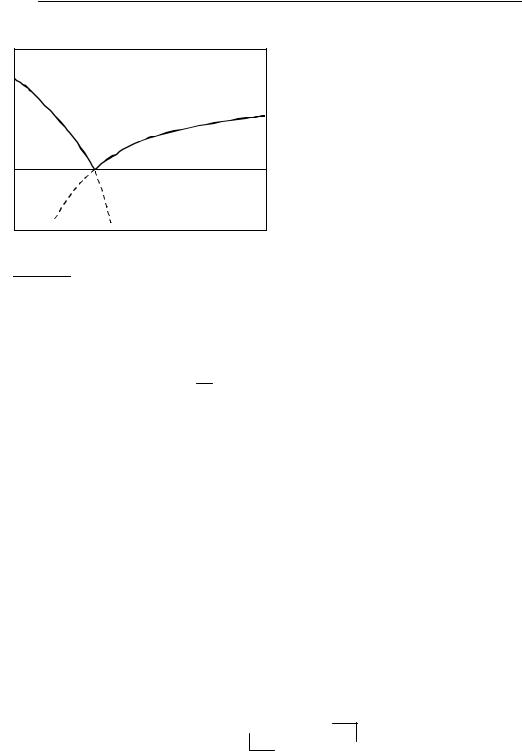
ции |
пересекаются в эвтектической |
|
|
|
|
|
точке (см. рис. 8.5) |
|
|
|
|
l + B |
|
|
Выводы из уравнения Шредера: |
A + l |
|
|
|
• |
так как ∆плH > 0, то раствори- |
|
|
|
|
|
|||
|
|
|
|
|
мость твердых веществ в жидкости |
|
|
|
|
|
|
увеличиваетсясростомтемпературы, |
|
|
|
A + B |
|
|
• вещества с более высокой тем- |
|
А |
|
x→ |
|
В |
пературой плавления менее раство- |
|
|
|
римы, |
||||
Рис. 8.5 |
|
T–x-диаграмма бинарной |
|
• растворимость вещества во всех |
||
системы с простой эвтектикой |
растворителях, с которыми оно об- |
|||||
|
|
|
|
|
разует идеальный раствор, не зави- |
|
|
|
|
|
|
сит от природы растворителя. |
|
|
|
б) T = const |
|
|
|
|
|
|
Преобразуяобобщенное уравнениеВан-дер-Ваальсасучетомтого, что |
||||
|
• |
dT = 0, |
= V o |
|
|
|
|
• |
x′ = 1, dx′ = 0, V ′ |
, |
|
|
|
|
|
B |
B,тв |
|
|
|
|
• x″ – растворимость второго компонента, |
|||||
|
получаем уравнение Планка–Ван Лаара |
|||||
(8.12) |
|
∂ ln x |
= − |
∆ плVB |
, |
|
∂p T ,насыщ |
|
|||
RT |
где ∆плVB – изменение объема компонента В при неравновесном плав-
лении (ниже Tпл).
Уравнение Планка–Ван Лаара описывает влияние давления на растворимость твердого вещества. Согласно уравнению (8.12), с повышением давления должна уменьшаться растворимость веществ, у которых мольный объем жидкости больше мольного объема твердой фазы.
С помощью уравнений (8.5–8.6) можно также получить все выражения, описывающие коллигативные свойства растворов (см.§ 6). Основная проблема, связанная с использованием дифференциальных уравнений фазовых равновесий (в том числе, обобщенного уравнения Ван- дер-Ваальса) – получение их интегральной формы.
ПРИМЕРЫ
Пример 8-1. Получите аналитическое выражение, описывающее кривую ликвидус в бинарной системе с неограниченной растворимостью компонентов в твердом и жидком состоянии. Растворы можно считать идеальными.
