
Основы физической химии_Ерёмин
.pdf
|
|
|
Г л а в а 1. Основы химической термодинамики |
|
|
|
17 |
||||||||
ние. Сами уравнения состояния нельзя вывести методами классической |
|
|
|||||||||||||
термодинамики, но их можно определить экспериментально. |
|
|
|
|
|||||||||||
Самым простым уравнением состояния описывается идеальный газ – |
|
|
|||||||||||||
совокупность невзаимодействующих частиц точечного размера: |
|
|
|
||||||||||||
|
|
|
|
|
|
|
pV = nRT, |
|
|
|
|
|
(1.4.а) |
|
|
где R – универсальная газовая постоянная, или |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
pVm = RT, |
|
|
|
|
|
(1.4.б) |
|
|
где Vm = V/n – мольный объем газа (см. рис. 1.1). |
|
|
|
|
|
||||||||||
Реальные газы лишь прибли- |
|
|
|
|
|
|
|
||||||||
женно |
описываются |
уравнением |
|
|
|
|
|
|
|
||||||
состояния идеального газа. При вы- |
|
|
|
|
|
|
|
||||||||
соких давлениях и низких темпера- |
|
|
|
|
|
|
|
||||||||
турах (особенно когда газ близок к |
|
|
|
|
|
|
|
||||||||
конденсации) отклонения от иде- |
|
|
|
|
|
|
|
||||||||
ального поведения становятся зна- |
|
p |
|
|
|
|
|
||||||||
чительными. |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Удобной мерой неидеальности |
|
|
|
|
|
|
|
||||||||
является |
фактор |
сжимаемости |
|
|
|
|
|
|
|
||||||
Z = pVm/RT, поскольку для идеаль- |
|
|
|
|
|
|
|
||||||||
ного газа Z = 1 при любых условиях. |
|
|
|
|
|
|
|
||||||||
На рис. 1.2 представлены факторы |
|
|
|
|
|
|
|
||||||||
сжимаемости некоторых реальных |
|
|
|
V |
|
|
|
||||||||
газов как функции давления при |
Изотермы идеального газа |
|
Рис. 1.1 |
|
|||||||||||
298 К |
(пунктир |
соответствует |
иде- |
|
22,0. |
|
|
|
|
|
|||||
альному газу). Из рисунка видно, |
|
|
|
|
|
|
|||||||||
что |
при |
высоких |
давлениях |
для |
|
11,8. |
|
|
|
|
|
||||
всех |
газов Z > 1, |
т.е. их труднее |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|||||||||
сжать, чем идеальный газ, посколь- |
//RTRT |
11,6. |
|
|
N2 |
|
|
||||||||
ку в этой области преобладают силы |
1. |
|
|
|
|
|
|||||||||
межмолекулярного |
отталкивания. |
|
|
|
|
|
|||||||||
m |
|
|
|
He |
|||||||||||
m |
1,4 |
|
|
|
|||||||||||
При низких давлениях для некото- |
pV |
1. |
H2 |
|
|
|
|
||||||||
ZZ== |
|
|
|
|
|||||||||||
рых |
газов |
Z < 1, |
что |
объясняется |
1,2 |
|
|
O2 |
|
|
|||||
|
|
|
|
|
|||||||||||
преобладанием |
межмолекулярного |
|
1. |
|
|
|
|
|
|||||||
притяжения. При p → 0 эффект |
|
1,0 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|||||||||
межмолекулярного |
взаимодействия |
|
00,8. |
CH4 |
|
|
|
|
|||||||
исчезает, потому что длина свобод- |
|
|
|
|
|
|
|||||||||
|
0. |
|
|
|
|
|
|||||||||
ного |
|
пробега молекул |
становится |
|
200 |
|
600 |
|
1000 |
||||||
|
|
0,600 |
400 |
800 |
|||||||||||
много |
больше |
расстояния |
между |
|
|
|
p, бар |
|
|
||||||
частицами, и для всех газов Z → 1, |
|
Зависимость фактора |
|
Рис. 1.2 |
|
||||||||||
т.е. в этих условиях все газы ведут |
сжимаемости некоторых |
|
|
|
|||||||||||
себя почти идеально. |
|
|
|
газов от давления при 298 K |
|
|
|
||||||||
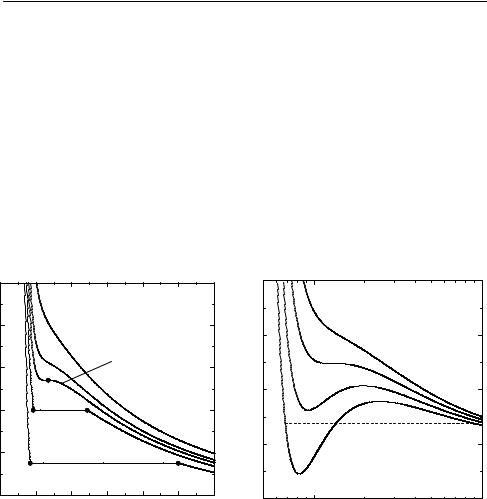
18Г л а в а 1. Основы химической термодинамики
Вотличие от изотерм идеального газа (рис. 1.1), на изотермах реальных газов (рис. 1.3.а) наблюдаются горизонтальные участки, соответствующие процессу конденсации газа в жидкость. Давление, соответствующее горизонтальным участкам, когда жидкость и пар находятся в равновесии, называют давлением насыщенного пара жидкости при данной температуре. При повышении температуры длина
этих участков уменьшается, и при критической температуре Tc на изотерме наблюдается точка перегиба – критическая точка. Она ха-
рактеризуется критической температурой Tc, критическим давлением pc и критическим мольным объемом Vc. Критические константы некоторых газов приведены в приложении (табл. П-2).
а) |
|
|
|
|
|
|
|
б) |
|
|
|
|
120 |
|
|
|
|
|
|
|
150 |
|
|
|
|
|
|
60oC |
|
|
|
|
|
|
|
1.1 T |
|
|
100 |
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
80 |
|
40oC |
31.04 oC (Tc) |
|
бар,p |
|
|
Tc |
|
|
||
|
20oC |
|
|
|
|
|
|
|
|
|
||
бар,p |
|
|
|
|
|
50 |
|
0.9 Tc |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
60 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
3 |
|
2 |
40 |
|
0oC |
|
|
|
|
|
0 |
|
0.8 Tc |
|
|
|
|
|
|
|
|
|
|
|
|
|||
20 |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
|
-50 |
1 |
2 |
5 |
10 |
0.0 |
|
0.5 |
||||||||||
|
|
V, л моль−1 |
|
|
|
|
|
V, л моль−1 |
|
|
||
Рис. 1.3 |
Изотермы CO2: а) экспериментальные; |
|
б) рассчитанные по уравнению Ван-дер-Ваальса |
|
Для описания реальных газов используют более сложные уравнения состояния, в которых межмолекулярные взаимодействия учитывают с помощью эмпирических параметров, индивидуальных для каждого газа. Некоторые уравнения состояния реальных газов приведены в табл. 1.1. Известно более ста подобных уравнений, отличающихся числом параметров, степенью точности и областью применимости. Выяснилось, что ни одно из уравнений состояния, содержащих менее 5 индивидуальных постоянных, не является достаточно точным для описания реальных газов в широком диапазоне p, V, T, и все эти уравнения оказались непригодными в области конденсации газов. Из простых уравнений с двумя индивидуальными параметрами удовлетворительные результаты дают уравнения Бертло и Дитеричи
(табл. 1.1).

|
|
Таблица 1.1 |
|
|
|
|
Уравнения состояния реальных газов (для одного моля) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уравнение |
|
Обычная форма |
|
|
|
Приведенная форма |
|
|
|
|
pc |
|
|
|
|
|
|
|
|
Tc |
|
|
Vc |
|
|
|
|
Zc |
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Ван-дер-Ваальса (1873) |
|
|
|
p = |
|
RT |
|
|
|
− |
|
a |
|
|
|
|
|
|
|
pr |
= |
|
8Tr |
− |
|
3 |
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
8a |
|
|
3b |
|
3 |
= 0.375 |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
V − b |
|
V 2 |
|
|
|
|
|
|
|
|
− 1 |
|
|
|
|
|
|
|
|
27b 2 |
|
|
|
|
|
27bR |
|
|
8 |
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3V |
|
V 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дитеричи (1898) |
|
|
|
|
RT |
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
Tr e |
2− 2/T V |
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
a |
|
|
|
2 |
|
|
|
||||||||||||||||||
|
|
|
|
p = |
|
|
|
|
|
|
|
|
exp − |
|
|
|
|
|
|
|
|
|
|
pr |
|
= |
|
|
|
|
|
|
r r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2b |
|
|
|
|
= 0.271 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
V − b |
|
RTV |
|
|
|
|
|
|
|
2Vr |
− 1 |
|
|
|
|
|
|
4e |
2 |
b |
2 |
|
|
|
|
|
|
4Rb |
|
|
|
e |
2 |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
Бертло (1900) |
|
|
|
|
|
|
|
|
RT |
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
8Tr |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
3 |
|
|
|||||||||||||
|
|
|
|
|
|
p = |
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
p |
|
= |
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
1 |
2aR |
1 |
2 |
|
2 a |
|
1 |
|
|
|
|
|
= 0.375 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3b |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
V − b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
TV 2 |
|
|
|
|
r |
|
|
3V |
|
T V |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3b |
3 |
|
3 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
r r |
|
|
12 |
|
|
|
|
3bR |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
p = ( |
|
|
|
|
|
) |
|
|
|
|
|
|
( |
|
|
|
|
|
) |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Битти-Бриджмена (1927) |
|
|
1− γ |
|
RT |
|
|
|
V + β − α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V 2 |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
где α = a |
|
|
|
1 |
+ |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
β = b |
|
|
1 |
− |
b |
|
, |
|
γ= |
|
|
|
c0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
V |
|
VT |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Вириальное (1901) |
|
RT |
|
|
|
B2 |
|
|
|
|
B3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
(Камерлинг-Оннес) |
p = |
|
|
|
|
1+ |
|
|
|
|
|
|
+ |
|
|
|
+ |
... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
V |
|
|
V |
|
V |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
термодинамики химической Основы .1 а в а л Г
19
20 |
Г л а в а 1. Основы химической термодинамики |
(1.5.а)
(1.5.б)
(1.6)
Наиболее известным уравнением, описывающим одновременно свойства и газа, и жидкости, является уравнение Ван-дер-Ваальса:
|
|
p = |
|
|
RT |
|
|
− |
a |
|
|
|
|
|
|
Vm − b |
|
|
|
||||||||
|
|
|
|
Vm2 |
|
|
|||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
RT |
|
2 |
a |
ab |
|
||||||
Vm |
− b + |
|
Vm + |
|
Vm − |
|
= 0 |
||||||
p |
|
p |
|||||||||||
|
|
|
|
|
p |
|
|||||||
Уравнение (1.5) – кубическое и, следовательно, имеет или три действительных корня, или один действительный и два мнимых. При температурах выше критической уравнение (1.5) имеет один действительный корень, и по мере повышения температуры кривые, вычисленные по уравнению Ван-дер-Ваальса, приближаются к гиперболам, соответствующим уравнению состояния идеального газа (рис. 1.3.б). При температурах ниже критической расчет по уравнению Ван-дер-Ваальса дает волнообразные кривые с тремя действительными корнями, из которых только два (точки 1 и 2) физически осуществимы. Третий корень (точка 3) физически нереален, поскольку находится на участке
кривой, соответствующем условию |
|
∂p |
> 0 . Согласно построению |
|
|
|
|
||
|
||||
|
|
∂V T |
|
|
Максвелла для того, чтобы расчетная кривая соответствовала экспериментальной равновесной изотерме, нужно вместо волнообразной кривой провести горизонтальную прямую так, чтобы отсекаемые ею площади под кривой были равны.
В критической точке изотермы реальных газов имеют точку перегиба, координаты которой можно определить из условий
|
∂p |
|
= 0, |
|
|
|
|
|
|
∂V |
|
|||
|
T =Tc |
|
||
|
|
|
|
|
|
∂ 2 p |
|
|
|
|
= 0. |
|||
|
|
|
|
|
|
2 |
|||
|
∂V |
|
|
|
|
|
T =T |
c |
|
|
|
|
|
|
Эти уравнения позволяют связать индивидуальные постоянные уравнения с критическими параметрами газа (см. пример 1-3 и таблицу П-1 в Приложении).
Вводя безразмерные приведенные переменные: давление pr = p/pc, объем Vr = V/Vc и температуру Tr = T/Tc, можно получить приведенное уравнение состояния реального газа, которое не содержит в явном виде индивидуальных постоянных (см. пример 1-3 и таблицу П-1).
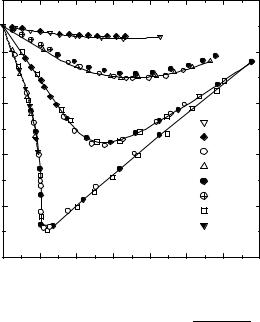
Г л а в а 1. Основы химической термодинамики |
21 |
Состояния разных веществ, имеющие одинаковые значения приведенных переменных, называют соответственными. Согласно закону соответственных состояний, если для рассматриваемых газов значения двух приведенных переменных одинаковы, должны совпадать и значения третьей приведенной переменной. Таким образом, уравнения состояния различных веществ, записанные в приведенных переменных, должны совпадать. Это утверждение эквивалентно постулату о существовании общего универсального приведенного уравнения состояния:
|
|
|
|
|
|
|
|
F(pr, Vr, Tr) = 0. |
|
|
|
|
|
(1.7) |
|
||
|
Поскольку |
это |
уравнение |
|
1.1 |
|
|
|
|
|
|
|
|||||
не |
содержит |
в |
явном |
|
виде |
|
|
|
|
Tr |
= 2.0 |
|
|
|
|||
индивидуальных |
постоянных, |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||
оно должно быть применимо к |
|
0.9 |
|
|
Tr |
= 1.5 |
|
|
|
||||||||
любому газу. Закон соответст- |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|||||||||
венных |
состояний |
является |
pV/RT |
|
|
|
|
|
|
|
|
||||||
общим утверждением, не свя- |
0.7 |
|
|
|
|
|
|
|
|||||||||
занным с |
конкретным |
видом |
|
|
|
T = 1.2 |
|
CH4 |
|
||||||||
уравнения состояния. На прак- |
|
|
|
r |
|
|
N2 |
|
|||||||||
Z = |
|
|
|
|
|
|
|
||||||||||
тике |
закон |
соответственных |
0.5 |
|
|
|
|
|
C2H4 |
|
|||||||
состояний |
приближенно |
вы- |
|
|
|
|
|
|
|
C2H6 |
|
||||||
|
|
|
Tr = 1.0 |
|
|
|
C3H8 |
|
|||||||||
полняется |
для |
однотипных |
|
|
|
|
|
|
|
||||||||
веществ, что позволяет, напри- |
|
0.3 |
|
|
|
|
|
H2O |
|
||||||||
|
|
|
|
|
|
C4H10 |
|
||||||||||
мер, использовать для реаль- |
|
|
|
|
|
|
|
CO2 |
|
||||||||
ных газов обобщенные диа- |
|
0.1 |
|
|
|
|
|
|
|
||||||||
граммы сжимаемости (рис. 1.4). |
|
1.0 |
2.0 |
3.0 |
4.0 |
5.0 |
6.0 |
7.0 |
|||||||||
|
|
|
|
|
|
|
|
|
|
0.0 |
|||||||
|
С высокой точностью по- |
|
|
|
|
|
pr |
|
|
|
|||||||
ведение любого реального газа |
Зависимость фактора сжимаемости |
|
Рис. 1.4 |
|
|||||||||||||
можно описать с помощью ви- |
|
|
|||||||||||||||
риального |
уравнения состоя- |
|
некоторых газов от приведенного |
|
|
|
|||||||||||
|
давления при разных приведенных |
|
|
|
|||||||||||||
ния – бесконечного ряда по |
|
|
|
|
|||||||||||||
|
|
температурах |
|
|
|
|
|||||||||||
степеням обратного объема: |
|
|
|
|
|
|
|
|
|
||||||||
|
|
RT |
|
|
B |
2 |
|
|
|
B |
3 |
|
|
|
||
p = |
|
|
1 |
+ |
|
|
|
+ |
|
|
+... |
(1.8.а) |
||||
|
|
|
|
|
|
|
|
2 |
||||||||
|
|
|
|
|
|
Vm |
|
|
|
|
|
|||||
|
|
Vm |
|
Vm |
|
|
|
|||||||||
или давления |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
RT |
|
|
|
' |
|
|
|
' |
|
2 |
|
|
|||
p = |
|
(1+ B2 p |
+ B3 p |
|
+...), |
(1.8.б) |
||||||||||
Vm |
|
|||||||||||||||
где Bi, Bi' – i-ые вириальные коэффициенты, которые зависят от природы газа и от температуры. Первый вириальный коэффициент равен 1. Так как в большинстве случаев B2/V >> B3 /V 2 >> ..., при описании экспериментальных данных ограничиваются вторым вириальным коэффициентом. При низких температурах B2 < 0, с ростом температуры его
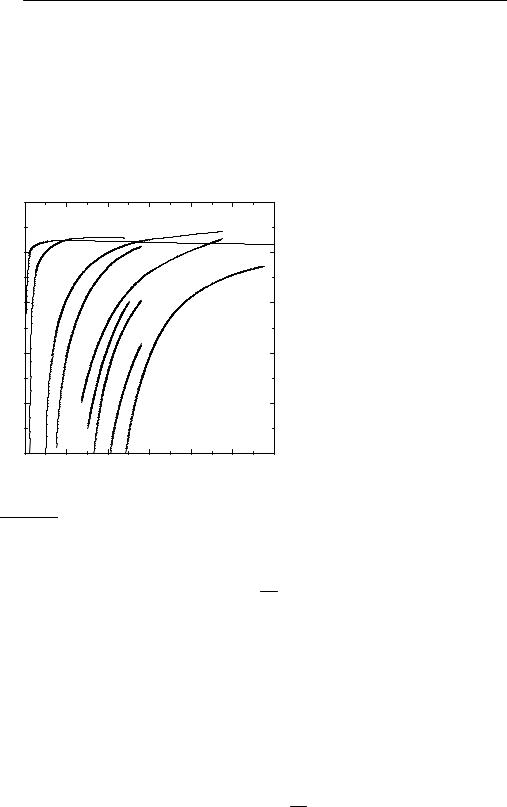
22 |
|
|
|
Г л а в а 1. Основы химической термодинамики |
|
|
|
|
|||||||
|
|
значение проходит через ноль, затем становится положительным, дос- |
|||||||||||||
|
|
тигает максимума и далее очень медленно убывает. При высоких тем- |
|||||||||||||
|
|
пературах B2 и все последующие вириальные коэффициенты стремятся |
|||||||||||||
|
|
к нулю (рис. 1.5). Температура, при которой B2 = 0, называется темпе- |
|||||||||||||
|
|
ратурой Бойля. При этой температуре фактор сжимаемости реального |
|||||||||||||
|
|
газа близок к 1 при любых давлениях. Значения вторых вириальных ко- |
|||||||||||||
|
|
эффициентов некоторых газов при разных температурах приведены в |
|||||||||||||
|
|
приложении (табл. П-3). |
|
|
|
Термическое уравнение со- |
|||||||||
|
50 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
стояния |
можно |
|
определить |
||||
|
He |
|
|
|
|
|
|
|
экспериментально, |
изучая, на- |
|||||
|
|
|
|
|
|
|
|
пример, |
зависимость |
объема |
|||||
|
0 |
|
|
|
|
|
|
|
|||||||
|
|
|
CH4 |
Xe |
|
|
|
фазы от температуры и давле- |
|||||||
|
H2 |
Ar |
|
H2O |
|
ния. При этом получают вели- |
|||||||||
|
|
|
|
|
|
|
|||||||||
−1 |
|
|
|
NH3 |
|
|
чины, |
называемые |
|
термиче- |
|||||
-50 |
|
|
|
|
|
|
|
||||||||
3 моль |
|
|
|
|
|
|
|
скими коэффициентами: |
|
||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
C H |
|
|
|
|
(1.9.а) |
|
∂V |
|
|
= |
−βV0 , |
|
, см |
|
|
|
3 8 |
|
|
|
|
|
|
|
||||
-100 |
|
|
|
|
|
|
|
|
|
∂p |
|
T |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
где β – изотермический коэф- |
||||||
|
|
|
|
|
|
|
|
|
|||||||
|
-150 |
|
|
|
|
|
|
|
фициент сжимаемости, |
|
|
||||
|
-2000 |
C2H6 |
|
|
|
|
|
(1.9.б) |
|
(∂∂VT )p |
= αV0 , |
||||
|
200 |
400 |
600 |
800 |
1000 |
1200 |
где α – изобарный коэффици- |
||||||||
|
|
|
|
T, K |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
ент расширения, V0 – объем |
|||||||
|
|
|
Зависимость второго вириального |
|
|||||||||||
|
Рис. 1.5 |
|
|
при T = 0 K. |
|
|
|
|
|
||||||
|
|
|
коэффициента некоторых газов |
|
К термическим коэффици- |
||||||||||
|
|
|
|
от температуры |
|
|
ентам относится также частная |
||||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
производная |
|
|
|
|
|
|
|
(1.9.в) |
|
|
|
|
∂p |
= γp , |
|
|
|
|
|
|
||
|
|
|
|
|
|
∂T |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
где γ – изохорный коэффициент давления. |
|
|
|
|
|
|
|||||||
|
|
|
Последнюю величину для конденсированной фазы нельзя измерить |
||||||||||||
|
|
экспериментально, так как невозможно нагреть тело, чтобы не изме- |
|||||||||||||
|
|
нился его объем или объем оболочки, в которую оно помещено. Коэф- |
|||||||||||||
|
|
фициент γ можно рассчитать, используя цепочечное соотношение Эй- |
|||||||||||||
|
|
лера (см. Приложение IV): |
|
|
|
|
|
|
|
|
|
||||
(1.10)
откуда
(1.11)
|
∂p |
|
∂V |
|
∂T |
= −1, |
|
|
|
|
|
|
|
|
|
|
|||||||
|
∂V T |
∂T p |
∂p V |
|
|||
γ = βαp .

Г л а в а 1. Основы химической термодинамики |
23 |
Если известны термические коэффициенты, то уравнение состояния конденсированной фазы можно получить, интегрируя дифференциальное уравнение
|
∂V |
|
∂V |
dT . |
(1.12) |
dV = |
|
dp + |
|
||
|
∂p T |
|
∂T p |
|
|
Уравнение состояния идеального газа и вириальное уравнение состояния реального газа можно вывести методами статистической термодинамики (см. § 16).
ПРИМЕРЫ
Пример 1-1. Докажите, что при больших объемах уравнение Ван- дер-Ваальса переходит в уравнение идеального газа.
Решение. Уравнение Ван-дер-Ваальса для 1 моля:
p = |
RT |
− |
a |
. |
V − b |
|
|||
|
V 2 |
|||
При больших объемах вторым слагаемым в правой части можно пренебречь: a/V 2 → 0. В знаменателе первого слагаемого можно пренебречь постоянной b: V – b → V. В пределе получаем уравнение состояния идеального газа:
V →∞ |
RT |
|
p → |
|
. |
V |
||
Пример 1-2. Найдите вириальные коэффициенты Bi для газа, подчиняющегося уравнению Ван-дер-Ваальса.
Решение. В уравнении Ван-дер-Ваальса выделим сомножитель RT/V:
|
RT |
|
a |
|
RT |
|
|
|
1 |
|
|
a |
|
p = |
− |
= |
|
|
|
|
− |
. |
|||||
|
|
|
|
|
|
|
|
||||||
|
V − b |
|
V 2 |
|
V |
|
1 |
− |
b |
|
RTV |
||
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
Если разложить первое слагаемое в скобке в ряд по степеням b/V, получим:
|
RT |
|
b n |
|
a |
|
|||
p = |
|
|
|
|
|
|
− |
|
. |
|
∑ |
|
|||||||
|
V |
|
|
|
|
||||
|
n=0 |
V |
|
RTV |
|||||
Из этого разложения следует, что второй вириальный коэффициент газа Ван-дер-Ваальса зависит от температуры:
B2 = b − RTa ,
а остальные постоянны: Bn =bn−1 .

24 |
Г л а в а 1. Основы химической термодинамики |
Пример 1-3. Найдите критические параметры и приведенное уравнение состояния для газа Дитеричи.
Решение. Запишем уравнение Дитеричи в виде:
|
|
a |
|
p(V − b) = RT exp |
− |
|
|
|
|||
|
|
RTV |
|
и продифференцируем левую и правую части этого уравнения два раза по объему при постоянной температуре:
|
∂ 2 p |
|
|
∂p |
|
|
|
a |
|
|
|
a 2 |
|
|
|
2a |
|
|
|||||
|
|
|
|
(V − b) + 2 |
|
|
|
= RT exp |
|
− |
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
2 |
|
|
|
2 |
|
2 |
|
4 |
|
3 |
||||||||||||
|
∂V |
|
|
|
|
|
|
|
R |
T |
V |
|
RTV |
|
|||||||||
|
|
T |
|
|
∂V T |
|
|
|
RTV |
|
|
|
|
|
|
|
|||||||
и учтем, что в критической точке первая и вторая производные равны 0:
|
|
a 2 |
2a |
|
|
|
|
|
|
− |
|
|
= 0 , |
R |
2 |
2 4 |
RTV |
3 |
||
|
T V |
|
|
|||
откуда находим:
TcVc = 2aR .
Если продифференцировать обе части уравнения состояния по объему один раз с учетом равенства нулю первой производной, то можно найти второе соотношение между критическими объемом и температурой:
|
∂p |
|
a |
|
|
|
a |
|
ap(V − b) |
|
|||
p + |
|
|
(V − b) = |
|
|
RT exp |
− |
|
|
= |
|
|
, |
|
RTV |
2 |
|
RTV |
2 |
||||||||
|
∂V |
T |
|
|
|
RTV |
|
|
|
||||
откуда
RTcVc 2 = a(Vc − b) .
Подставляя сюда первое найденное соотношение для критических параметров, получим:
Vc = 2b, |
Тc = |
a |
. |
|
|||
|
|
4Rb |
|
И, наконец, подставляя эти параметры в уравнение состояния, находим критическое давление:
pc = |
a |
. |
|
4b2e2 |
|||
|
|

Г л а в а 1. Основы химической термодинамики |
25 |
Для вывода приведенного уравнения состояния подставим в уравнение Дитеричи приведенные переменные:
p = pr |
a |
, |
V = 2bVr , |
T = Tr |
a |
. |
4b2e2 |
|
|||||
|
|
|
|
4Rb |
||
В результате получаем приведенное уравнение Дитеричи, не содержащее индивидуальных параметров:
|
|
|
pr (2Vr |
− 1) = Tr exp 2 − |
2 |
|
. |
|
|
|
|
|
|||||
|
|
|
|
|
|
VrTr |
||
Пример 1-4. Выведите уравнение состояния кристаллического |
||||||||
вещества, |
если известно, |
что термические |
коэффициенты равны |
|||||
α = |
a + cp |
и β = |
b − cT |
, где a, b, c – некоторые постоянные величины. |
||||
V0 |
|
|||||||
|
|
V0 |
|
|
|
|
||
Решение. Запишем уравнение состояния данной фазы в дифференциальной форме:
dV = αV0dT − βV0dp = a + cp V0dT − b − cT V0dp = V0 V0
= (a + cp)dT + (cT − b)dp .
Чтобы проинтегрировать это выражение, надо выяснить, является ли dV полным дифференциалом, т.е. выполняется ли равенство смешанных производных:
∂(cT − b) |
= |
∂(a + cp) |
с = с. |
∂T |
|
∂p |
|
Далее проводим интегрирование по температуре с постоянной интегрирования ϕ, зависящей от давления:
V = aT + cTp + ϕ(p).
Дифференцируя полученное уравнение по p и учитывая выражение для dV, получаем:
|
∂V |
|
∂ϕ( p) |
|
|
∂ϕ( p) |
|
||
|
|
= cT − b = cT + |
∂p |
|
−b = |
∂p |
|
||
|
∂p T |
|
T |
|
|
T |
|
||
ϕ(p) = –bp + const.
Следовательно,
V = aT + cTp – bp + const.
При T, p = 0, V0 = const.
Окончательно,
V = V0 + aT + cTp – bp.

26 |
Г л а в а 1. Основы химической термодинамики |
ЗАДАЧИ
1-1. Приведите пример термодинамического процесса, который может совершаться как обратимо, так и необратимо. Назовите для этого процесса по одной функции состояния и перехода.
1-2. Приведите пример обратимого, но неравновесного термодинамического процесса.
1-3. Приведите примеры систем со временем релаксации порядка: а) секунд; б) часов;
в) десятилетий.
1-4. Изменение теплоты в зависимости от температуры и объема в некоторой системе описывается уравнением:
δQ = C dT + (RT /V )dV
(C и R – постоянные). Является ли теплота функцией состояния в данном случае? Ответ обоснуйте.
1-5. Зависимость теплоты некоторого процесса от температуры и давления описывается выражением:
δQ = (RT p)dp − RdT .
p)dp − RdT .
Является ли теплота функцией состояния в данном случае?
1-6. Относительная влажность воздуха в комнате объемом 500 м3 при 298 К равна 87%. Давление насыщенного пара воды при этой температуре равно 0.0313 атм. Рассчитайте массу воды, находящейся в воздухе в виде пара.
1-7. Давление насыщенного пара ртути при 300 К равно 0.002 Торр. Плотность воздуха при этой температуре равна 1.18 г л–1. Рассчитайте:
а) концентрацию паров ртути в воздухе в моль л–1; б) весовое содержание ртути в воздухе в миллионных долях (млн–1).
1-8. Докажите, что при больших объемах уравнение Дитеричи переходит в уравнение идеального газа.
1-9. Найдите частные производные |
∂p |
|
и |
∂p |
|
|
для: |
||||
|
|
||||||||||
|
|
|
|
∂T |
V |
∂V |
|
T |
|||
а) идеального газа; |
|
|
|
|
|
|
|
|
|
|
|
б) газа Ван-дер-Ваальса; |
|
|
|
|
|
|
|
|
|||
в) газа, подчиняющегося уравнению Дитеричи. |
|
|
|||||||||
Докажите, что |
∂ 2 p |
= |
∂ 2 p |
. |
|
|
|
|
|
|
|
∂V ∂T |
∂T ∂V |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
