
Lektsia_26
.pdf
Лекція 26. Інтеграл від функції комплексної змінної. Теорема Коші. Інтеграл Коші. Похідна будь-якого порядку від аналітичної функції.
Інтеграл від функції комплексної змінної.
|
|
|
|
z |
z |
k−1 |
ζk |
zk |
|
|
|
|
||
z2 |
|
|
|
|
|
|
|
|
|
z1 |
|
|
zn−1 |
z =b |
|
|
|
n |
|
|
|
|
|
z0=a
0
Розглянемо на комплексній площині кусковогладку криву . Нехай на цій кривій визначена функція
( ) комплексної змінної . Розіб’ємо криву на частинних дуг точками
Покладемо
і складемо суму
|
∑ ( ) |
(1) |
де – довільно взята точка |
-ої частини дуги |
|
. |
|
|
Нехай |
| |
| |
|
. Якщо при |
|
інтегральна сума (1) має границю, яка не залежить від способу розбиття кривої на частинні дуги і від вибору точок на них, то ця границя називається інтегралом від функції ( ) по кривій
∑ |
( |
) |
|
∫ |
( ) |
(2) |
Нехай ( ) |
( |
|
) |
( |
), |
|
, |
|
|
|
|
, |
, |
, |
|
( |
) |
, |
( |
) |
|
|
|
|
|
Тоді інтегральну суму (1) можна записати в наступному вигляді:
∑ ( )
∑( ( ) ( ))( |
) |
∑( )
∑( )
Дійсна і уявна частини суми (1) є інтегральними
сумами криволінійних інтегралів другого роду
∫ ∫
Питання про існування інтегралу (2) зводяться до питання існування звичайних криволінійних інтегралів від функції дійсних змінних. Для існування цих інтегралів достатньо, щоб функції ( ) і ( ) були кусково-неперервними.
Отже
∫ ( ) ∫ |
∫ |
(3) |
|
|
Властивості інтегралів по комплексній змінній.
1. |
∫ ( ) |
∫ ( ) |
|
|
2. |
∫ ( ) |
∫ ( ) |
∫ ( ) |
|
|
|
3. Якщо – комплексна змінна, тоді
|
|
∫ ( ) |
∫ ( ) |
|
4. |
∫ ( ) |
( ) |
∫ ( ) |
∫ ( ) |
|
|
|
|
|
5. Нехай |
| |
( )| |
|
|
|
, – довжина кривої . |
|||
Тоді |
|
|
|
|
|
|∫ ( ) |
| ∫| ( )|| | |
∫| | |
|
Теорема Коші. Інтеграл Коші.
При інтегруванні по замкнутому контурі додатнім напрямком будемо вважати напрямок проти годинникової стрілки.
Інтегрування в додатному напрямку будемо позначати символом:
∫ ( ) |
∫ ( ) |
Увід’ємному напрямку
∫( )
Теорема 1. (Перше формулювання теореми Коші). Нехай в однозв’язній області задано однозначну аналітичну функцію ( ). Тоді інтеграл від цієї функції по будь-якому замкненому контуру області дорівнює нулю
∫ ( )
Згідно з формулою (3), маємо

∫ ( ) ∫ |
∫ |
(4) |
|
|
Оскільки функція ( ) – аналітична в області , то функції ( ) в області мають неперервні
частинні похідні першого порядку і задовольняють умовам Коші-Рімана.
Тому до криволінійних інтегралів рівності (1) можна застосувати формулу Гріна.
∫ |
( |
|
|
|
) |
|
|
∫ |
( |
|
|
|
) |
|
|
Теорема 2. (друге формулювання теореми Коші).
Якщо функція ( ) є аналітичною функцією в однозв’язній області , обмеженій кусково-гладким
контуром , і неперервна в замкнутій області , то
інтеграл від функції ( |
) по границі |
області |
дорівнює нулю: |
|
|
∫ |
( ) |
|
Зауваження. Теорему 2 можна узагальнити на випадок багатозв’язної області. В цьому випадку повна границя області складається із декількох замкнутих
контурів – зовнішнього |
і внутрішніх |
. |
Зорієнтуємо повну границю області |
наступним |
|
чином. Додатнім напрямком обходу границі |
||
багатозв’язної області будемо називати такий |
||
напрямок руху, при якому область весь час |
||
залишається зліва. При цьому зовнішній контур |
||
обходиться в додатному напрямі, а внутрішній – в |
||
від’ємному. |
|
|
Теорема 3. Нехай ( |
) є аналітичною функцією в |
|
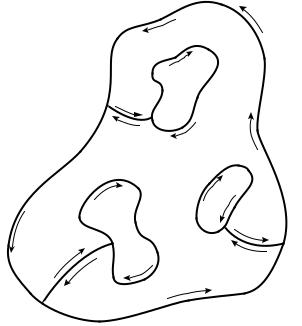
багатозв’язній області , обмеженій ззовні контуром
, а зсередини контурами |
|
і нехай ( ) – |
неперервна в замкнутій області |
|
. Тоді |
|
||
∫ ( ) |
|
|
γ1 |
Γ1 |
|
Γ2 |
||
|
||
Γn−1 |
|
|
γn−1 |
γ2 |
|
|
||
|
Γ0 |
|
Рис. 1 |
|
|
Проведемо гладкі криві |
, які |
|
з’єднують контур з контурами |
і т.д. Тоді |
|
область, обмежена кривими |
і кривими |
, які проходять двічі в протилежних напрямках, є однозв’язною.
За теоремою 2 інтеграл по границі цієї області дорівнює нулю. Але інтеграли по допоміжних кривих
проходять двічі в протилежних напрямках, тому взаємно знищуються.
Тому має місце рівність
∫ ( ) |
∫ ( ) |
∫ ( ) |

Інтеграл Коші |
|
|
|
|
|
|
|
|
Нехай функція |
( |
) є аналітичною в однозв’язній |
||||||
області |
, обмеженій контуром |
. Тоді для довільної |
||||||
точки |
має місце інтегральна формула Коші |
|||||||
|
( |
) |
|
|
∫ |
|
( ) |
|
|
|
|
|
|
|
|||
Візьмемо довільну внутрішню точку і побудуємо замкнутий контур , який повністю лежить
ві містить точку . Розглянемо допоміжну функцію
( ) |
( ) |
|
|
|
|
|
|
|
Функція ( ) є аналітичною всюди в області за |
||
винятком точки . |
|
|
Γ
γ
γ1
ρ
z0
Рис. 2
Якщо в області |
|
візьмемо такий замкнутий контур |
|||||||
, який лежить всередині , щоб точка |
попала |
||||||||
всередину області, яка обмежена контуром . |
|||||||||
Тоді функція |
( |
) буде аналітичною в двохзв’язній |
|||||||
області , яка знаходиться між контурами |
і . |
||||||||
Згідно теореми Коші інтеграл від функції |
( |
) по |
|||||||
кривій |
дорівнює нулю: |
|
|
||||||
|
∫ |
|
( ) |
|
∫ |
( ) |
|
|
|
|
|
|
|
|
|
|
|||
Поміняємо напрямок інтегрування в другому інтегралі:
∫ |
( ) |
∫ |
( ) |
|
|
(6) |
|||
|
|
|
||
В якості контура інтегрування виберемо коло радіуса з центром в точці .
Покладемо
Тоді
