
Lektsia_7
.pdf
Лекція 7. Криволінійні інтеграли другого роду. Формула Гріна. Умови незалежності криволінійного інтегралу від шляху інтегрування.
|
|
|
Рис. 1 |
|
Нехай у площині |
задано гладку криву |
і на цій кривій задана |
||
функція |
. Розіб’ємо криву |
точками |
|
|
|
|
|
на довільних частин, на кожній |
|
частині дуги |
|
виберемо точку |
|
|
|
∑ |
∑ |
|
(1) |
де |
– проекція дуги |
на вісь |
. |
|
Нехай |
. Якщо при |
інтегральна сума (1) |
||
має скінченну границю, то цю границю називають криволінійним |
||||
інтегралом другого роду від функції |
|
по координаті вздовж |
||
кривої |
: |
|
|
|
|
∫ |
|
∫ |
|
Аналогічно одержуємо криволінійний інтеграл другого роду від функціі по координаті :
∫ ∑
де |
– проекція дуги |
на вісь |
. |
|
|
|
Якщо вздовж кривої |
визначені дві функції |
, |
||
|
|
і існують інтеграли |
|
|
|
|
∫ |
∫ |
|
∫ |
∫ |
то їх суму називають криволінійним інтегралом загального вигляду:
∫
Зауваження. На відміну від криволінійного інтеграла першого роду криволінійний інтеграл другого роду залежить від напряму шляху інтегрування і при зміні цього напряму змінює свій знак.
Напрямок шляху |
вздовж якого інтегруємо не грає ролі в випадку |
|||
інтегралу першого роду, так як довжина |
дуги |
̆ від цього |
||
напрямку не залежить. |
|
|
||
Для інтегралу другого роду : проекції |
і |
дуги ̆ на |
||
відповідно осі |
і |
суттєво залежать від напрямку дуги , і інтеграл |
||
міняє знак при зміні цього напряму на обернений. |
|
|||
Таким чином, |
|
|
|
|
∫ |
|
|
∫ |
|
Вирахування криволінійного інтегралу другого роду: Нехай крива задана параметричним рівнянням
.
Функції |
, |
– неперервні на |
. Існують неперервні похідні |
|
. При зміні |
крива описується в напрямку від до |
|
. |
|
|
|
За означенням:
∫ |
∑ |
(2) |
За формулою Лагранжа:
Виберемо точку |
так, щоб |
, тоді (2): |
∑ ( |
) |
(3) |
|
|
Це інтегральна сума для функції ( |
) |
на проміжку |
, |
тому |
|
|
|
∫ |
∫ ( |
) |
Аналогічно
∫ |
∫ ( |
) |
Якщо крива |
задана рівнянням |
, тоді (4) |
∫ |
∫[ ( |
) ( |
) ] |
Тоді:
Якщо крива |
задана параметричним рівнянням |
|
. |
∫
(4)
∫[ ( |
) |
( |
) |
] |
Зведення криволінійного інтегралу другого роду до криволінійного інтегралу першого роду
|
|
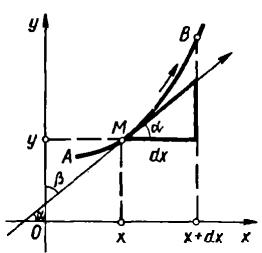
Рис. 2 |
Позначимо через |
і кути, які утворює з осями координат дотична до |
|
кривої |
у точці |
. За додатній напрям дотичної беремо той, який |
відповідає напряму руху точки по кривій від до Враховуючи геометричний зміст диференціала функції та диференціала дуги, маємо
.
Тоді , одержуємо формулу, яка виражає криволінійни інтеграл другого роду через криволінійний інтеграл першого роду:
∫ |
∫ |
Часто доводиться розглядати криволінійні інтеграли по замкненому контуру, тобто контуру інтегрування, в якому початкова і кінцева точки збігаються.
Якщо контур замкнений, то додатним вважається обхід проти стрілки годинника.
Криволінійний інтеграл по додатньо орієнтованому контуру позначають так:

Формула Гріна.
Теорема. Нехай – деяка правильна область, обмежена замкненим
контуром . Функції |
, |
– неперервні разом із своїми |
|
частинними похідними |
і |
|
в цій області. Тоді |
|
|||
( )
