
Lektsia_28
.pdfЛекція 28. Ряд Лорана. Ізольовані особливі точки функції комплексної змінної.
Розглянемо ряд вигляду
∑ |
( |
) |
(1) |
де – фіксована точка комплексної площини, |
– |
||
деякі комплексні числа. |
|
|
|
Ряд (1) називається рядом Лорана. Причому, сукупність членів цього ряду з невід’ємними степенями ( ) називається правильною частиною ряду Лорана, а з від’ємними – його головною частиною.
Подамо ряд (1) в вигляді
|
( ) |
|
( |
) |
|
|
|
∑ |
∑ |
∑ ( ) |
|||||
|
|
|
|||||
Область збіжності ряду
∑ ( )

є круг з центром в точці і радіуса . Всередині круга збіжності цей ряд збігається до деякої аналітичної функції комплексної змінної
( ) ∑ ( ) | | |
(2) |
Для визначення області збіжності ряду
∑ |
|
(3) |
( ) |
зробимо заміну змінної
Тоді (3)
∑ |
(4) |
Тобто він представляє собою звичайний степеневий ряд, який збігається до деякої аналітичної функції ( ) комплексної змінної .
Позначимо радіус збіжності ряду (4) через . Тоді
( ) |
|
∑ |
|
|
|
| | |
|
|
|
||
|
|
|
|
|
|||||||
Перейдемо до змінної : |
|
|
|
|
|||||||
|
|
( ( |
)) |
|
( ) |
|
|
|
|||
|
|
( ) |
|
|
|
|
|
|
|
|
|
|
|
∑ ( |
) |
|
|
|
|||||
|
|
|
|
|
|
|
|
||||
| |
|
|
| |
|
|
| |
| |
|
|
|
|
|
|
|
|
|
|
|
|||||
Якщо |
, то існує область збіжності, де |
||||||||||
збігаються два ряди (2) і (3). Ця область представляє кільце
| |
в якому ряд (1) збігається до аналітичної функції
( ) ( ) ( ) ∑ ( )
| |
Отже ряд Лорана (1) збігається всередині свого круга збіжності до деякої функції ( ), аналітичної в даному кільці.
Якщо |
|
|
ряди (2) і (3) загальної області не |
|||||
мають. |
|
|
|
|
|
|
|
|
Теорема.Функція |
( |
), аналітична в круговому кільці |
||||||
| |
| |
, однозначно подається в цьому |
||||||
кільці збіжним рядом Лорана (1) |
|
|||||||
( ) |
∑ |
|
( |
|
) |
(5) |
||
де |
|
|
|
|
|
|
|
|
|
|
∫ |
|
( ) |
|
|
|
( ) |
|
|
|
|
|
|
|
||
|
|
( |
) |
|
|
|
||
– коло радіуса |
| |
| |
, |
. |
||||
Ізольовані особливі точки однозначної аналітичної функції.
Означення.Точка називається ізольованою
особливою точкою функції |
( ), якщо ( ) – |
||
однозначна і аналітична в круговому кільці |
|||
| |
| |
, а точка |
є особливою точкою |
функції |
( ). В самій точці |
функція ( ) може бути |
|
не визначена. |
|
|
|
Означення.Якщо існує скінченна границя |
|||
|
|
( ) |
, |
то ізольовану особливу точку |
|
називають усувною. |
|||||
Означення.Якщо |
|
( |
) |
, тоді ізольована |
|||
особлива точка |
називається полюсом. |
|
|||||
Нехай |
- полюс функції |
( |
) і існує не рівна нулю |
||||
кінцева границя |
|
|
|
|
|
|
|
|
|
( |
) |
( |
) |
|
|
Тоді точка |
– полюс |
-го порядку функції ( ). |
|
||||
Означення.Якщо |
|
( ) не існує (і не дорівнює |
), |
||||
тоді – суттєво особливо точка. |
|
|
|||||
Теорема 2.Ізольована особлива точка |
функції ( |
) є |
|||||
усувною особливою точкою тоді і тільки тоді, якщо |
|
||||||
розклад в функції |
( ) в околі точки |
не містить |
|
||||
головної частини, тобто має вигляд |
|
|
|||||
( ) ∑ ( )
Теорема3.Ізольована особлива точка функції ( ) є полюсом в тому випадку тоді і тільки тоді, якщо головна частина розкладу в ряд Лорана функції ( ) в околі точки містить скінченну кількість відмінних від нуля значень

( ) ∑ ( )
Теорема4.Ізольована особлива точка є суттєво особливою тоді і тільки тоді, коли головна частина розкладу в ряд Лорана функції ( ) в околі цієї точки містить нескінченну кількість відмінних від нуля членів.
( ) ∑ ( )
Приклад 1. Функція ( ) |
|
|
|
в точці |
не |
|
|||||
|
|
|
|
||||||||
визначена. В точці |
функція не аналітична. |
|
|||||||||
|
|
|
|
|
|
( ) |
|
|
|
||
|
|
|
|
|
|
( |
) |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
( )
Отже – усувна точка
Функція

( ) {
є неперервною і аналітичною при .
Приклад 2.
Функція
в точках |
|
не визначена і не аналітична. |
|
|
|
||||||||||||||
|
|
|
|
|
( |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
тобто точка |
|
|
– полюс кратності . |
|
|
|
|
|
|
|
|||||||||
|
|
|
( |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
точка |
– полюс кратності . |
|
|
|
|
|
|
|
|
|
|
|
|||||||
Приклад 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Розкласти в ряд Лорана функцію |
( ) |
|
|
|
|
|
|
|
в |
||||||||||
|
( )( |
) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
а) |
* | | |
|
+, при |
|
|
|
|
|
|
|
|
|
|
|
|||||
а) |
* | | |
+ |
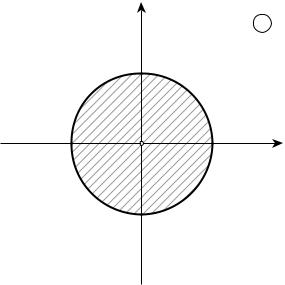
y
z
z0=0
1 x
Перетворимо |
( ) наступним чином: |
|||||||||||||
( ) |
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
( )( |
) |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Використовуючи формулу |
|
|||||||||||
|
|
|
|
| |
| |
(9) |
||||||
|
|
|
|
|||||||||
одержуємо |
|
|
||||||||||
|
|
|
|
|
| |
|
| |
(10) |
||||
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
, тобто при | | |
|
|
Цей ряд збігається для | |
|
| |
. |
|||||||||
|
||||||||||||
( ) |
( |
|
|
) |
|
|
( |
) |
( |
|
) |
( |
) |
( |
|
|
) |
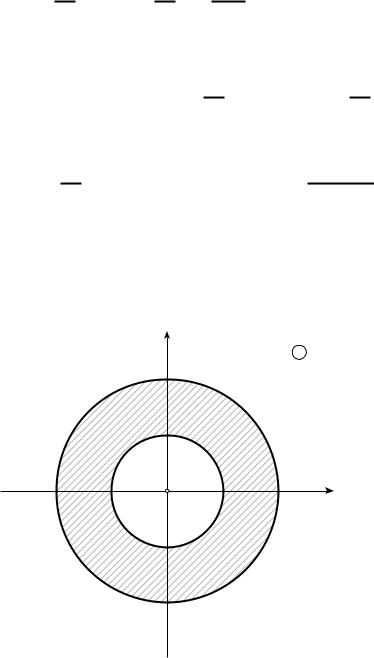
б) |
* |
|
| |
| |
+ ,при |
|
y |
|
|
z |
|
|
|
|
|
|
|
|
z0=0 |
1 |
2 |
x |
|
|
|
|
|||
Ряд (10) збігається при | |
| |
|
|
збігається в цьому |
|
кільці. Ряд (9) для функції |
|
|
|
||
|
розбігається для | |
| |
. Тому подамо функцію |
|
|||
( ) в такому вигляді |
|
|
|
( )
Використовуючи формулу (9), одержуємо
(11)
Цей ряд збігається для | |
|
| |
|
, тобто при | | |
. |
|||||||||||
|
||||||||||||||||
( ) |
|
( |
|
|
|
) |
|
|
( |
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
||||||||||
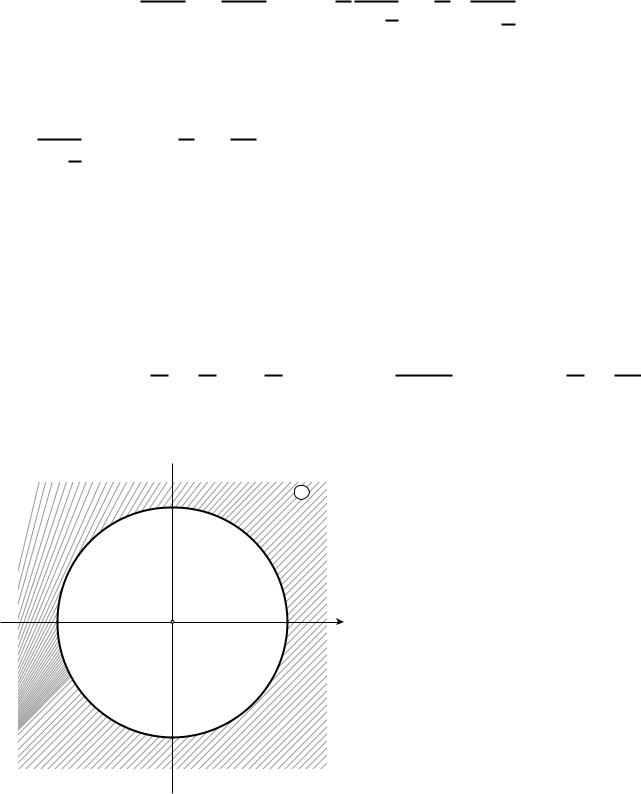
в) |
* |
| | |
+ при |
y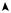
z
z0=0
2 x
