
Lektsia_23
.pdf
Теорія функції комплексної змінної
Лекція 23. Комплексні числа і дії над ними. Множини на комплексній площині. Поняття функції комплексної змінної.
Комплексні числа і дії над ними.
Комплексним числом називається вираз виду
Рис. 1
(алгебраїчна форма комплексного числа), де і – дійсні числа, а – уявна одиниця, яка задовольняє умову . Числа і називаються відповідно дійсною і уявною частинами комплексного числа і позначаються

Комплексне число ̅ |
називається |
|
спряженим числу |
. |
|
Комплексні числа зручно зображати точками |
||
площини. А саме, числу |
ставлять у |
|
відповідність точку з координатами |
(аффікс числа |
|
). |
|
|
Таким чином, має місце взаємно однозначна відповідність між множиною комплексних чисел і множиною точок площини.
Комплексні числа інколи зображають радіусомвектором. Довжина вектора ̅̅̅̅̅ називається модулем комплексного числа і позначається :
√
Кут , утворений вектором ̅̅̅̅̅ з віссю називається аргументом комплексного числа і позначається через
він визначається неоднозначно, а з точністю до доданка, кратного :
( |
) |
де |
– головне значення |
, |

Причому
{
Дії над комплексними числами.
Нехай |
, |
|
. |
|
Тоді |
|
|
|
|
( |
) |
( |
) |
(2) |
( |
) ( |
) |
|
(3) |
|
|
( |
)( |
) |
|
|
( |
) |
|
( |
|
) ( |
) |
(4) |
враховуючи, що |
|
|
|
|
̅ ( |
)( |
) |
|
(5) |
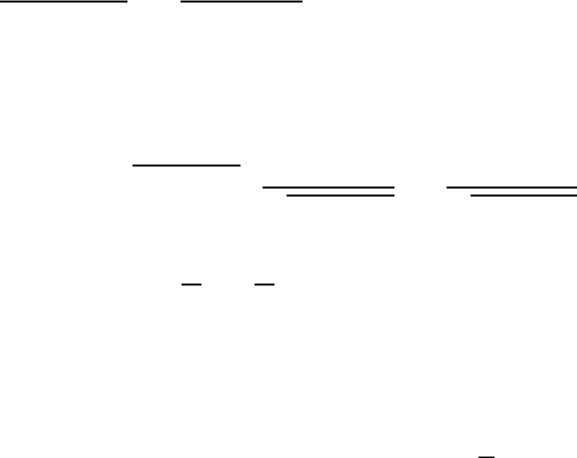
|
|
|
|
|
̅ |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
̅ |
||
|
( |
)( |
) |
|
|||
|
|
|
|
|
|||
|
( |
)( |
) |
||||
|
|
( |
) |
||||
|
|
|
|
|
|
|
|
.
Комплексне число вигляді
√ (√
( ) (
Подання комплексного числа
(
де √ |
|
; |
|
; |
|
(6)
можна подати в
)
√
)
в вигляді
)
називається
тригонометричною формою комплексного числа.
Нехай комплексні числа |
і |
задані в |
|
|||||||||||
тригонометричній формі |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
( |
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
) |
|
|
Тоді |
|
|
|
|
|
|
|
|||||||
[ |
( |
|
|
) |
( |
)] |
||||||||
тобто |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
( |
|
) |
|
|||
|
|
|
|
|
|
[ |
( |
|
|
) |
( |
)] |
||
|
|
|||||||||||||
тобто |
|
|
|
|
|
|
|
|||||||
| |
|
| |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||
( |
|
|
|
|
|
|
) |
|
|
|
(7) |
|||
тобто |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
) |
З рівності ( 7 ) одержуємо формулу Муавра |
||||||||||||||
( |
|
|
|
|
|
|
) |
|
|
|
|
|
||
Множини на комплексній площині
y
z=x+iy z
z0
=x0+iy0
O |
x |
Рис. 2
Нехай – довільне комплексне число. Множина точок комплексної площини, яка задовольняє нерівність
є відкритим кругом радіуса з центром в точці .
|
|
|
|
|
|
√( |
) ( |
) |
|
( |
) ( |
) |
|
|
Означення.Сукупність точок комплексної площини, яка задовольняє нерівність
будемо називати |
-околом точки . |
Означення.Точка називається внутрішньою |
|
точкою множини |
на комплексній площині, якщо |
-окіл цієї точки, який повністю належить даній множині.
Означення.Множина |
називається областю, якщо |
||
виконуються наступні умови: |
|
||
1) |
кожна точка множини |
– внутрішня |
|
2) |
любі дві точки множини |
можна з’єднати |
|
|
ломаною, всі точки якої належать (зв’язність). |
||
|
Надалі область будемо позначати буквою |
||
Означення.Граничною точкою області |
|||
називається всяка точка |
, в |
-околі якої містяться |
|
як точки, які належать області , так і точки, які не належать області .
Означення.Область з приєднаною до неї границею називається замкнутою областю і позначається ̅.
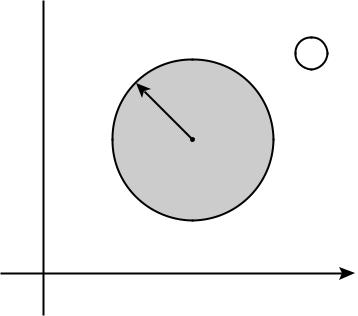
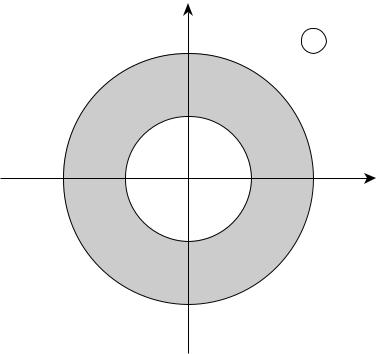
Приклад. Множина точок , які задовольняють умову
є відкритою областю, а нерівність |
– |
замкнутою областю. |
|
y |
|
|
z |
O |
1 |
2 x |
Рис. 3
Границею є два кола |
. |
Означення. Однозначна функція комплексної змінної , заданої в області , визначається законом,
який ставить у відповідність кожному значенню із
області |
в відповідність певне комплексне число: |
||
|
( |
) |
|
Множина комплексних чисел |
яка відповідає |
||
всім |
називається множиною значень функції |
||
( ). |
|
|
|
Якщо кожному числу |
ставиться у |
||
відповідність тільки одне число |
, то функція |
||
|
( |
) |
|
називається однозначною, в противному разі
многозначною.
