
Lektsia_3
.pdfЛекція 3. Застосування подвійних інтегралів.
1. Об’єм тіла. Об’єм циліндричного тіла, твірні якого паралельні осі |
і |
|
яке обмежене знизу областю площини, а зверху поверхнею |
, |
|
знаходиться за формулою: |
|
|
|
|
(1) |
|
|
|
2. Площа плоскої фігури. Нехай у площині |
задана фігура, що має |
|
форму обмеженої замкненої області . У формулі (1) для вирахування |
|
|
об’єму циліндра тіла покладемо |
, тоді одержимо формулу для |
|
вирахування площі: |
|
|
|
(2) |
|
3. Площа поверхні. Якщо поверхня

задана рівнянням |
|
|
, проектується на площину |
в |
|
область |
і функції |
, |
, |
неперервні в цій області, то |
|
площу |
поверхні знаходять за формулою: |
|
|||
√
(3)
|
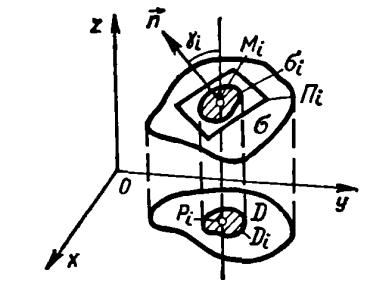
Рис. 1 |
|
|
|
|
|
|
Розіб’ємо область |
на |
частин |
, площі яких дорівнюють |
, |
|||
̅ У кожній частині |
візьмемо точку |
; на поверхні σ їй |
|||||
відповідає |
точка |
|
. |
Через |
точку |
проведемо дотичну |
|
площину |
. Нехай |
– частина дотичної площини, яка проектується на |
|||||
площину |
в області ; |
– її площа. |
|
|
|
||
Границю суми ∑ , якщо найбільший з діаметрів прямує до
нуля, назвемо площею поверхні:
∑ |
(4) |
Площа проекції |
|
, |
де – кут між площиною |
та дотичною площиною. |
|
Вектор нормалі |
до поверхні, |
яка визначається рівнянням |
записується наступним чином: |
||
|
|
. |
Якщо поверхня задана рівнянням |
, тоді |
|
, |
, |
. |

√
Тоді
√
Тому, враховуючи (5):
√
Підставимо (6) в (4):
∑ √
.
(5)
(6)

Під знаком границі маємо інтегральну суму, складену для неперервної
в області |
функції √ |
|
. Ця функція інтегровна в |
області . Тому існує границя і дорівнює подвійному інтегралу
√
Застосування подвійного інтегралу до задач механіки
1.Маса пластини. Нехай на площині маємо матеріальну пластину, яка має
форму обмеженої замкненої області , в кожній точці якої густина визначається

неперервною функцією |
тоді маса пластини визначається за |
формулою |
|
|
|
2.Центр маси пластини. Статичні моменти |
|
|
||
Статичні моменти |
і |
пластинки відносно осей |
і |
визначаються за |
формулами |
|
|
|
|
|
|
Координати і центра мас пластинки знаходять за формулами
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.Моменти інерції пластини відносно координатних осей |
|
|
Моменти інерції |
пластинки відносно осей |
і початку координат |
(полярний момент інерції) відповідно дорівнюють |
|
|
|
|
|
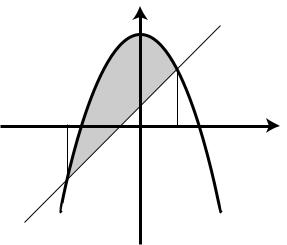
Приклад 1. |
|
Знайти площу фігури, обмеженої лініями: |
, |
y
|
2 |
|
|
x |
|
|
− |
|
|
2 |
|
= |
||
y |
D |
|
−2 |
||
|
||
 A
A
=x y
 B
B
1 x
Визначимо межі інтегрування
{
;
∫ ∫ |
∫ | |
∫ |
( |
|
|
|
|
|
|
|
) | |
|||
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
