
Lektsia_5
.pdfЛекція 5. Заміна змінних в потрійному інтегралі. Застосування потрійних інтегралів.
Розглянемо дві |
замкнуті області |
і |
в |
просторах з прямокутною |
системою координат |
і системою координат |
. |
||
Нехай ці області зв’язані між собою взаємно однозначним
відображенням, яке встановлюється формулами:
|
( |
) |
{ |
( |
) |
|
( |
) |

Нехай ці функції мають в області |
неперервні частинні похідні, якобіан в |
області не дорівнює нулю: |
|
| |
( |
) |
|
|
|
|
|
(1) |
|
|
|
| |
і ( |
) – неперервна в , тоді справедлива формула: |
|
|
( |
) |
(2)
( ( ) ( ) ( ))

|| |
|
|| |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|| |
|
|
|
|
|
|
|| |
|
|
Якщо |
ортогональні координати, тоді |
Перехід до циліндричних координат |
|
|
|
|
||
В площині |
|
введемо полярні координати ( |
|
). Довільно візьмемо |
||
точку ( |
), |
спроектуємо її на площину |
. |
( |
) – проекція цієї |
|
точки, |
|
– полярний радіус, |
– полярний кут точки |
, є |
||
. Числа ( |
) – називаються циліндричними координатами точки . |
|||||
Зв’язок з декартовими координатами: |
|
|
|
|
||
{
, |
, |
. |
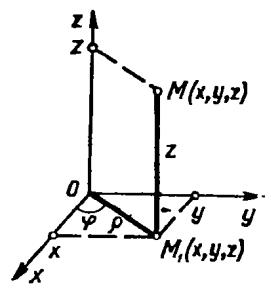
Рис. 1
( |
) |
| |
| |
| |
| |
. |
|
|
|
|
|
З формули (2) отримаємо потрійний інтеграл в циліндричній системі
координат:
( ) ( |
) |
Перехід до сферичних координат. |
|
|
|
||||||
Нехай |
( |
) – довільна точка в просторі, |
( |
) – проекція точки |
|||||
на |
площину |
|
. |
– радіус-вектор |
. |
Тобто, |
відстань від початку |
||
координат до точки |
: |
|
. – радіанна міра кута між променем |
||||||
і додатнім променем осі |
|
, |
. – кут між радіусом-вектором з |
||||||
віссю |
(полярною віссю), |
. |
|
|
|
||||
Числа |
( |
) |
будемо |
називати сферичними координатами точки . |
|||||
Зв’язок з декартовими координатами: |
|
|
|
||||||
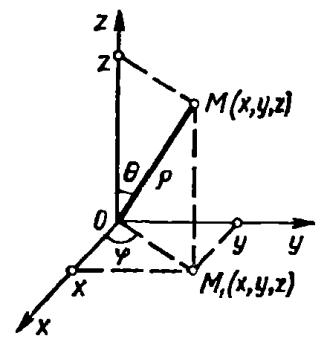
{
; |
; |
. |
Рис. 2
| |
| |
. |
Зформули (2) знаходимо потрійний інтеграл у сферичних координатах:
( )
(3)
( |
) |
Застосування потрійного інтегралу
Нехай маємо деяке тіло, обмежене замкненою областю , що має об’єм
, тоді формула вирахування об’єму тіла:
Маса тіла.
Якщо задане тіло має постійну густину , тоді маса пропорційна об’єму тіла:
Якщо тіло має густину |
( |
), |
|
де ( |
) – неперервна функція в області , тоді |
||
|
|
|
|
Моменти інерції , , |
тіла відносно координат осей |
, |
, |
відповідно дорівнюють: |
|
|
|
( )
( )
( )
Моменти інерції |
, |
, |
тіла відносно координатних площин |
, |
,обчислюються за формулами
