
Lektsia_27
.pdfЛекція 27. Числові ряди з комплексними членами.Степеневі ряди. Ряди Тейлора.
Числові ряди
Розглянемо ряд
∑ |
(1) |
з комплексними членами
Означення.Якщо послідовність його частинних сум
∑
має границю , то цю границю називають сумою ряду
(1).
Збіжність комплексного ряду
∑ ∑( )
до суми |
рівносильна збіжності двох рядів з |
дійсними членами |
|
∑ ∑ |
(2) |
до суми |
відповідно. |
Означення.Ряд (1) називається абсолютно збіжним, якщо збігається ряд із модулів
∑| | |
(3) |
Ряди (2) і (3) є рядами з дійсними членами. Питання збіжності вирішується за допомогою ознак збіжності для рядів з дійсними членами.
Функціональні ряди
Вираз вигляду
∑( )
будемо називати функціональним рядом.
Дуже важливими є функціональні ряди, для яких ( ) ( ) , де – деякі комплексні числа,
– фіксована точка комплексної площини. Такі ряди називаються степеневими.
Розглянемо степеневий ряд
|
|
∑ |
( |
|
) |
(4) |
|
Теорема Абеля . Якщо ряд (4) збіжний в точці |
|
||||||
|
|
, то він абсолютно збіжний і при всіх |
|
||||
значеннях |
, для яких | |
| |
. Якщо ряд (4) розбіжний |
||||
в точці |
|
, то він розбіжний і при всіх значеннях |
, |
||||
для яких |
| |
| | |
| |
|
|
|
|
|
|
. |
|
|
|
|
|
Із теореми Абеля випливає існування такого числа |
|||||||
, що для всіх | |
| |
степеневий ряд абсолютно |
|
||||
збіжний, а при | |
| |
|
– розбіжний. |
|
|||
Таким чином ми маємо :
1)при |
ряд буде збіжним на всій комплексній |
|
площині, |
|
|
2)при |
- ряд збіжний абсолютно всередині |
|
кола радіуса |
, і розбіжний за межами цього кола. |
|
Якщо ряд (4) збіжний лише в точці |
, то |
|
вважають |
. |
|
Радіус збіжності степеневого ряду |
|
|
∑( )
визначається формулою
|
|
, |
|
|
|
|
|||
|
|
|
(5) |
|
де |
| | |
|||
|
√ |
|||
або
Ряд Тейлора |
|
|
|
| |
|
|
| |
|
(6) |
||||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||
Теорема Тейлора. Функція ( |
) аналітична всередині |
||||||||||||
кола | |
| |
може бути представлена в цьому |
|||||||||||
колі збіжним степеневим рядом |
|
|
|||||||||||
( ) |
∑ |
( |
|
|
) , причому цей ряд визначений |
||||||||
однозначно. |
|
|
|
|
|
|
|
|
|
|
|||
Коефіцієнти |
вираховуються за формулами |
||||||||||||
|
|
|
|
( ) |
|
|
|
( )( ) |
( |
) |
|||
|
|
( |
) |
|
|
|
|
|
|||||
де |
коло з центром в точці |
|
, яке повністю |
||||||||||
лежить в околі точки |
|
в якому функція |
( ) |
||||||||||
аналітична.

Розклад в ряд Тейлора елементарних функцій комплексної змінної.
∑
( )
∑ ( )
|
∑ |
( ) |
|
|
|
|
|
( ) |
|
|
|
||
Формули (7) – (9) справедливі для |
|
, тобто |
||||
( |
) ∑ |
( ) |
|
| | |
||
|
||||||
Біноміальний ряд
( ) ∑ |
( ) ( |
) |
|
|
(7)
(8)
(9)
.
(10)

( |
) |
( |
) ( |
) |
+ |
||||
|
|
|
|
|
|
|
|
|
|
; | | |
|
|
|
|
|
|
|||
|
|
|
|
|
|
(11) |
|||
Частинні випадки біноміального ряду
( |
) |
| | |
(12)
| |
(13)
Формули (10)- (13) справедливі для | | |
. |
|
Приклад 1.Вирахувати |
|
|
∫( |
̅) |
|
де – відрізок, який з’єднує точки
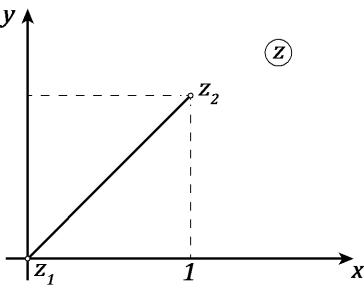
Рис. 1
̅
( )
∫( |
) ( |
) |
∫( |
) |
( |
) |
| |
| ∫( |
) |
∫( |
) |
∫ |
∫ |
( ) |
Приклад 2. Вирахувати інтеграл
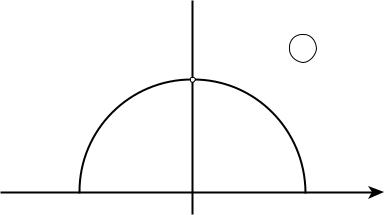
∫( ̅)
де – дуга кола | | |
( |
)) |
y
1 z
1 x
Рис. 2
Параметричне рівняння кола має вигляд
̅
∫( |
̅) |
∫( |
) |

∫( |
) |
( |
|
|
|
) | |
|
|
|||||
( |
|
) | |
|
|
|
|
|
|
|
|
|||
[ |
|
( |
|
)] | |
|
|
Приклад 3. Вирахувати
∫
де – коло з центром |
і радіусом рівним а)1; б)5. |
а)
y
z
−3 |
1 |
x |
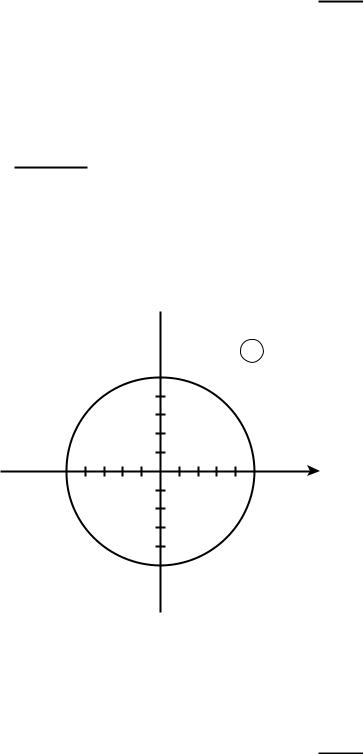
Рис. 3
Якщо – коло, радіусу 1, то функція аналітична в кожній точці круга | | . Тоді, застосовуючи теорему Коші
∫
б)
y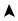
5 z
5
−3 |
x |
|
Рис. 4
Якщо – коло радіусу 5, тоді точка належить колу | | . В цій точці функція не визначена і не аналітична.
Таким чином, теорему Коші для вирахування інтегралу застосовувати не можна.
