
Lektsia_22
.pdfЛекція 22. Ортогональна система функцій. Ряд Фур’є за ортогональною системою функцій.
Означення. Дві функції |
і |
, визначені на |
|
проміжку |
називаються ортогональними в цьому |
||
проміжку, якщо їх добуток має інтеграл рівний нулю
∫
Нехай на відрізку |
задано нескінченну |
систему функцій |
|
(1)
інтегрованих в цьому проміжку разом з їх квадратами.
Тоді, якщо функції даної системи попарно ортогональні
∫
і виконується умова
для
∫

то її будемо називати ортогональною системою функцій на .
Якщо при цьому буде виконуватися умова тоді розглянута вище система функцій
називається ортонормованою.
Якщо ця умова не виконується, тоді можна перейти до системи функцій
√
яка буде ортонормованою.
Важливим прикладом ортогональної системи функцій є тригонометрична система
(2)
в проміжку |
. |
∫ |
∫ |
∫ ∫
одержуємо, що система функцій (2) – ортогональна.

Помноживши тригонометричні функції (2) на певні множники, одержуємо ортонормовану систему:
√ √ √ √ √
Системи функцій
і
будуть ортогональними на відрізку |
. |
Системи функцій
і
будуть ортогональними на відрізку |
. |
|
|
Нехай функція |
розкладається в ряд за |
|
|
функціями ортогональної системи (1) |
|
|
|
|
∑ |
|
(3) |
Нехай ряд (3) – рівномірно збіжний на |
. |
||
Визначимо коефіцієнти |
. Помножимо обидві |
частини рівності (3) на |
і результат почленно |
проінтегруємо |
|
∫ |
∫ |
∫
(4)
∫
Ряд (3) називають рядом Фур’є функції за системою ортогональних функцій (1), а коефіцієнти цього ряду, коефіцієнтами Фур’є.
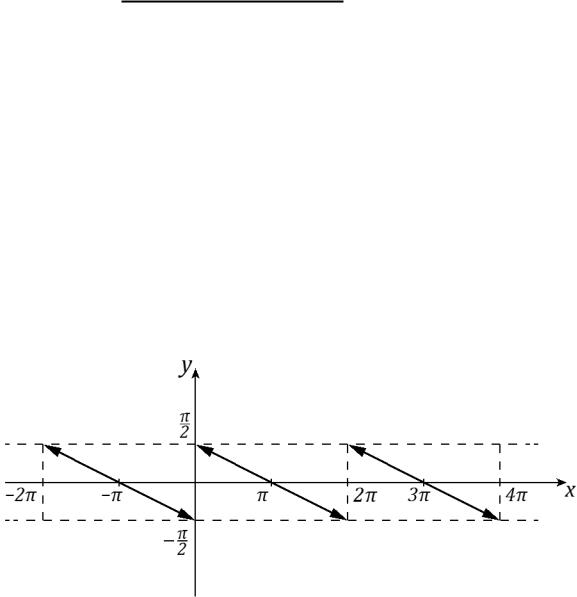
Приклад 1. |
|
|
|
Розкласти |
-періодичну функцію |
|
в ряд |
|
|||
Фур’є на відрізку |
. |
|
|
Використовуючи формули (
∫ |
|
∫ |
|
∫
∫ |
|
|
|
( |
|
) | |
|
|
|
∫
| |
| |
|
|
|
|
| ∫
∫ |
|
|
|
|
|
| |
|
|
|

∫
∑
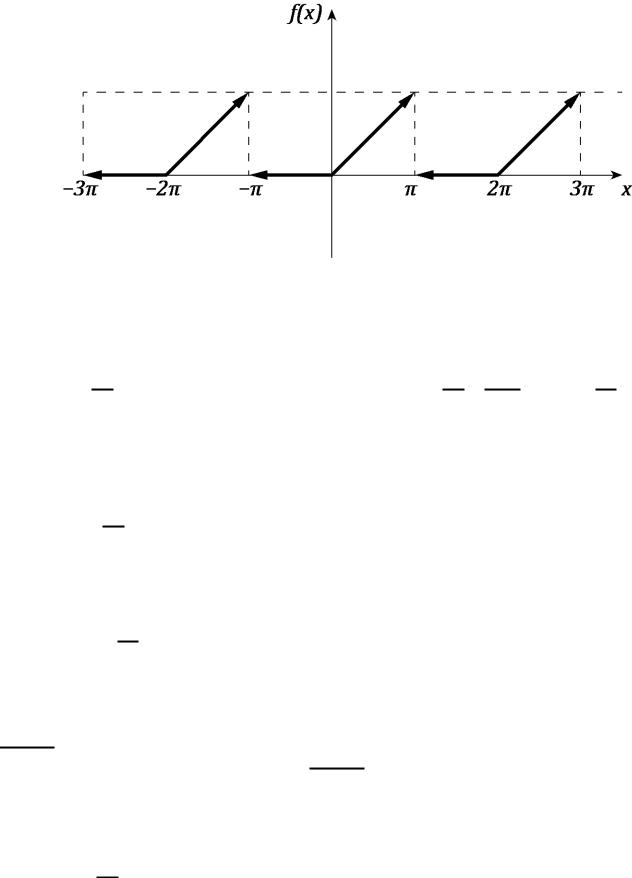
Приклад 2.
Розкласти в ряд Фур’є функцію періоду .
{ |
|
Задана функція на відрізку |
–кусково- |
монотонна і має в точках |
розриви |
першого роду, тобто задовольняє умови теореми Діріхле,
Обчислимо коефіцієнти Фур’є: |
|
|
( ∫ |
∫ ) |
| |
( ∫ |
∫ |
) |
( |
|
| |
|
| ) |
|
|
{
( ∫ |
∫ |
) |

( |
|
| |
|
| ) |
|
|
| |
| |
Запишемо розклад в ряд Фур’є:
∑ ∑
У точках розриву сума ряду
Отже ( |
) |
Приклад 3.
Розвинемо в ряд Фур’є функцію
| |

Функція неперервна , функція кусково-монотонна, тобто задовольняє умови теореми Діріхле.
∫ |
|
| |
|
∫ |
|
∫ |
|
| |
| |
|
( |
|
|
|
) | |
|
|
|
( |
|
|
|
) |
|
|
{

При
∫ |
|
∫ |
|
|
Отже,
∑
Для
