
Lektsia_20
.pdfТригонометричні ряди Фур’є.
Лекція 20. Гармонічні коливання. Розклад в ряд Фур’є
періодичної функціі. Коефіцієнти Фур’є.
Гармонічні коливання.
Функція називається періодичною з періодом , якщо вона визначена на всій числовій осі і для
неї виконується рівність
Найпростішою із періодичних функцій є функція
|
|
(1) |
де |
, |
– початкова фаза, – амплітуда, – |
період. |
|
|
Функцію (1) називають простою гармонікою.
Якщо скласти декілька величин вигляду
(2)
з частотами |
і періодами |
|
|
|
то |
|
|
||||
одержимо періодичну функцію (з періодом |
), але вже |
||||
суттєво відмінну від величин типу (2). |
|
|
|
||
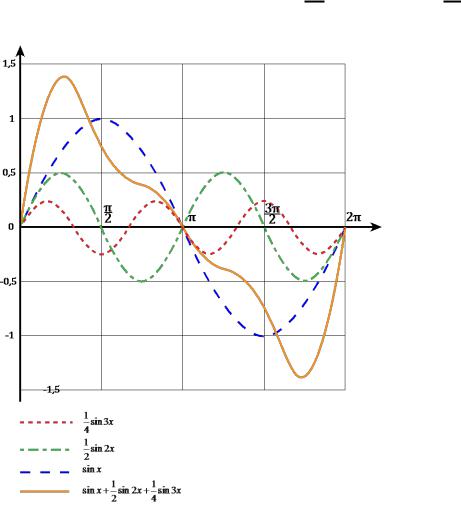
Коливання, утворені внаслідок накладання простих гармонік, називають складними гармонічними коливаннями.
Приклад.
Рис. 1

Природно, постає обернене питання: чи можна дану періодичну функцію подати у вигляді суми простих гармонік (2)?
Якщо використати нескінченну послідовність величин (2), то для досить широкого класу функцій це можна зробити.
Для функцій цього класу має місце розклад в тригонометричний ряд
∑ ( )
(3)
( |
) |
|
|
|
|
|
( |
) |
|
|
|
|
|
Якщо покласти |
|
|
, тоді |
( |
|
). |
|
|
|
∑ ( )
Нехай

∑
Розклад в ряд Фур’є періодичної функціі. Коефіцієнти Фур’є.
Ряд вигляду
(4)
∑
називається тригонометричним рядом, а дійсні числа
– його коефіцієнтами.
Нехай функція – інтегровна на відрізку
. Допустимо, що розклад (4) має місце і проінтегруємо почленно на відрізку
∫
∑ ( ∫ |
∫ |
) |
Так як

∫ |
|
| |
|
∫ |
|
| |
|
Одержуємо
∫
Для вирахування коефіцієнтів |
помножимо |
обидві частини рівності (4) на |
і проінтегруємо |
одержаний ряд почленно на відрізку
∫
∫
∑ ( ∫ |
∫ |
) |
Якщо
∫ |
|
∫ |
|
∫ |
|
∫ |
|
Якщо
∫ ∫
∫
Аналогічно, помноживши рівність (4) на |
і |
проінтегрувавши почленно на відрізку |
, |
знайдемо |
|
∫
Формули Ейлера–Фур’є
∫
(5)
∫

∫
Числа – які визначаються за цими формулами (5) називаються коефіцієнтами Фур’є.
Тригонометричний ряд (4), коефіцієнтами якого є коефіцієнти Фур’є функції , називають рядом Фур’є цієї функції і записують
∑
Знак відповідності означає, що інтегровній на
відрізку |
функції |
поставлено у |
відповідність її ряд Фур’є. |
|
|
Теорема . Якщо функцію |
можна подати на |
|
відрізку |
у вигляді рівномірно збіжного на |
|
цьому відрізку тригонометричного ряду (4), то цей тригонометричний ряд єдиний і є рядом Фур’є для функції .
З’ясуємо умови, за яких знак відповідності у формулі (4) можна замінити знаком рівності, тобто, за

яких ряд Фур’є функції є збіжним і має своєю сумою саме функцію .
Теорема Діріхлe. (Достатня умова подання функції через її ряд Фур’є)
Якщо періодична функція |
з періодом |
є |
1)неперервною на відрізку |
або має на цьому |
|
відрізку скінченне число точок розриву першого роду;
2)кусково-монотонною; |
|
|
тоді її ряд Фур’є функції |
збігається |
|
1) до суми |
= |
в кожній точці неперервності |
функції і |
|
|
2)до суми
вкожній точці розриву.
3) В кінцевих точках відрізка |
сума ряду |
||
Фур’є набуває значень |
|
|
|
|
|
|
|

Зауваження 1. |
|
|
Якщо ряд (4) збіжний до функції |
на відрізку |
|
, то він збігатиметься до цієї самої функції на |
||
всій числовій осі |
; при цьому |
|
. Отже, функцію, задану на відрізку та періодично продовжену на всю числову
пряму, можна подати через суму ряду Фур’є.
Зауваження 2.
При періодичному продовженні функції
на всю числову вісь знайдена функція буде або неперервною в точках
, або розривною в цих точках.
Неперервність можлива лише, якщо
|
. У цьому разі сума ряду Фур’є |
дорівнює |
. |
|
y |
−π 0 π |
3π |
x |
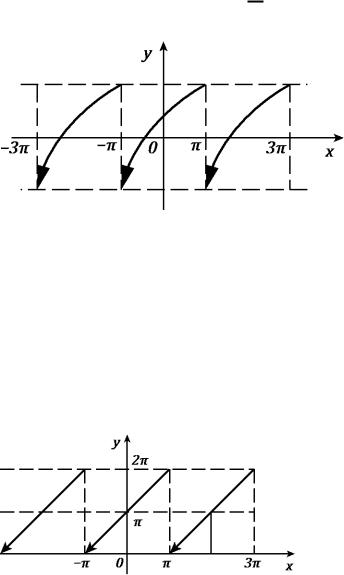
Рис. 2
Якщо ж |
, то ми можемо залишити |
|
без зміни значення функції на проміжку |
і |
|
періодично з періодом |
продовжити її на всю |
|
числову вісь. |
|
|
При цьому в точках |
|
, можуть |
виникнути точки розриву першого роду, в яких сума ряду Фур’є дорівнює
.
Рис. 3
Приклад1.
Розкласти в ряд Фур’є -періодичну функцію:
