
Lektsia_14
.pdfЛекція 14
Достатні ознаки збіжності ряду. Теореми порівняння. Ознака Даламбера, радикальна ознака Коші, ознака Раабе. Інтегральна ознака Маклорена-Коші.
Теорема (перша ознака порівняння).
|
|
|
|
|
|
|
|
|
Нехай для рядів |
un |
і |
vn |
з додатними членами |
, |
, |
||
n 1 |
n 1 |
|||||||
|
|
|
|
|
|
|||
для |
виконується умова |
|
|
|
||||
починаючи з деякого номера |
. Тоді: |
|||
|
|
|
|
|
а) якщо ряд |
vn |
збігається, тоді збігається і ряд |
un . |
|
|
n 1 |
|
|
n 1 |

|
|
|
|
|
|
|
б) якщо ряд |
un розбігається, тоді розбігається і ряд |
vn . |
|
|||
|
n1 |
|
|
n 1 |
|
|
|
|
|
|
|
|
|
Якщо ряд |
un |
збігається, тоді про збіжність ряду |
vn |
нічого не |
||
|
|
n1 |
|
|
n 1 |
|
можна сказати. Якщо ряд vn – розбігається, тоді не можна говорити
n 1
про розбіжність ряду n1 un .
Теорема (друга ознака порівняння)
|
|
|
|
|
|
Нехай задано два ряди |
un |
, |
vn |
з додатними членам, причому |
|
n1 |
n 1 |
||||
|
|
|
. Розглянемо границю відношення загальних членів цих рядів.

Тоді
|
|
|
|
|
|
якщо |
( – скінченне додатне число), тоді ряди |
un |
і |
vn |
|
n1 |
n 1 |
||||
|
|
|
збігаються (розбігаються) одночасно, тобто коли один збігається (розбігається), тоді збігається (розбігається) і другий ряд;
Приклад 1. Дослідити на збіжність ряд
∑
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
Позначимо |
|
. Для порівняння візьмемо ряд |
n2 . Тоді |
||||
|
n 1 |
||||||
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
||
Отже, за першою ознакою порівняння цей ряд збігається.
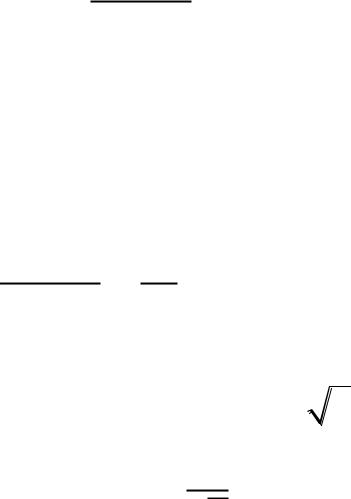
Приклад 2. Дослідити на збіжність ряд
∑
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
. Візьмемо за порівняльний ряд |
2n . Цей ряд збігається |
||||
|
n1 |
||||||
як геометричний ( |
|
) |
|
|
|
||
|
|
|
|
||||
|
|
|
1 |
|||
|
1 cos |
|
|
|
|
|
|
|
|
|
|||
|
|
|
||||
Приклад 3. Дослідити на збіжність ряд |
n1 |
|
|
n . |
||
√
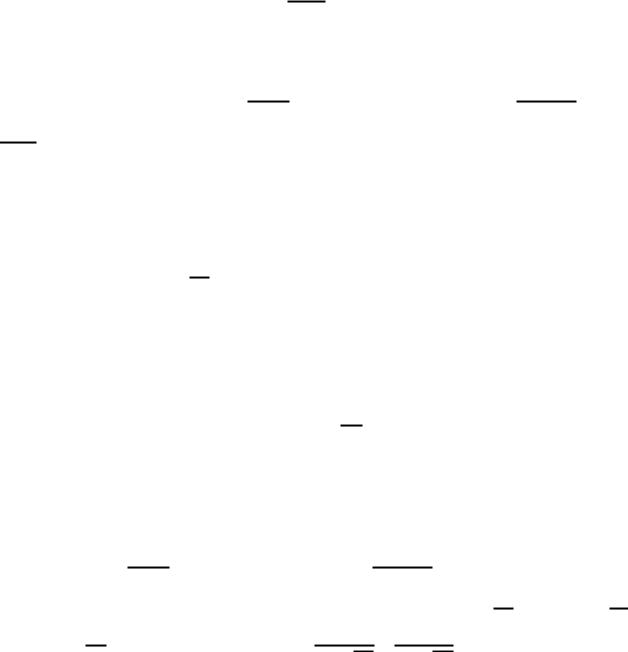
1
Виберемо для порівняння ряд n1 n2 . Цей ряд збіжний.
|
|
√ |
|
|
|
|
√ |
|
|
|||||||
|
|
|
|
|
( |
|
|
|
) |
( |
|
|
) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
√ |
|
|
√ |
|
|||||||
|
|
|
|
|
|
|
||||||||||
друга ознака не дає відповіді на запитання про збіжність.
1
Виберемо для порівняння інший ряд n . Цей ряд розбіжний як
n1
гармонічний ряд.
√ |
|
|
|
√ |
|
|
√ √
а порівняльний ряд розбігається, тоді за другою ознакою розбігається досліджуваний ряд.
Достатні ознаки збіжності рядів з додатніми членами
Теорема (Ознака Даламбера)
|
|
|
|
|
|
|
Нехай задано ряд |
un |
з додатними членами |
. Якщо існує |
|||
n1 |
||||||
|
|
|
|
|
||
границя |
|
|
, тоді |
|
||
|
|
|||||
|
|
|
|
|
а) якщо |
, тоді ряд |
un |
– збігається. |
|
n1 |
||||
|
|
|
б) якщо |
, тоді ряд |
n1 |
розбігається. |
|
|
|
|
в) якщо |
, тоді питання про збіжність ряду не вирішене. |
||
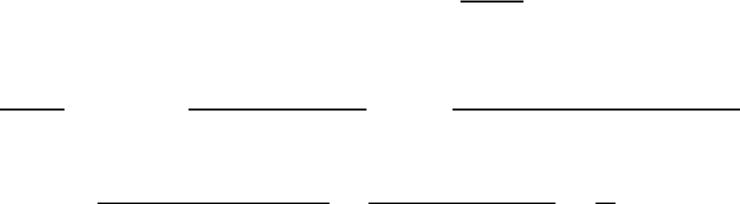
2n n!
Приклад 4. Дослідити на збіжність ряд nn
n1
|
|
|
|
|
( |
|
|
) |
|
( |
|
) |
|
|
|
|
|
|
|
|
|
|
|||||
ряд збігається за ознакою Даламбера |
|
|
|
||||||||||
Теорема (Радикальна ознака Коші) |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
Нехай задано ряд |
un |
з додатними членами |
. Тоді, якщо |
||||||||||
n1 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||
існує границя |
|
|
|
|
|
|
, тоді |
|
|
|
|
||
|
√ |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
а) якщо |
, тоді ряд |
un |
збігається. |
|
|||||||||
n1 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
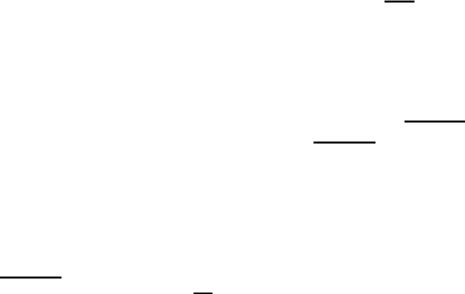
б) якщо |
, тоді ряд |
n1 |
розбігається. |
|
|
|
|
в) якщо |
, тоді питання про збіжність ряду не вирішене. |
||
|
|
|
|
|
2n 5 |
n2 |
|
|
|
|
|
|
|||
Приклад5. Дослідити на збіжність ряд |
|
|
|
|
|||
|
|
||||||
n1 |
|
2n 7 . |
|||||
|
|
|
|
|
|
|
|
√ |
|
√( |
|
) |
( |
|
) |
|
|
|
|||||
|
|
|
( |
|
) |
[( |
|
) |
] |
|
|
Отже, за радикальною ознакою Коші ряд збіжний.
Теорема (Інтегральна ознака Маклорена-Коші).
|
|
|
|
|
Нехай задано ряд |
un |
з додатними членами |
, які не зростають |
|
n1 |
||||
|
|
|
Тоді, якщо функція |
визначена для всіх дійсних |
, неперервна, |
|||
|
|
|
|
|
|
незростаюча і така, що |
, тоді ряд |
un |
і невласний інтеграл |
||
n1 |
|||||
|
|
|
|
||
f (x)dx одночасно збігаються або розбігаються.
1
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
Приклад 7. Дослідити на збіжність ряд |
3n 5 . |
|
|||||
n1 |
|
||||||
Оскільки функція |
|
|
додатна при |
і не зростає, то можна |
|||
|
|||||||
використати інтегральну ознаку: |
|
|
|
|
|
||

∫ |
|
|
|
| |
|
[ |
] |
|
|
|
Отже, невласний інтеграл розбіжний, а тому і ряд теж розбіжний
Приклад. Дослідити на збіжність узагальнений гармонічний ряд, який ще називають рядом Діріхлe .
∑
1) Якщо |
: ∑ |
|
– гармонічний ряд розбіжний. |
|
|
||||
2)Дослідимо ряд при |
|
і |
|
|
Оскільки функція |
|
|
є знакододатною при |
і не зростає, то можна |
для дослідження ряду ∑ застосовувати інтегральну ознаку
