
Lektsia_10
.pdf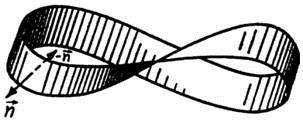
Лекція 10. Поверхневий інтеграл другого роду.
Поверхня, у якої фіксована одна із її сторін називається орієнтовною.
Поверхневі інтеграли дугого роду розглядаються тільки по орієнтовних поверхнях.
Двосторонні поверхні характеризуються такою властивістю: якщо вектор нормалі
неперервно переміщати по будь-якому замкненому контуру , що лежить на поверхні і не перетинає її межу, то при поверненні в вихідну точку напрям
співпадає з початковим.
Якщо напрям змінюється на протилежний – односторонньою (лист Мебіуса).
Нехай |
– орієнтована поверхня. |
а) Якщо |
, тоді говорять про верхню або |
нижню сторону поверхні.
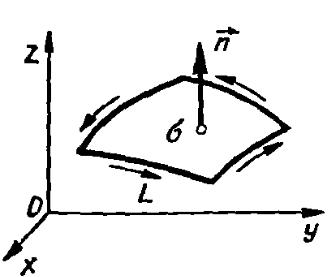
б) Якщо поверхня обмежує дане тіло, тоді говорять про внутрішню або зовнішню сторону.
Додатній напрямок обходу контуру : обхід повинен бути проти годинникової стрілки, тобто спостерігач повинен бачити прилеглу до нього частину поверхні зліва від себе
Найпростішим і важливим прикладом поверхні є поверхня
Нехай в точках цієї поверхні визначена деяка функція
.
Зорієнтуємо поверхню . В даному випадку виберемо верхню або нижню сторону поверхні.

Рис. 1
Розкладемо поверхню сіткою кривих на елементи:
{ |
} |
|
|
. |
|
Виберемо в кожній частині |
довільну точку |
|
|
і складемо суму |
|
Вирахуємо значення функції |
і |
|
помножимо його на площу |
проекції на площину |
|
елемента . Складемо інтегральну суму:
∑ |
∑ |
(1) |
|
|
Нехай |
– максимальний діаметр |
поверхонь . |
|
Якщо при |
інтегральна сума (1) має скінченну |
границю, яка не залежить ні від способу розбиття
поверхні , ні від вибору точок |
то цю границю |
|
називають поверхневим інтегралом другого роду |
||
|
∑ |
(2) |
Якщо проектувати елементи поверхні на площину або , одержимо два інших поверхневих інтеграли другого роду
|
|
(3) |
|
|
На практиці використовують поверхневі інтеграли, які об’єднують усі названі інтеграли (2), (3):
|
(4) |
Вирахування поверхневого інтегралу другого роду.
Нехай гладка поверхня задана рівнянням
. Нехай функція
неперервна у всіх точках цієї поверхні.
Оскільки |
, тоді інтегральна сума (1): |
|
∑ |
( |
) |
(5) |
Ця сума аналогічна інтегральній сумі для для функції |
|
|||
( |
). Тому перейшовши в рівності (5) до |
|
||
границі при |
|
одержимо формулу |
|
|
|
( |
) , |
яка виражає поверхневий інтеграл другого роду по змінних через подвійний.
Знак «+» беремо у цій формулі тоді, коли нормаль до поверхні утворює з віссю гострий кут, а знак «-» , коли тупий кут.
Аналогічно, якщо гладку поверхню задано рівнянням
|
|
або рівнянням
|
|
Знак «+» беремо у цих формулах тоді, коли нормаль до поверхні утворює відповідно з віссю з віссю гострий кут, а знак «-» , коли тупий кут.
Якщо поверхня проектується на всі координатні площини, тоді загальний інтеграл (4) обчислюється через подвійні інтеграли:
|
= |
( |
) |
|
|
Зв’язок поверхневих інтегралів першого і другого роду.
Нехай гладка поверхня задана рівнянням
Напрямні косинуси нормалі до поверхні мають вигляд:
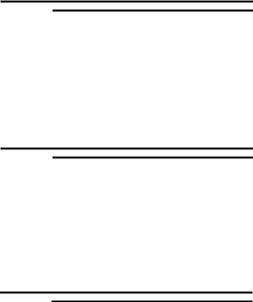
√
√
|
√ |
– кути між нормаллю до поверхні та осями |
|
|
віповідно. |
Якщо кути |
гострі , то у формулах знак « », а |
якщо тупі, то знак « ».
Враховуючи, що |
, |
, |
, |
одержуємо формули вирахування поверхневого інтегралу другого роду за допомогою поверхневого інтегралу першого роду
Тоді (4) набуває вигляду
|
= |
= |
|
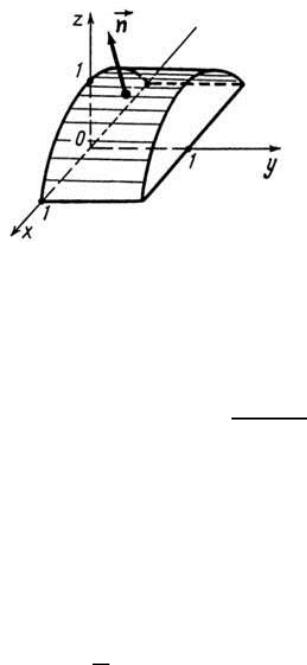
Приклад 1.Обчислити інтеграл ( |
) |
де – |
||
|
|
|
|
|
верхня сторона поверхні |
√ |
, що відтинається |
||
площинами |
. |
|
|
|
.
З урахуванням того, що нормаль до поверхні утворює гострий кут з віссю
( (√ ) )
∫ ∫ |
∫ ( |
|
) | |
|
∫ ( )
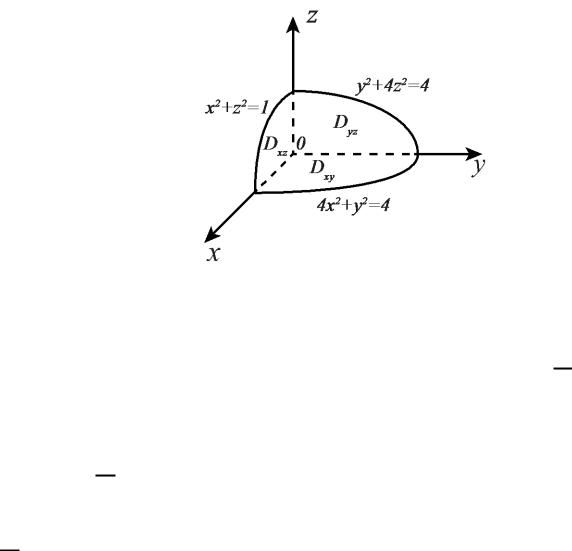
Приклад2.Обчислити поверхневий інтеграл другого роду, де – зовнішня сторона еліпсоїда
.
