1.4.3. Загальні принципи побудови систем числення з паралельним обчисленням символів

Побудова систем числення класу В, куди входить система числення залишкових класів СОК, починають з вибору основи , що обов'язково є цілими, причому, з метою забезпечення однозначності і безперервності подання, набір основ повинен включати , що являє собою взаємно прості числа.

Вибравши основи, можна розраховувати величини :

, де ,

де

- ортогональні базиси, тобто визначити її базис В.

Довільне число Х  визначається набором залишків , де , або ,,. Процес обчислення символів здійснюється незалежно і паралельно по кожній основі . У них первинними параметрами є цілі, взаємно прості основи. При цьому Китайська теорема про залишки гарантує однозначне уявлення чисел   в діапазоні , де .

Формула переведення з СОК в десяткову систему числення має вигляд:

.

В літературі стверджується, що СОК є непозиційною символічною невиваженою системою числення. Приклад перекладу чисел з СОК в десяткову систему числення за допомогою ортогональних базисів, повністю заперечує це твердження. Ця система числення є представником зовсім іншого класу В системах числення, в яких, ще раз підкреслимо, процес знаходження символів, на відміну від систем класу А, здійснюється паралельно і незалежно.

Розглянемо приклад:

Переведення з СЧ залишкових класів чисел зі змішаною основами

Візьмемо число 11 в 753, це буде 412 в цій системі. Будемо розглядати упорядковану СЧ. Тоді Q ₁ = 2. Далі, 412-222 = 240-ділиться на 3 без залишку.

Двійково-десяткова система числення отримала назву 8421 +3, являє собою зміщену на 3 одиниці класичну двійково-десяткову систему 8421. Недопустимо відносити її до "зважених" систем числення, в яких ваги окремих розрядів мають змінні значення.

Якщо позиційна система числення має   (Наприклад ) То будь-який її символ можна представити за допомогою СОК (на приклад для   можна вибрати модулі ,,,, тоді) для кодування цих модулів досить мати 18 двійкових розрядів, що не набагато більше 16. Доцільність такого комбінованого подання пояснюється можливістю реалізації суматора, в якому перенос буде поширюватися не більше, ніж на 5 розрядів.

1.5. Кодування знакозмінної інформації. Коротка характеристика груп кодів, родинних прямому, зворотному, додатковому. Особливості застосування в комп'ютерах

Знакозмінна інформація на числовій осі займає дві ділянки. Ділянка, розташованa праворуч від нуля, використовується для представлення додатніх чисел, ліворуч - для від’ємних.

При кодуванні такої інформації в обчислювальних системах використовуються також дві ділянки числової осі, розташовані праворуч від нуля. Ці ділянки будемо називати відповідно областю зображення додатніх чисел і областю зображення від'ємних чисел. Знак інформації кодується за допомогою додаткового розряду, що є покажчиком відповідної області зображення. Цей розряд, званий знаком, розташовується лівіше старшого значущого розряду (ЗЗР). Якщо молодший значущий розряд (МЗР) має вагу , а СЗР - вага , то знакової розряду присвоюється природна вага .

Існують два принципи кодування знакозмінних величин:

- Принцип зсуву, при якому будь-яка величина з обраного для обчислювального пристрою діапазону подання чисел кодується як

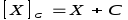(1.1)

де   - код величини Х, С  - постійна величина, яка називається зсувом;

- Принцип доповнення, коли

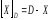(1.2)

де   - Постійна величина, яка називається доповненням.

Пропонуємо такі способи кодування цифрової знакозмінної інформації, що використовують ці принципи.

1. Коди зі зміщенням ( С-Коди):

а) коди зі зміщенням обох областей ( СС-Коди)

(1.3)

б) коди зі зміщенням тільки у від’ємній області ( ZC-Коди)

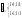(1.4)

2. Коди з доповненням ( D-Коди):

а) коди, в яких обидва доповнення відмінні від нуля (DD-Коди),

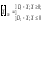(1.5)

б) коди, в яких негативні числа доповнюються до нуля ( DZ-Коди),

(1.6)

3. Коди зі зміщенням і доповненням - комбіновані коди ( K-Коди):

а) CD-Код

(1.7)

б) ZD-Код

(1.8)

в) CZ-Код

(1.9)

г) DC-Код

(1.10)

Відзначимо, що значення величин зміщень і доповнень повинні вибиратися з урахуванням таких обмежень:

1) області зображень додатніх і від’ємних чисел не повинні перетинатися;

2) коди для зображень додатніх і від’ємних чисел повинні мати різну інформацію в знаковому розряді.

Виняток допускається тільки при зображенні нуля. Нуль може бути представлений або одним, або двома різними кодами.

З урахуванням викладених обмежень для двійкової системи числення з природним порядком проходження ваг були знайдені всі можливі величини зміщень і доповнень і побудовані відповідно до цього С-, D- і K-коди (таблиця 1.1).

Таблиця 1. 1. Знакозмінні двійкові коди

Тип коду	Позначе-ння коду	Величина зсуву та доповнення	Найменування коду
С	СС 1		Додатковий з інверсним знаком (зміщений)
	CC 2		Інверсний додатковому мінус числа з інверсним знаком
	CC 3		Зворотній з інверсним знаком
	CC 4		Інверсний додатковому (інверсія коду з доповненням до 2)
	ZC 1		Зворотній (з доповненням до одиниць)
	ZC 2		Додатковий (з доповненням до 2)
D	DD 1		Додатковий мінус числа з інверсним знаком
	DD 2		Інверсний додаткового, крім знака (інверсія двійкового коду зі зміщенням)
	DD 3		Інверсний зворотному, крім знака
	DD 4		Інверсний додатковому мінус числа
	DZ 1		Додатковий мінус числа (з доповненням до 2 позитивній області)
	DZ 2		Інверсний зворотному (інверсія коду з додатком до одиниць)
K	DC 1		Інверсний прямому (інверсія коду знак + модуль числа)
	DC 2		Інверсний прямому, крім знака
	ZD		Прямий (знак + модуль числа)
	CZ		Прямий з інверсним знаком

На рисунках 1.2 - 1.4 наведена геометрична інтерпретація знайдених двійкових кодів і показано зв'язок чисел з їх зображенням (кодами). Крім того, в таблицях 1.2 - 1.4 наведені приклади кодування додатніх та від'ємних граничних значень, ЗЗР, МЗР і нуля.

Рис. 1.2 - Геометрична інтерпретація кодів зі зміщенням

Рис. 1.3 - Геометрична інтерпретація кодів з доповненням

Рис. 1.4 - Геометрична інтерпретація кодів зі зміщенням і доповненням

Таблиця 1. 2. Коди зі зміщенням

Число	СС 1	CC 2	CC 3	CC 4	ZC 1	ZC 2
-0,11...11	0.00...01	0,00...00	0,00...00	0,11 ... 10	1,00 ... 00	1,00 ... 01
-0,10...00	0,10...01	0,01...11	0,01...11	0,01 ... 11	1.01 ... 11	1,10 ... 00
-0,01...11	0,10...01	0,10...00	0,10...00	0,01 ... 10	1.10 ... 00	1,10 ... 01
-0,00...01	0,11...11	0,11...10	0,11...10	0,00 ... 00	1,11 ... 10	1,11 ... 11
-0,00...00	1,00...00	0,11...11	0,11...11	1,11 ... 11	1,11 ... 11	0,00 ... 00
+0,00…00	1,00...00	0,11...11	1,00...00	1,11 ... 11	0,00 ... 00	0,00 ... 00
+0,00... 01	1,00...01	1.00...00	1,00...01	1,11 ... 10	0,00 ... 01	0,00 ... 01
+0,01... 11	1,01...11	1,01...10	1,01...11	1,10 ... 00	0,01 ... 11	0,01 ... 11
+0,10...00	110...00	1,01...11	1.10...00	1,01 ... 11	0,10 ... 00	0,10 ... 00
+0,11...11	1,11...11	1,11...10	1,11...11	1,00 ... 00	0,11 ... 11	0,11 ... 11

Таблиця 1. 3. Коди з доповненням

Число	DD 1	DD 2	DD 3	DD 4	DZ 2	DZ 1
-0,11... 11	1,11 ... 11	1,11 ... 10	1,11 ... 11	1,00 ... 00	0,11 ... 11	0,11 ... 11
-0,10... 00	1.10 ... 00	1,01 ... 11	1,10 ... 00	1,01 ... 11	0,10 ... 00	0,10 ... 00
-0,01... 11	1,01 ... 11	1,01 ... 10	1.01 ... 11	1,10 ... 00	0,01 ... 11	0,01 ... 11
-0,00... 01	1,00 ... 01	1,00 ... 00	1,00 ... 01	1,11 ... 10	0.00 ... 01	0.00 ... 01
-0,00... 00	1,00 ... 00	0,11 ... 11	1,00 ... 00	1,11 ... 11	0,00 ... 00	0,00 ... 00
+0,00... 00	1,00 ... 00	0,11 ... 11	0,11 ... 11	1,11 ... 11	1,11 ... 11	0,00 ... 00
+0,00... 01	0,11 ... 11	0,11 ... 10	0,11 ... 10	0,00 ... 00	1,11 ... 10	1,11 ... 11
+0,01... 11	0,10 ... 01	0,10 ... 00	0,10 ... 00	0,01 ... 10	1,10 ... 00	1.10 ... 01
+0,10... 00	0,10 ... 01	0,01 ... 11	0,01 ... 11	0,01 ... 11	1,01 ... 11	1,10 ... 00
+0,11... 11	0.00 ... 01	0,00 ... 00	0,00 ... 00	0,11 ... 10	1,00 ... 00	1,00 ... 01

Таблиця 1. 4. Комбіновані коди

Число	ZD	CZ	DC 1	DC 2
- 0,11 ... 11	1,11 ... 11	0,11 ... 11	0,00 ... 00	1,00 ... 00
- 0,10 ... 00	1,10 ... 00	0,10 ... 00	0,11 ... 11	1,01 ... 11
- 0,01 ... 11	1,01 ... 11	0,01 ... 11	0,10 ... 00	1,10 ... 00
- 0,00 ... 01	1,00 ... 01	0,00 ... 01	0,11 ... 10	1,11 ... 10
- 0,00 ... 00	1,00 ... 00	0,00 ... 00	0,11 ... 11	1,11 ... 11
+0,00 ... 00	0,00 ... 00	1,00 ... 00	1,11 ... 11	0,11 ... 11
+0,00 ... 01	0.00 ... 01	1,00 ... 01	1,11 ... 10	0,11 ... 10
+0,01 ... 11	0,01 ... 11	1,01 ... 11	1,10 ... 00	1,10 ... 00
+0,10 ... 00	0,10 ... 00	1,10 ... 00	1,10 ... 11	0,01 ... 11
+0,11 ... 11	0,11 ... 11	1,11 ... 11	1,00 ... 00	0,00 ... 00

У табл. 1.1 дано найменування відомих кодів у вітчизняній і зарубіжній термінології. Зазначимо, що з шістнадцяти можливих знакозмінних двійкових кодів до теперішнього часу згадувалися лише 10.

Традиційними кодами є прямий ( ZD), зворотний () і додатковий . Зворотний код відрізняється від додаткового вибором іншого значення зсуву   у від’ємній області. Коди ,і  мають інверсний знак. Слід зазначити, що код , який часто називають зсунутим, використовується в ЄС ЕОМ для представлення порядку чисел і в інтегральних цифро-аналогових перетворювачах при організації біполярного режиму роботи.

Отримані коди розділимо на три групи.

1. Коди, родинні прямому ( , , , ). Ця група характеризується тим, що коди додатніх і від’ємних чисел відрізняються тільки значенням знакового розряду. В цих кодах легко виконуються операції зміни знаку числа (інвертування знакового розряду), кодування і декодування чисел, множення і ділення. Недолік таких кодів: неможливість заміни операції віднімання додаванням.

2. Коди, родинні зворотному (, , , ). У цій групі коди додатніх і від’ємних чисел взаємно інверсні, причому цифрові розряди в одній з областей збігаються з оригіналом. В цих кодах зручно виконувати операції зміни знаку числа, кодування і декодування, алгебраїчного додавання. До недоліків відноситься необхідність реалізації циклічного переносу, складність корекції при множенні.

3. Коди, родинні додатковому (, , , , , , , ). Такі коди відрізняються від зворотних кодів одиницею МЗР в одній з областей і характеризуються простотою виконання операції алгебраїчного додавання, але разом з тим утруднені операції зміни знаку, кодування, декодування і множення.

Існування головного переходу поблизу нуля, тобто одночасне зміна цифр у всіх двійкових розрядах при переході через нуль, - загальний недолік кодів, родинних зворотного і додаткового, який обумовлює небажані викиди на виході біполярного ЦАП.

Іншим недоліком, одночасно властивим кодами, родинним прямому і зворотному, є неоднозначність представлення нуля, однак для кодів першої групи відміну є тільки в знаковому розряді. Тому використання в ЦАП і АЦП кодів, родинних прямим, дозволяє одержати більш високу точність перетворення при малих рівнях аналогового сигналу (поблизу нуля).

Як відомо, для додаткового коду розроблені алгоритми множення і ділення, які не потребують введення корекції. Очевидно, що аналогічні алгоритми можна використовувати при виконанні цих операцій в коді , Який представляє собою додатковий код з інверсним знаком (таблиця 1.2).

В ненадлишкових системах числення величини зміщення і доповнення можуть бути рівними - , 0, ,,,. У надлишкових системах числення вибір значень зміщення і доповнення більш широкий. Так, наприклад, в двійково-десятковій системі числення 8421 існує безліч   кодів, в яких величина зміщення негативній області С ₂ може приймати наступні значення (таблиця 1.5):

,

,

(Інверсний код),

 (Додатковий код),

 (Код з потетрадного доповненням до 16).

Таблиця 1. 5. Деякі знакозмінні двійково-десяткові коди системи числення 8421

Тип коду	Позначення коду	Величина зсуву та доповнення	Найменування коду
С	СС 5		Зміщений інверсний
	СС 8		Самодоповнювальний інверсний (з надлишком 3)
	ZC 3		Інверсний
	ZC 5		З потетрадним доповненням до 16
D	DD 5		, Крім знака
	DD 8		, Крім знака
	DZ 3
	DZ 5		З потетрадним доповненням до 16 коду

У таблиці 1.5 не внесені коди, аналогічні відповідними кодами ненадлишкових систем числення таблиця 1.1, наприклад коди , та ін. Операція зміни знака в цих кодах вимагає не двійкової інверсії, а потетрадного доповнення до 9. З кодів, зазначених *, можна отримати коди, родинні додатковим, збільшенням   на

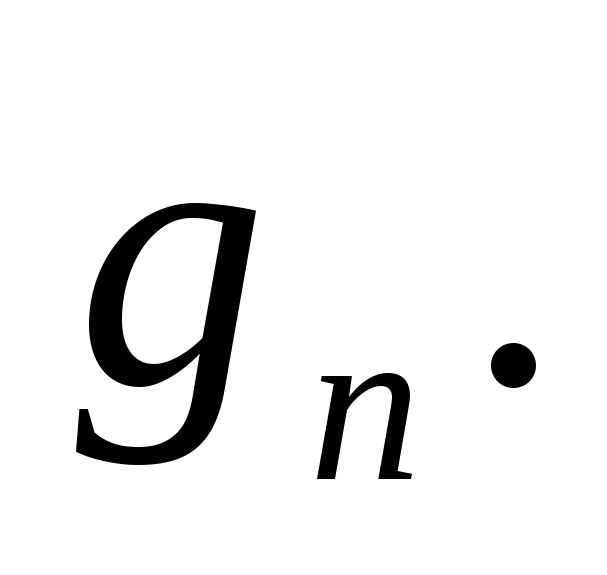
З перерахованих ZC  кодів найчастіше застосовуються перші два, так як вони пов'язані з традиційними правилами отримання зворотних і додаткових кодів в десяткових системах числення. Як відомо, в ЄС ЕОМ при виконанні операції додавання двійково-десяткових чисел з різними знаками застосовується код

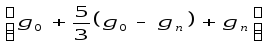
Розглянемо деякі CC-коди двійково-десяткових систем числення. Так, наприклад, у системі числення 8421 вибір зміщення в додатній області   можливий в межах від   до , а у від'ємній області  - від до .

Для спрощення операції зміни знаку числа зручно користуватися так званими інверсними кодами, в яких коди від'ємних чисел виходять з кодів додатніх чисел заміною нулів одиницями і одиниць нулями у всіх розрядах, включаючи знаковий.

Необхідна умова існування інверсного коду системи числення 8421 має вигляд

.

В будь-який іншій двійково-десятковій системі числення, що має вагу розрядів -й тетради ,,,інверсний код отримаємо, якщо при виборі величин зміщень и  задовольняється співвідношення

.

(1.11)

Реалізація алгоритмів десяткової арифметики спрощується при використанні так званих самодоповнювальних кодів, тобто таких кодів, в яких заміна в числових розрядах нулів одиницями і одиниць нулями перетворює число X  в число .

Природно, що самодоповнювальні (з доповненням до 9 в кожній тетраді) коди двійково-десяткових систем, в яких , виходять при виборі величини зміщення додатній області , наприклад відомі самодоповнювальні коди систем числення 2421, 3321,   і т.п.

В будь-якій іншій системі числення, коли , самодоповнювальний код виходить при певному виборі зміщення позитивній області . Якщо сума ваг такої системи числення непарна, величину зміщення позитивній області вибирають за формулою

.

(1.12)

 Так, наприклад, у системі числення 8421, що має , Самодоповнювальний код отриманий при виборі величини зміщення позитивній області .

Цей код називають кодом 8421 + 3, або з надлишком 3. Інверсний код з надлишком 3 виходить при виборі величини зміщення .

Як відомо, код з надлишком 3, що представляє собою зміщений код системи числення 8421, до теперішнього часу відносили до класу «невиважених» кодів систем числення, в яких ваги окремих розрядів мають «змінна» значення.

Система числення 6421 має суму ваг . Якщо в цій системі числення вибрати і, Отримаємо самодоповнювальний інверсний код 6421 + 2 (з надлишком 2). Аналогічно, в системі числення 4421 є самодоповнювальний інверсний код 4421 + 1 (з надлишком 1).

Якщо сума ваг парна, можна в такій системі побудувати самодоповнювальний код з доповненням до 9 в кожній тетраді, в якому заміна в числових розрядах нулів одиницями і одиниць нулями перетворює число X  в число , якщо величину зміщення позитивній області   вибрати рівною

.

(1.13)

 Аналогічно серед групи D-кодів двійково-десяткових систем числення можуть бути знайдені самодоповнювальні. Якщо сума ваг системи числення дорівнює 9, самодоповнювальний код в такій системі числення отримуємо при виборі величини зміщення

.

Якщо   непарна, самодоповнювавльнийя код виходить при виборі величини зміщення

.

(1.14)

Наприклад, у системі числення 8421 самодоповнювальний код виходить, якщо вибрати величину зміщення , а в системі числення 6421 - при .

У розвиток викладеного відзначимо, що система числення 2421 може бути інтерпретована як один з кодів системи числення 8421, в якому додатня область розбивається на дві частини, для кожної з яких вибирається своя величина зсуву: ,. При такому підході умова отримання інверсних кодів зберігається, якщо замість  і  у вираз (1.11) підставляти ідля  Систему числення 6421 можна розглядати як один з кодів системи числення 8421, у якого ,.

Сформульовані правила отримання самодоповнювальних й інверсних кодів значно розширюють наші уявлення про принципи кодування знакозмінної двійково-десяткового інформації, дозволяють встановити взаємозв'язок між різними кодами двійково-десяткових систем числення, спрощують знаходження формул декодування, якими зручно користуватися при синтезі біполярних цифро-аналогових перетворювачів. Так, наприклад, код з надлишком 3 являє собою -код системи числення 8421, завдяки чому були знайдені математичні вирази, що описують операцію декодування, з використанням яких були побудовані декодуючі сітки й перетворювачі коду 8421 + 3 в пропорційне напругу.

Розглянемо систему залишкового класу, в якому основи - 7,5,3.

Q = p ₃ p ₂ p ₁ = 105

Додавання виконується без переносів

Переклад з СЧ залишкових класів в класичну позиційну СЧ.

1. метод ортогональних базисів

Для представлення негативних чисел можна використовувати також і двійкову систему числення, в якій спеціальний знаковий розряд відсутній. У такій системі числення підставу p = -2, у зв'язку з чим така система називається мінус двійковій СЧ. За допомогою чотирьох двійкових розрядів у звичайній системі можна представити числа від 0 до 15, в мінус двійковій системі - числа від -10 до +5.

У цій системі числення позитивне число буде мати в старшому парному розряді одиницю. Від’ємнне число буде мати одиницю в старшому непарному розряді. Так як вага переносу зі i-го розряду в сусідній, старший розряд має зворотний знак, то він реалізується таким чином: якщо в старшому розряді в результаті складання виходить 1, то вона цим перенесенням гаситься (змінюється на нуль), якщо ж у старшому розряді виявився 0, то таке перенесення роздвоюється: додається одиниця в старший і наступний за ним розряди.