1.4.2.Загальні принципи побудови систем з послідовним обчисленням символів

Побудова систем числення класу А, які прийнято називати позиційними ППС, починають з вибору допустимого для кожної позиції кількості символів , формування алфавіту А і обчислення кількісних мір , Які називаються в цьому випадку вагами розрядів, тобто знаходження базису . Таким чином, для позиційних систем числення первинними параметрами є базис (Набір всіх мір ), Допустиме для кожної позиції кількість символів та алфавіт А.

У системах числення, в яких і , для задоволення вимог забезпечення безперервності подання величин ваги наступних розрядів повинні вибиратися, виходячи з наступної умови:

  _.

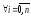Вибравши ваги, розраховують основи, що характеризують кожну позицію по формулі:

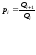
Приклад. 22  2 mod 5   22  1 mod 7   X = [x / p] p + a   X = a mod p

Якщо всі кількісні міри, що входять в базис, рівні між собою, тобто , Отримуємо непозиційної систему числення МПС, яка виступає як окремий випадок позиційної системи. У цих системах числення всі осноави . Як приклад розглянемо непозиційну систему числення, звану унарна або одинична, в якій для запису числа застосовується лише один символ. У цій системі всі , , , , , , . До цього ж класу відносять і "римську" систему числення, в якій для позначення чисел 1, 5, 10, 50, 100, 500, 1000 використовуються великі літери I, V, X, ..., C, D, M. В "римської" системі   при   і   при   тобто .

Особливість позиційних систем полягає в тому, що в них базис обов'язково включає не всі рівні між собою кількісні міри (ваги). Систему числення, в якій вага кожного наступного розряду не менше, ніж ваги всіх попередніх розрядів, будемо називати впорядкованою. Очевидно, що в упорядкованих системах числення обов'язково всі основи .

Позиційна система числення, в якій основи всіх розрядів виявилися однаковими тобто   для всіх   називається однорідною.

В однорідній системі числення, що має , вага   - розряду обчислюється за формулою .

У зв'язку з тим, що в однорідній системі використовується тільки одна основа, зручно таку систему називати за значенням її заснування. Наприклад, систему числення з основою   - двійкова, з основою   - трійкова і т.д. Якщо в позиційній системі числення ваги вибрані таким чином, що не всі основи виявилися однаковими, отримують систему числення яку прийнято називати неоднорідною. У неоднорідною системі числення вага -розряду пов'язаний з основами всіх попередніх розрядів наступним співвідношенням:

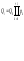
До неоднорідних систем числення, що мають цілочисельні основи, можна віднести систему виміру часу, систему числення, в якій в якості основи обраний набір взаємно простих чисел.

У позиційних системах як однорідних, так і неоднорідних, можуть використовуватися не тільки цілі, але дробові й ірраціональні основи. Так, наприклад, відомі, приклади використання однорідних систем числення з дробовими основами, рівними , де   - може вибратися, рівним 2, 3 і т.д., ірраціональним основою   для з основою , Що дорівнює числу "золотої" S-пропорції, визначається виразом , де   - -е   - Число Фібоначчі.

У так званої факторіальної системи числення, в якій ваги , всі основи являють собою також цілі числа, так як   для всіх .

Можна навести велику кількість прикладів неоднорідних систем числення з ірраціональною основою. Наприклад, система числення, в якій ваги представляють собою ряд послідовних натуральних чисел, тобто , має основи, рівні

.

Система числення, в якій вага молодшого розряду , , а ваги інших розрядів - парні числа, має основу   для .

Система числення, в якій ваги   дорівнюють числам Фібоначчі, тобто

, Де

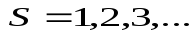
Тоді

Якщо вибрано , Ваги розрядів такої неоднорідної системи виявляються рівними 1, 2, 3, 5, 8, 13, і т.д., якщо вибрано , Ваги розрядів відповідно рівні 1, 1, 2, 3, 4, 6, 9, 13 і т.д.

Якщо базис позиційної системи числення знайдений, можна визначити в якій кількості присутня кожна з обраних мір , Починаючи з найбільшої з ваг   В результаті першого поділу отримуємо частку   і залишок :

, де .

Потім ділимо залишок   на наступну вагу

, де 0 ≤ r _{n - 1} ≤ Q _{n + 1}

або .

Далі залишок   ділимо на   і т.д. Процес поділу продовжуємо до тих пір, поки не буде знайдений останній залишок . В результаті такого поділу отримали представлення числа   у вигляді послідовності символів , починаючи зі старшого символу . Неважко переконатися в тому, що виконуючи послідовний поділ вихідного числа   утворюється в результаті поділу часток на основу , починаючи з основи   можна визначити символи , починаючи з молодшого символу .

Зауважимо, що в кожному розряді кількість цілочисельних значень   залежить від основи даного розряду. Якщо всі   - цілі числа і кількість символів , така система числення є однозначною (не надлишковою), а при цьому  її називають натуральною.

Якщо , при побудові системи числення необхідно обумовлювати, які конкретно символи вибрані для зображення чисел. Системи числення можуть мати не тільки всі додатні цифри, але і всі від'ємні. Система числення з непарною натуральною основою   і цифрами   називаються симетричними. Такі системи числення дозволяють представити будь-яке ціле число, як   додатнє, так і від’ємне. Прикладом симетричної системи числення може служити трійкова система з цифрами [-1,0,1]. Якщо - цілі, а кількість символів   вибрано більшою, ніж _,  тобто , система числення буде неоднозначною. У таких системах числення одна і та ж величина може бути представлена різними послідовностями символів. Наприклад, двійкова система числення з набором символів (-1,0,1). Для дрібних і ірраціональних значень   допустима кількість символів  вибирається з округленням у більшу сторону, тобто   і так як при цьому завжди виявляється, що , Такі системи числення будуть завжди неоднозначними.

Якщо для двох однорідних чисел з основою числення   і   справедливе співвідношення , тоді будемо називати такі числення спорідненими. Так, наприклад, спорідненими будуть двійкова система з чотирковою, вісімковою, шістнадцятковою, чотиркова з шістнадцятковою, а система числення з основами 2 та , основами   і -2, з основами   і 4, з основами -2 і -8 і т.п.

Для неоднорідних систем числення також існує поняття родинних систем при наступномній умові, якщо

для

Слід зазначити, що , де   -   - основа першої системи числення   -   - основа другої системи числення.

Якщо в якійсь системі числення її символи представляються за допомогою цифр іншої системи числення, то таку систему називають системою з кодованим поданням її цифр. Десяткова система числення, в якій кожна десяткова цифра видається тетрадою з двійкових цифр називається двійково-кодованою. Наприклад, так звана двійково-десяткова система числення 8421 являє собою неоднорідну систему числення, у якій використовуються основи і ваги:

і т.д.

 і т.д.

Інша широко поширена двійково-десяткова система числення 2421 являє собою неоднорідну систему числення з основами 2, 2, 0, 5, 5, 2, 2, 0, 5, 5, і т.д. обидві ці системи числення є спорідненими, тому що, за прийнятим визначенням:

Таблиця 1.