golunova_l_v_matematicheskie_modeli_v_transportnyh_raschetah

В таблице хi – i-е значение случайной величины Х; pi – вероятность его появления. При этом ∑ pi = 1.

Эмпирический ряд распределения представляет собой таблицу, в которой перечислены наблюдаемые значения случайной величины и соответствующие им частоты:

В таблице хi – i-я фактическая (наблюдаемая) реализация случайной величины Х; mi – количество появлений (частота) величины хi.

Ряды распределений, образованные из значений случайной величины, характеризующей количественный признак явления (события), называются вариационными.

Биноминальное распределение

Это распределение случайной величины X появления события A в серии из n независимых испытаний. В каждом испытании возможно два исхода: наступление или ненаступление события А. Вероятность наступления события А в каждом испытании – p, а вероятность его отсутствия q = 1 – р. При сформулированных условиях вероятность появления события A опре-

деляется формулой Бернулли:

где Сnm – число сочетаний из n по m.

Эта формула связана с повторением испытаний в одинаковых условиях, в которых как раз и проявляются законы теории вероятности.

Формула (1.23) представляет собой аналитическую форму закона распределения случайной величины, который называется биноминальным: правая часть представляет собой общий член разложения бинома Ньютона. На рисунке 1.1 показаны многоугольники биномиального распределения для некоторых значений величин n и p.

21

p=0,5;n=3

Рисунок 1.1 – Многоугольники биноминального распределения

Пример 1.9. Случайная величина X – число назначений в прибывшем в расформирование составе. С вероятностью p = 0,6 в поезде могут встретиться вагоны на каждое назначение. Определить математическое ожидание, дисперсию, среднее квадратическое отклонение числа назначений в составе, если общее число назначений, на которое станция формирует поезда, равно 15.

Решение:

1. Математическое ожидание числа прибывших вагонов:

М(Х) = n·p = 15·0,6 = 9; 2. Дисперсия: D(X) = n·p·q = 15·0,6·0,4 = 3,6;

3. Среднее квадратическое отклонение: σx = D( X ) = 3,6 ≈ 1,9.

Пример 1.10. В подаче порожних вагонов с вероятностью p = 0,5 каждый из них требует очистки. Определить вероятность того, что в подаче из пяти вагонов очистке будет подвергнуто 0, 1, 2, 3, 4 или все пять вагонов.

Решение:

Заметим, что p = 0,5; q = 1 – 0,5 = 0,5. Тогда имеет место равенст-

во pmqn−m = pm+(n−m) = pn , или Pn(m) = Сnm pn .

Отсюда вероятность того, что ни один вагон не требует очистки:

P5(0) = С50 p5 = 1·0,55 = 0,03125.

P5(3) = 0,3125; P5(4) = 0,15625; P5(5) = 0,03125.

5

Проверка: ∑P(i ) =1,0.

i =0

Распределение Пуассона

Данное распределение является предельным случаем би-

22

номиального распределения. Пусть в каждом из n проводимых испытаний вероятность появления события A равна p. Предположим, что p → 0 и n → ∞ так, что n·p → M(Х) = а > 0 является постоянной величиной. Тогда вероятность наступления события A задается формулой:

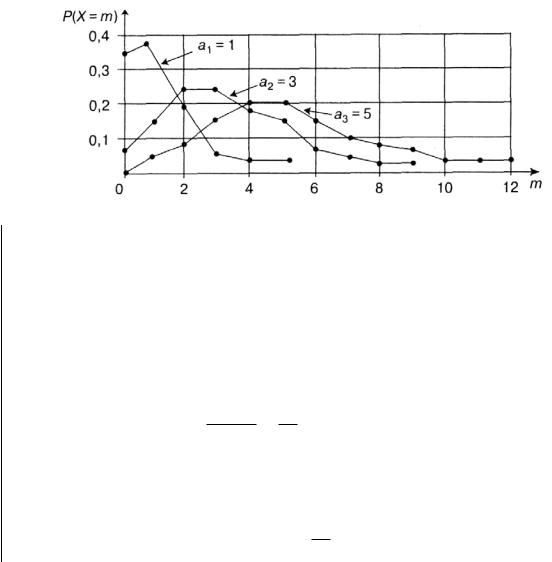
Формула (1.24) представляет собой закон распределения Пуассона. На рисунке 1.2 показаны графики распределения Пуассона, отвечающие различным значениям математического ожидания. При увеличении математического ожидания кривые распределения Пуассона становятся более симметричными. При а ≥ 10 кривые становятся практически симметричными, и закон Пуассона можно заменять нормальным законом распределения с определенными допущениями.

Рисунок 1.2 – Графики распределения Пуассона

Пример 1.11. В парк приема станции прибывает ежесуточно 1500 вагонов. Вероятность нахождения среди них неисправного вагона равна 0,002. Определить вероятность того, что в данные сутки будет обнаружено более одного неисправного вагона.

Решение:

1.Математическое ожидание числа неисправных вагонов в сутки:

а= n·p = 1500·0,002 = 3

2.Вероятность обнаружения одного неисправного вагона:

P(1) = ame−a = a1 e−a = 3e−3 = 0,149 . m! 1!

3. Вероятность того, что на станции будет обнаружен хотя бы один неисправный вагон, равна вероятности того, что на станции будет обнаружено не менее одного неисправного вагона:

P(X≥1) = 1 – P(0) =1− a0 e−a =1−e−3 = 0,95 .

0!

23

1.2.2.Непрерывные случайные величины

1.2.2.1.Функция и плотность распределения вероятности

Пусть X – непрерывная случайная величина, значения которой сплошь заполняют некоторый интервал. При этом каждое отдельное значение обычно не обладает никакой отличной от нуля вероятностью. Поэтому необходима характеристика распределения вероятности, применимая для любых случайных величин. Такая характеристика есть функция распределения.

Функцией распределения случайной величины X называ-

ется функция F(x), определяющая вероятность того, что случайная величина X примет любое значение, меньшее x (X <x),

24

Плотность распределения f(x) есть предел отношения ве-

роятности попадания случайной величины на малый участок и длины этого участка при ее неограниченном уменьшении.

Вероятность попадания случайной величины на произвольный участок [а, b) равна:

a

Интеграл в бесконечных пределах от плотности распреде-

ления равен единице, то есть +∞∫ f(x) dx = 1. Это очевидно, так

−∞

как указанный интеграл выражает вероятность достоверного события – попадания случайной величины на участок от –∞ до ∞, а значит, равен единице.

График

25

1.2.2.2. Числовые характеристики непрерывных случайных величин

Определения числовых характеристик дискретных случайных величин распространяются и на непрерывные величины. Разница состоит в том, что вместо сумм в формулах (1.17) и (1.19) берутся их интегральные аналоги. Формулы для математического ожидания и дисперсии:

D(X) = ∫b (x – M(X))2 f(x) dx.

a

Среднее квадратическое отклонение непрерывной случайной величины определяется по формуле (1.20):

σx = D(X ) .

Для вычисления дисперсии употребляется более удобная

Пример 1.12. Случайная величина задана плотностью распределения:

Определить математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X.

Решение:

1. Математическое ожидание:

2. Дисперсия и среднее квадратическое отклонение:

1.2.2.3. Основные распределения непрерывных случайных величин

Равномерное распределение

В некоторых транспортных задачах встречаются непрерывные случайные величины, расположенные в некотором интервале с равной вероятностью.

26

Распределение вероятностей называется равномерным, если на интервале возможных значений случайной величины плотность распределения является постоянной.

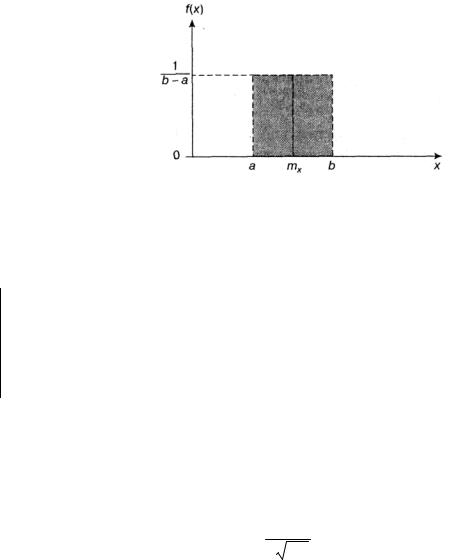
График плотности равномерного распределения (1.33) показан на рисунке 1.4.

Рисунок 1.4 – График плотности равномерного распределения

Вероятность попадания равномерно распределенной слу-

Пример 1.13. Порожние вагоны поступают к пункту погрузки через 4 часа. Какова вероятность того, что время погрузки не превысит 3 часа?

Решение:

Так как (β – α) = 3 часа, (b – a) = 4 часа, то P(0 < X < 3) =3/4 = 0,75.

Нормальное распределение

Общим нормальным распределением вероятностей непре-

рывной случайной величины X называется распределение с плотностью

График плотности нормального распределения (1.35) для разных значений σ показан на рисунке 1.5.

Нормальное распределение задается двумя параметрами: а и σ. После выполнения соответствующих интегрирований можно вывести, что для нормального распределения справедливы формулы:

27

3. По приложению А определим значение стандартной нормальной функции распределения:

Ф(z2) = Ф(1,24) = 0,892; Ф(z1) = Ф(–1,24) = 0,107.

4. Вероятность окончания разгрузки вагона в течение интервала времени [1,5; 2,5] будет равна:

p(1,5 < t < 2,5) = Ф(z2) – Ф(z1) = 0,892 – 0,107 = 0,785.

Показательное распределение

Непрерывная случайная величина X имеет показательное распределение, если ее плотность распределения выражается формулой:

x – текущее значение исследуемой величины. Положительная величина X является параметром показа-

тельного распределения. Функция распределения случайной

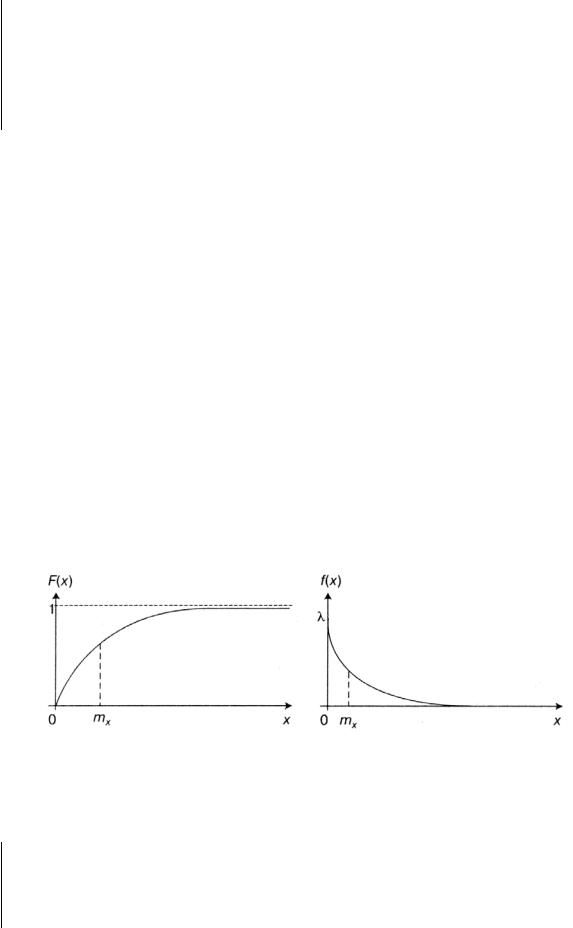
Графики функции и плотности показательного распределения приведены на рисунке 1.6. Математическое ожидание и дисперсия случайной величины X:

Рисунок 1.6 – График функции и плотности показательного распределения

Пример 1.15. Математическое ожидание числа выходов из строя радиостанций у составителей поездов за 10000 часов работы равно 10. Определить вероятность выхода из строя радиостанций за 1000 часов работы.

29

Решение:

1. Интенсивность выхода из строя радиостанций за 1 час:

λ = 10/10000 = 0,001.

2. Вероятность выхода из строя за 1000 часов: P(t ≤ 1000) =

F(t = 1000) = 1– e–0,001·1000 = 1 – e–1,0 = 1 – 0,3679 = 0,6321.

1.3. ОСНОВЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ

Математическая статистика охватывает ряд вопросов, относящихся к характеру проявления закономерностей в массовых процессах и к способам их наблюдения и констатации. Первая задача математической статистики состоит в указании методов сбора и группировки статистических сведений, которые получены в результате экспериментов или наблюдений. Вторая задача – это разработка методов анализа статистических данных: оценки неизвестных вероятности события, а также функций и параметров распределения; оценки зависимости случайной величины от других случайных величин; проверки статистических гипотез о виде и величинах параметров неизвестного происхождения.

Последовательность статистического исследования обычно следующая: наблюдения, группировка и сводка результатов наблюдений; определение числовых характеристик статистического распределения; построение статистического ряда и гистограммы; подборка теоретической кривой; проверка выдвинутой гипотезы по критерию согласию.

Эмпирические ряды распределения, получаемые при обработке первичных статистических данных, оформляются в таблицах или изображаются графически. Построение эмпирических графиков и диаграмм позволяет установить на первом этапе исследования, к какому типу теоретического распределения ближе всего полученное эмпирическое распределение, что облегчает выбор конкретных технических приемов обработки исходных данных. Для применения графического метода анализа распределений необходимо знать, как строить графики распределения, какие существуют типы распределений и какими свойствами обладают теоретические распределения.

Рассмотрим, как производится обработка статистического материала. При функционировании какой-либо системы или её элемента в течение некоторого времени t случайная величина X

30