
golunova_l_v_matematicheskie_modeli_v_transportnyh_raschetah
.pdf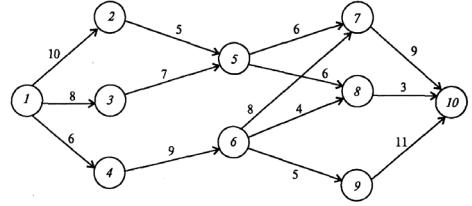
ре. Пусть сеть состоит из 10 узлов (городов), соединенных магистралями согласно схеме (рисунок 6.1).
Рисунок 6.1 – Транспортная сеть
Стоимость проезда из i-го пункта в j-й пункт равна tij (значения tij показаны на схеме). Требуется найти оптимальный маршрут из 1-го пункта в 10-й.
В данной задаче имеется серьезное ограничение: двигаться по магистралям можно только слева направо. Поэтому разобьем всю транспортную сеть на пояса и отнесем каждый из десяти пунктов к одному из четырех поясов. Пункт принадлежит k-му поясу, если из него можно попасть в конечный (10-й) пункт ровно за k шагов, то есть с заездом ровно в k–1 промежуточный пункт. Таким образом, пункты 7, 8 и 9 принадлежат к первому поясу, 5 и 6 – ко второму, 2, 3 и 4 – к третьему и 1 – к четвертому. На k-м шаге будем находить оптимальные маршруты из городов k-го пояса до конечного пункта.
Оптимизацию будем производить с хвоста процесса, поэтому, добравшись до k-го шага, мы не можем знать, в какой именно из городов k-го пояса мы попадем, двигаясь из пункта 1. Для каждого из этих городов мы должны будем найти оптимальный маршрут до конечного пункта. Очевидно, что минимально возможная стоимость проезда из городов k-го пояса до пункта 10 будет зависеть только от того, в каком из городов этого пояса мы оказались. Номер S города, принадлежащего k- му поясу, будет называться переменной состояния данной системы на k-м шаге. Следует помнить, что, добравшись до k-го шага, мы уже осуществили предыдущие шаги, то есть нашли оптимальные маршруты по перемещению из любого города (k–
161
1)-го пояса в конечный пункт. Таким образом, находясь в некотором городе S k-го пояса, мы должны решить, в какой из городов (k–1)-го пояса следует отправиться, а направление движения уже понятно из предыдущих шагов. Номер J города (k–1)- го пояса будет являться переменной управления на k-м шаге.
Функция Беллмана на k-м шаге решения задачи дает нам возможность рассчитать минимальную стоимость проезда из города S k-го пояса до конечного пункта. Для первого шага (k=1) – это стоимость проезда из городов 1-го пояса непосредственно до конечного пункта: F1(i) = Ci10. Для последующих шагов стоимость проезда складывается из двух слагаемых: стоимости проезда из города S k-го пояса в город J (k–1)-го пояса и минимально возможной стоимости проезда из города J до конечного пункта, то есть Fk–l(J). Таким образом, функциональное уравнение Беллмана на k-м шаге решения будет иметь вид:
Fk(S) = minj {tsj + Fk–1(j)}.
Минимум стоимости достигается на некотором значении J*, которое и является оптимальным направлением движения из пункта S в сторону конечного пункта.
На четвертом шаге мы попадаем в 4-й пояс, и состояние системы становится определенным S = 1. Функция Беллмана F4(1) представляет собой минимально возможные затраты по перемещению из 1-го пункта в 10-й. Оптимальный маршрут можно найти, просмотрев результаты всех шагов в обратном порядке, учитывая, что выбор некоторого управления J на k-м шаге приводит к тому, что состояние системы на (k–1)-м шаге становится определенным.
I этап. Условная оптимизация
1-й шаг. k = 1. F1(S) = tS10.
S |
J=10 |
F1(S) |
J* |
1 |
9 |
9 |
10 |
8 |
3 |
3 |
10 |
9 |
11 |
11 |
10 |
2-й шаг. k = 2. Функциональное уравнение на данном шаге:
162
F2(S) = minj {tsj + F1(j)}.
Результаты расчета приведены ниже:
S |
J=7 |
J=8 |
J=9 |
F2(S) |
J* |
5 |
6 + 9 |
6 + 3 |
– |
9 |
8 |
6 |
8 + 9 |
4 + 3 |
5 + 11 |
7 |
8 |
3-й шаг. k = 3. Функциональное уравнение на данном шаге:
F3(S) = minj {tsj + F2(j)}.
Результаты расчета приведены ниже:
S |
J=5 |
J=6 |
F3(S) |
J* |
2 |
5 + 9 |
– |
14 |
5 |
3 |
7 + 9 |
– |
16 |
5 |
4 |
– |
9 + 7 |
16 |
6 |
4-й шаг. k = 4. Функциональное уравнение на данном шаге:
F4(S) = minj {tsj + F3(j)}.
Результаты расчета приведены ниже:
S |
J=2 |
J=3 |
J=4 |
F4(S) |
J* |
1 |
10 + 14 |
8 + 16 |
6 + 16 |
22 |
4 |
II этап. Безусловная оптимизация
На этапе условной оптимизации получено, что минимальные затраты на проезд из пункта 1 в пункт 10 составляют F4(1) = 22, что достигается движением по следующим магистралям. Из пункта 1 следует направиться в пункт 4, затем в пункт 6, далее в пункт 8 и из него в пункт 10. Таким образом, оптимальный маршрут будет 1–4–6–8–10.
Таким образом, при динамическом подходе к решению задачи стремятся найти не изолированные оптимальные решения для отдельных расчетных моментов, а общий оптимум, дающий минимальные издержки для всей задачи.
6.3. ПРИМЕРЫ ЗАДАЧ
На железнодорожном транспорте помимо рассмотренной задачи о кратчайшем пути на сети дорог метод динамического программирования решают ещё целый ряд задач.
В задаче о режиме ведения поезда необходимо определить
163
такой режим ведения поезда на любом отрезке пути, который обеспечил бы минимальные приведенные расходы на передвижение по участку в целом. Расходы на каждом отрезке пути зависят от скорости поезда и от сопротивления движению, а последнее – от профиля пути. Поэтому в качестве вычислительного этапа рассматривается элемент профиля пути с постоянным уклоном.
Другая задача – оптимизация развития пропускной спо-
собности линии. Усиление пропускной способности можно осуществить различными способами: устройством автоблокировки и диспетчерской централизации, удлинением станционных приемо-отправочных путей, укладкой двухпутных вставок для организации безостановочных скрещений поездов, вторых путей, использованием более мощных локомотивов и др. Каждый из этих способов требует определенных капитальных вложений. Затраты какого-либо способа усиления пропускной способности позволяют поднять ее уровень до определённой величины. Затем необходимо изыскать другой способ, который также потребует капитальных вложений в определенный срок и т. д. Во многих случаях величину капитальных вложений определяет прирост грузопотока, который необходимо освоить. Например, мощность новых локомотивов должна быть тем больше, чем больше прирост грузопотока, который подлежит освоению ими, удлинение приемо-отправочных путей также зависит от величины дополнительного грузопотока, который необходимо освоить. Чем больше мощность локомотивов, или величина удлинения приемо-отправочных путей, тем больше и капитальные вложения на усиление пропускной способности тем или иным способом. С известной степенью условности можно считать, что величина капитальных вложений пропорциональна приросту грузопотока, а последний – времени эксплуатации линии в результате усиления пропускной способности данным способом.
При решении задачи предполагают, что на рассматриваемой линии, например, можно использовать три способа усиления пропускной способности в определенной последовательности на протяжении нескольких лет. Каждый из этих способов позволяет освоить различные размеры дополнительного грузо-
164
потока в зависимости от величины капитальных затрат. Необходимо определить размеры и сроки вложения капитальных затрат, чтобы общие расходы на усиление пропускной способности всеми тремя способами были минимальными. При этом необходимо учесть экономический эффект от отдаления капитальных вложений, приводя их к начальному году периода.
Рассмотренные задачи динамического программирования показывают суть метода: пошаговая оптимизация, проходимая в одном направлении условно, в другом – безусловно. В отличие от линейного программирования динамическое программирование не сводится к стандартной вычислительной процедуре. Достоинством метода динамического программирования является то, что при выборе управления на каком-либо шаге для состояния S рассматриваются не все возможные продолжения, а только те, которые соответствуют оптимальным продолжениям. Такой подход позволяет исключить из рассмотрения огромное количество не представляющих интереса вариантов.
Среди недостатков следует отметить тот факт, что до самого последнего момента остается неизвестным, каково же будет оптимальное управление для заданного начального состояния. При этом оказывается, что большая часть вычислений была проделана напрасно, так как результаты определения оптимального управления для состояний, не лежащих на оптимальной траектории, не используются.
6.4. РЕШЕНИЕ ЗАДАЧ ДИНАМИЧЕСКОГО ПРОГРАММИРОВА- НИЯ СРЕДСТВАМИ MS EXCEL
Пусть дана некая транспортная сеть (трубопровод, железная дорога и др.), по которой мы хотим перемещать некоторые однородные единицы (машины, нефть и др.) из одной точки сети (пункта отправления) в другую (пункт назначения) – рисунок 6.2. Также сеть включает в себя промежуточные узловые пункты, соединенные между собой и с первыми двумя. Узловые пункты при этом можно интерпретировать как развилки транспортных путей. Обозначим пункт отправления цифрой 0, пункт назначения – буквой m, а узловые пункты – их порядковыми номерами, тогда общее количество узлов может быть от 0 до m. Условимся в общем случае обозначать путь, связываю-
165
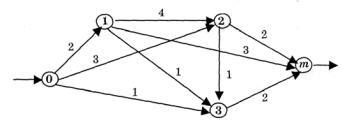
щий узловые пункты, записью (i, j). Связи такой сети, являются направленными, то есть поток грузов вдоль каждого из этих путей происходит в направлении, указанном стрелкой. Причем их пропускная способность ограничена (например, трубопровод может пропускать только определенное количество нефти в час и т. п.). Обозначим максимальную пропускную способность каждого из путей как fij. Например, на рисунке 6.2 максимальный поток f23, пропускаемый путем (2,3), равен 1.
Рисунок 6.2 – Пример транспортной сети
При транспортировке поток грузов следует из пункта 0 по различным путям через узловые пункты в пункт назначения до тех пор, пока все эти грузы не попадут в пункт m. Это означает,
что мы накладываем на сеть условие сохранения потока в про-
межуточных узлах: все, что попадает в такой узел, должно полностью покинуть его.
В качестве примера рассмотрим задачу нахождении крат-
чайшего пути.
Необходимо автотранспортом доставить продукты с оптовой базы в магазины торговой сети, находящиеся на определенной территории. Автомобиль выезжает с оптовой базы, посещает каждый магазин ровно один раз и возвращается назад. Требуется найти маршрут, при котором общая протяженность пути будет минимальной. Пусть необходимо развести товар в пять торговых точек: 1, 2, 3, 4 и 5, расстояния между которыми указаны в таблице 6.1.
|
|
|
|
|
|
Таблица 6.1 |
|
|
|
Исходные данные |
|
|
|
||
|
|
|
|
|
|
|
|
Торговая точка |
1 |
|
2 |
3 |
4 |
|
5 |
1 |
0 |
|
17 |
10 |
15 |
|
17 |
2 |
18 |
|
0 |
6 |
12 |
|
20 |
3 |
12 |
|
5 |
0 |
14 |
|
19 |
4 |
12 |
|
11 |
15 |
0 |
|
7 |
5 |
16 |
|
21 |
18 |
6 |
|
0 |
166
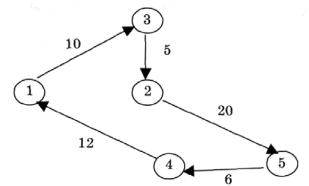
Рассмотрим один из вариантов. Пусть сначала продукты доставляют в магазин 3. Оттуда можно поехать в любой их трех оставшихся магазинов – 2, 4 или 5. Допустим, выбран магазин 2, далее магазин 5, потом 4 и возвращается на оптовую базу. Последовательность такого перемещения можно представить в виде графа (рисунок 6.3), длина пути («обхода») будет равна 10 + 5 + 20 + 6 + 12 = 53. Но кроме этого варианта есть целый ряд других. Для нашего случая (для пяти торговых точек) число таких вариантов составит 24. Поэтому решить задачу простым перебором вариантов даже при незначительном увеличении числа городов становится затруднительно.
Рисунок 6.3 – Один из возможных вариантов маршрута
Введем обозначения. Пусть Xij – путь из i-й точки в j-ю, причем если этот путь используется, то значение Xij = 1, иначе Xij = 0. Так как в соответствии с условием задачи можно посетить каждую точку только один раз, то сумма всех вариантов сочетаний перемещений должна быть равна 1. Тогда, обозначив через Х11, Х12, Х13, Х14, Х15 пути, выходящие из начального
пункта, получим уравнение: Х11 + Х12 + Х13 + Х14 + Х15 = 1. Представим вариант обхода (рисунок 6.3), в виде таблицы
6.2 (нулевые значения обозначают неиспользованные пути).
|
|
|
|
|
Таблица 6.2 |
|
|
|
|
|
|
|
|
Торговая точка |
1 |
2 |
3 |
4 |
|
5 |
1 |
0 |
0 |
1 |
0 |
|
0 |
2 |
0 |
0 |
0 |
0 |
|
1 |
3 |
0 |
1 |
0 |
0 |
|
0 |
4 |
1 |
0 |
0 |
0 |
|
0 |
5 |
0 |
0 |
0 |
1 |
|
0 |
167

Аналогичные уравнения можно составить для других вариантов маршрутов. Для этого видоизменим таблицу исходных данных (таблица 6.3).
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 6.3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Торговая |
|
1 |
|
|
2 |
|
3 |
|
4 |
|
|
5 |
|
точка |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
Х11 |
|
17 |
Х12 |
10 |
Х13 |
15 |
Х14 |
17 |
Х15 |
1 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
||||||
2 |
18 |
Х21 |
0 |
Х22 |
6 |
Х23 |
12 |
Х24 |
20 |
Х25 |
1 |
||
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|||||||
3 |
12 |
Х31 |
5 |
Х32 |
0 |
Х33 |
14 |
Х34 |
19 |
Х35 |
1 |
||
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|||||||
4 |
12 |
Х41 |
11 |
Х42 |
15 |
Х43 |
0 |
Х44 |
|
7 |
Х45 |
1 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
||||||
5 |
16 |
Х51 |
21 |
Х52 |
18 |
Х53 |
6 |
Х54 |
0 |
Х55 |
1 |
||
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|||||||
|
|
1 |
|
|
1 |
|
1 |
|
1 |
|
|
1 |
|
Аналогично запишем ограничения для столбцов: |
|||||||||||||
Х11 + Х21 + Х31 + Х41 + Х51 = 1; |
Х14 + Х24 + Х34 + Х44 + Х54 = 1; |
||||||||||||
Х12 + Х22 + Х32 + Х42 + Х52 = 1; |
Х15 + Х25 + Х35 + Х45 + Х55 = 1. |
||||||||||||
Х13 + Х23 + Х33 + Х43 + Х53 = 1; |
|
|
|
|
|
|
|
||||||
Для исключения образования так называемых «петель» введем также дополнительные ограничения, следующие из условия Xij ≠ Xji:
Х21 + Х12 ≤ 1; |
Х42 + Х24 ≤ 1; |
||||
Х31 |
+ Х13 |
≤ 1; |
Х52 |
+ Х25 |
≤ 1; |
Х41 |
+ Х14 |
≤ 1; |
Х43 |
+ Х34 |
≤ 1; |
Х51 |
+ Х15 |
≤ 1; |
Х53 |
+ Х35 |
≤ 1; |
Х32 |
+ Х23 |
≤ 1; |
Х45 |
+ Х54 |
≤ 1. |
Для поиска наиболее оптимального маршрута необходимо заполнить электронную таблицу так, как показано на рисунке
6.4.Пояснения к ее заполнению приведены в таблице 6.4.
Для нахождения оптимального варианта маршрута исполь-
зуется сервисная надстройка MS Excel Сервис → Поиск решения. Диалоговое окно надстройки показано на рисунке 6.5. Полный перечень ограничений приведен ниже:
$В$11=0; $С$12=0; $D$13=0; $Е$14=0; $F$15=0; $B$11:$F$15≤1; $H$11:$I$15≤1; $B$11:$F$15≥0; $H$11:$I$15≥0; $G$11:$G$15=1; $B$16:$F$16=1; $B$11:$F$15 = целое.
168
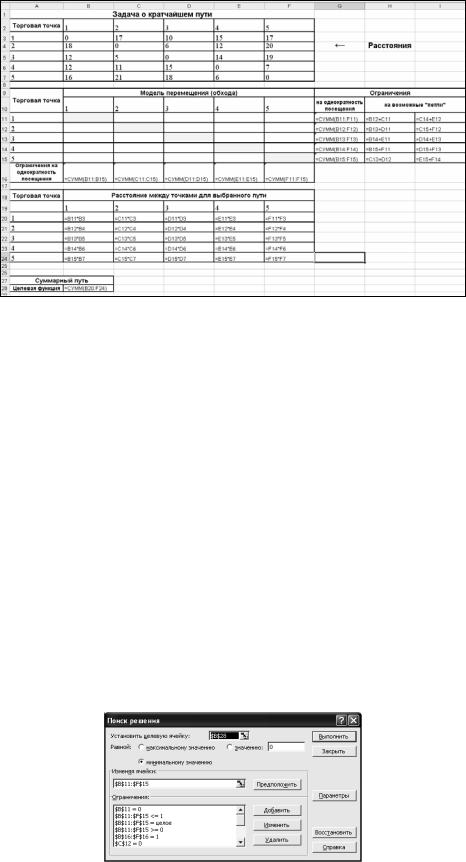
Рисунок 6.4 – Пример заполнения таблицы для решения задачи
|
Таблица 6.4 |
|
|
Адреса ячеек |
Пояснения |
B2:F2, A3:A7, |
Нумерация городов |
B10:F10, B19:F19, |
|
A11:A15, А20:А24 |
|
B3:F7 |
Расстояния между городами (для одного и того же |
|
города на пересечении соответствующих строки и |
|
столбца записывается нулевое значение) |
B11:F15 |
Результат моделирования (Хij) – искомый опти- |
|
мальный путь |
B16:F16 |
Ограничения на однократность посещения (по вер- |
|
тикали) |
G11:G15 |
Ограничения на однократность посещения (по го- |
|
ризонтали) |
Н11:I15 |
Ограничения на «петли» (условие Хij ≠ Xji) |
B20:F24 |
Промежуточные значения для целевой функции |
В27 |
Искомая целевая функция |
Рисунок 6.5 – Диалоговое окно Поиск решения
Полученные результаты расчетов в MS Excel приведены на рисунке 6.6. Таким образом, предлагается оптимальный мар-
169
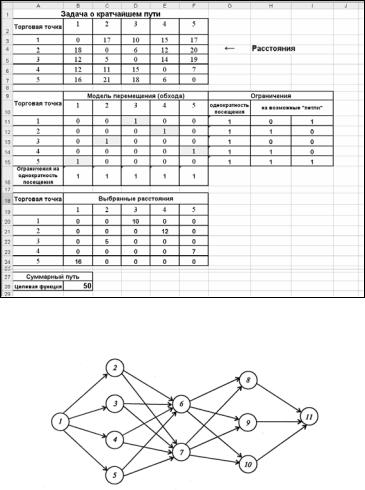
шрут обхода: 1–3–2–4–5–1. При этом суммарная длина пути составит 50 условных единиц.
Рисунок 6.6 – Результат решения задачи о кратчайшем пути
6.5. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
Рисунок 6.7 − Транспортная сеть
В транспортной сети (рисунок 6.7) имеется несколько маршрутов по проезду из начального пункта в конечный пункт. Стоимость проезда между пунктами транспортной сети представлена в таблице (T(i, j)). Необходимо определить оптимальный маршрут проезда из пункта 1 в пункт 11 с минимальными транспортными расходами.
1.
T(1,2) |
T(1,3) |
T(1,4) |
T(1,5) |
T(2,6) |
T(2,7) |
T(3,6) |
T(3,7) |
T(4,6) |
T(4,7) |
T(5,6) |
9 |
10 |
14 |
8 |
7 |
7 |
6 |
5 |
14 |
9 |
12 |
T(5,7) |
T(6,8) |
T(6,9) |
T(6,10) |
T(7,8) |
T(7,9) |
Т(7,10) |
Т(8,11) |
Т(9,11) |
Т(10,11) |
|
10 |
7 |
6 |
4 |
9 |
5 |
11 |
7 |
6 |
10 |
|
2.
T(1,2) |
T(1,3) |
T(1,4) |
T(1,5) |
T(2,6) |
T(2,7) |
T(3,6) |
T(3,7) |
T(4,6) |
T(4,7) |
T(5,6) |
8 |
11 |
13 |
7 |
6 |
8 |
7 |
14 |
13 |
8 |
11 |
T(5,7) |
T(6,8) |
T(6,9) |
T(6,10) |
T(7,8) |
T(7,9) |
Т(7,10) |
Т(8,11) |
Т(9,11) |
Т(10,11) |
|
11 |
9 |
10 |
8 |
7 |
7 |
5 |
3 |
6 |
9 |
|
170
