VI. Додатки

1. Базиси у просторі комплексних функцій

Якщо сукупність 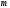комплексних функцій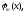заданих на множині дійсних чиселна проміжку, задовольняє умовам

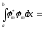
(Д1.1)

то такі функції називаються ортогональними, а умова(Д1.1) - умовою взаємної ортогональності функцій.Функції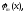називаються базисом або базиснимифункціями, причому простір , як правило, не- скінченний в обох напрямках числової осі. Набірфункцій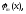можна використати як базис дляпредставлення довільної функції, яка існує уцьому ж просторіx . Її можна однозначно представити лінійною комбінацією функцій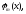 Підпростором можна розуміти часабо Декартів про- стір. Наприклад, положення точки у просторі однозначно задається розкладом радіус-вектора точ ки в одиничних векторах декартових осей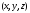 (ортах), проте в чотиривимірному просторі даного базису уже недостатньо.

Розклад у базисі функціонального простору значно спрощує аналіз функції 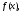, звівши його до аналізу поведінки функцій базису, які, будучи взятими з пев- ними ваговими коефіцієнтами, і формують функцію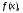. Функція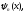, яка розкладається в ряд (або інтеграл) Фур’є, взагалі кажучи, може бути розкладена і за іншим набором базисних функцій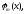що задовольняють умову ортогональності (Д1.1). Якщо існує

дві системи ортонормованих функцiй i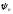(два базиси), то розкладання функції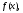може бути виконане за будь-якою із них, причому, між коефіцієнтами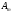,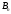цих розкладів можна віднайти зв’язок, використавши рівняння

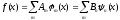(Д1.2)

Помножимо почленно рiвнiсть (Д1.2) на комплексно спряжену

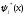i проінтегруємо на проміжку існування базису:

(Д1.3)

Отже, при відомих коефіцієнтах розкладу Аm функцiї у одному із базисів (базисі 1) коефіцієнти її розкладу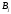в іншому базисі (базисі 2) визначаються за допомогою матриці коефіцієнтів переходу від базису 1 до базису 2.

2. Перетворення Гільберта

Інтегральна операція

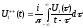(Д2.1)

називається перетворенням Гільберта. При підінтегральний вираз прямує в нескінченність, тому інтеграл слід розуміти як межу:

Зазначимо, що справедливе і обернене перетворення:

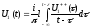(Д2.2)

Уявна частина називається спряженим сигналом. Таким чином, аналітичний сигнал, який відповідає заданому дійсному, одержується простим додаванням спряженого сигналу (Д2.1) до дійсного, тобто, його можна отримувати не лише за правилом (1.118), але і використовуючи спряжений сигнал (Д2.1). Як уже зазначалось, його зміст наочно демонструється на прикладі гармонічних коливань. Приклад. Нехай є дійсне коливанняНа Рис. Д2.1. рис. Д2.1. значення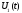відкладаємо вздовж осі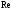. Знаходимо спряжений сиг- нал, виконуючи перетворення Гільберта:

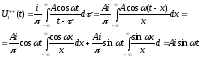(Д2.3)

Тут використана заміна 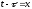, а також значення інтеграліві. Величину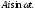відкладаємо вздовж осі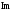. Таким чином, аналітичний сигнал є вектор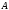, який обертається проти годинникової стрілки із кутовою швидкістю

(Д2.4)

що можна визначити також із рис. Д2.1. Нехай , знайдемо спряжений сигнал. Для цього скористаємося отриманим результатом (Д2.3). Дійсному сигналуу відповідності із (Д2.3) повинен відпо-відати спряжений сигнал

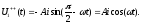(Д2.5)

Аналітичний сигнал при цьому має вигляд:

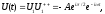(Д2.6)

йому відповідає вектор A , що обертається в комплексній площині за годинниковою стрілкою із швидкістю, і відстає по фазі навідносно значення кута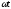. При конструюванні аналітичного сигналу в цьому випадку відбулось занулення області від'ємних частот із всього спектру дійсного сигналу.

В обох розглянутих випадках спряжений сигнал дорівнює по модулю дійсному сигналу і відстає по фазі на 90. Цей результат може бути отриманий безпосередньо застосуванням перетворень Гільберта дофункції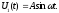

Одержаний аналітичний сигнал репрезентується, як і раніше, вектором довжини | A |, що обертається в комплексній площині з частотою . Тому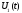є проекція вектора A на дійсну вісь, а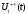є проекцією того ж вектора на уявну вісь. Проекції мають рівні амплітуди, обертаються з однаковою швидкістюз відносною різницею фаз.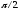

Визначимо спектральну функцію спряженого і комплексного коливань. Хоч відповідь нам по суті уже відома, її корисно отримати, використавши перетворення Гільберта.

За визначенням фур'є-образу

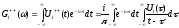(Д2.7)

Введемо нову змінну змінимо порядок інтегрування:

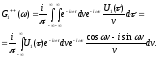(Д2.8)

На рис. Д2.2. показано хід функцій 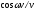і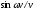 раховуючи асиметрію першої функції, зазначимо, що інтеграл від неї в симетричних межах дорівнює нулю, інтеграл від другої дорівнює та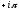для випадків 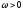i 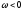відповідно. Оскільки

Рис. Д2.2. Хід функцій 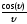та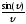

перший інтеграл є фур'є-образ , то

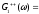
(Д2.9)

Для спектру комплексного сигналу маємо у кінцевому підсумку

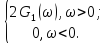(Д2.10)

Останнє співвідношення цікаве тим, що дозволяє одержати комплексний сигнал, застосовуючи ПФ, якщо відомий спектр дійсного сигналу.

3. Фазоконтрастний мікроскоп

Роботу ФКМ, використовуючи метод зон Френеля, можна пояснити наступним чином. Нехай світло паралельним пучком S падає на однорідне середовище із обмеженою апертуроюA, на якому є мала, майже точкова флуктуація показника заломлення, показана на пластинці у вигляді малої областіB. Плоска хвиля S, дійшовши до областіB, частково дифрагує у вигляді сферичної хвиліC. Таким чином, у деяку віддалену точкуD, розташовану на осі, дійдуть дві хвилі: сферична хвиля C′, яка отримає запізнення по фазі завдяки пробігу відстані BD, та плоска S, яка у точціD створює збудженняS′лише половиною центральної зони Френеля, причому фаза його відстає від фази центральної зони (або, що те ж саме, від фази сферичної хвиліС) на кут 2α = π/2(рис. Д3.1). Природньо, зони Френеля ми розташовуємо у площиніА. Хоч хвиліC′,S′когерентні і повинні створювати інтерференційну картину, результуюча інтенсивність

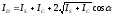(Д3.1)

дорівнює простій сумі інтенсивностей інтерферуючиххвиль, оскількиα = π/2. Очевидне співвідношення між інтенсивностями двох хвиль:.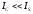

Поставимо на оптичній осі лінзу L так, щоб у спряженій з A площині E отримати зображення B′ то-чки B (рис. Д3.2). Освітленість екрана E у довільній точці x утворюється двома когерентними хвилями – C′, що дифрагувала на об’єкті B, та залишками прямої хвилі S′, яка пройшла по всій площі A (крім малої області B) і не брала участі у дифракції на об’єкті B. Розподіл інтенсивностей цих хвиль умовно зображено на рис. Д3.2. Очевидно, знову отримуємо рівномірно освітлене поле на екрані E, тобто, у будь-якій точці x результуюча інтенсивність складається з суми двох

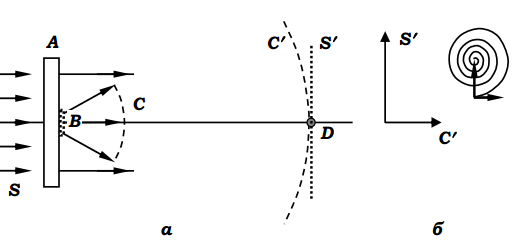
Рис. Д3.1. Падаюча плоска хвиля S та розсіяна на

об’єкті B сферична хвиля C; D – точка на осі, в яку

приходять обидві хвилі (а). Співвідношення між фаза-

ми кожної із хвиль у віддаленій точці D (б).

Рис. Д3.2. Утворення зображення в ФКМ.

ль у цій точці x . Звернувшись до формули (Д3.1), мусимо констатувати: у будь-якій точці екрану E різниця фаз інтерферуючих хвиль строго дорівнює π/2 (хоча сама фаза плоскої хвилі змінюється квадратично при віддалені точки x від центра до периферії).

Другий суттєвий момент явища – інтерференція когерентних хвиль відбувається в спільній області перекриття цих хвиль. Цей очевидний факт зводить нанівець існуючі популярні пояснення роботи ФКМ. З тих пояснень виходить, що в ФКМ видима картина являє собою амплітудну модуляцію, яка однозначно пропорційна фазовій, однак це не так Очевидно, щоб суттєво змінити розподіл інтенсив ності на екрані E в області точки B′, зробити її зримою, треба в рівнянні (Д3.1) довести різницю фаз до 0° або 180° - це і досягається встановленням у фокальній площині F, де збирається вся хвиля S, тонкої фазової пластинки, яка створює відповідне запізнення хвилі S′ на π/2 або на 3π/2. Додатковий виграш в контрасті буде, якщо приблизно вирівняти інтенсивності інтерферуючих полів. Практично для цього потрібно ослабити хвилю S′, тобто, фільтр в площині F мусить бути амплітудно-фазовим. 302 Розглянемо приклад. На пластинці A (рис. Д3.2) міститься тонкий шар рідини – пляма діаметром λ і товщиною λ/10. В полі E мікроскопа при цьому буде видно світле кільце на сірому фоні. Збільшимо діаметр плями до 10λ (100 λ, 1000 λ) при незмінній товщині λ/10. В полі зору ФКМ будемо бачити на сі рому тлі світле кільце діаметром 10 λ (100 λ, 1000 λ), причому в середині кільця таке ж сіре тло, як і ззовні його. Це означає, що у ФКМ спостерігається не сама функція ϕ, а її похідна ϕ/dxd . Вказаний ефект з очевидністю спостерігається на всіх фотографіях, починаючи з перших наукових повідомлень Ф. Церніке (рис. Д3.3). Зображення в ФКМ виглядає більш складно, оскільки має місце невідповідність обраної моделі (точкова неоднорідність) і реального просторового об’єкту. Проте висновки, отримані в даній моделі, є правильними – сигнал на виході пропорційний похідній від сигналу на вході.

Рис. Д.3. Фотографія зображення в ФКМ [14].