
- •Визначений інтеграл та його застосування.
- •1. Задачі, що приводять до поняття визначеного інтеграла.
- •2. Означення та умови існування визначеного інтеграла.
- •Приклади обчислення визначеного інтеграла. За означенням.
- •4. Властивості визначеного інтеграла.
- •5. Інтеграл зі змінною верхньою межею. Формула Ньютона–Лейбніца.
- •6. Приклади використання формули Ньютона–Лейбніца.
- •7. Заміна змінної та інтегрування за частинами у визначеному інтегралі.
- •Невласні інтеграли I роду.
- •9. Невласні інтеграли II роду.
- •Приклади дослідження невласних інтегралів на абсолютну та умовну збіжність.
- •14. Обчислення площ плоских фігур.
- •15. Обчислення довжин дуг кривих ліній.
- •16. Обчислення об’ємів тіл.
- •17. Обчислення площ поверхонь тіл обертання.
- •18. Фізичні застосування визначеного інтеграла.
- •19. Наближене обчислення визначених інтегралів.
- •Рекомендована література. Базова.
- •Допоміжна
15. Обчислення довжин дуг кривих ліній.
Нехай
задано дугу
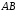 графіка функції
графіка функції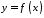 ,
яку будемо вважати
,
яку будемо вважати
неперервною
та неперервно диференційовною на
відрізку
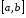 (рис. 15)
(рис. 15)
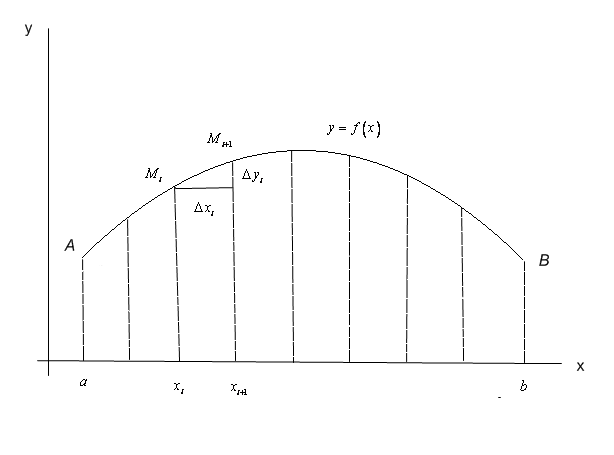
Рис. 15.
Розіб’ємо
відрізок
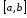 довільно обраними точками ділення на
частинні :
довільно обраними точками ділення на
частинні :
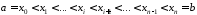 .
.
Відмітимо
на графіку функції точки
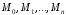 з абсцисами відповідно
з абсцисами відповідно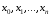 .
З’єднаємо їх відрізками прямих ліній.
Дістанемо ламану лінію
.
З’єднаємо їх відрізками прямих ліній.
Дістанемо ламану лінію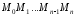 ,
яку вписано в дугу
,
яку вписано в дугу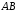 .
Позначимо периметр цієї ламаної через
.
Позначимо периметр цієї ламаної через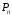 .
.
Означення.
Якщо існує і не залежить від способу
вписування ламаної скінченна границя
периметра цієї ламаної, коли найбільший
її відрізок прямує до нуля, то крива
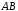 називаєтьсяспрямною,
а величина цієї границі називається
довжиною дуги і позначається
називаєтьсяспрямною,
а величина цієї границі називається
довжиною дуги і позначається
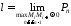 .
(15.1)
.
(15.1)
Позначимо
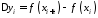 ,
,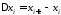 ,
,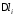 – довжину відрізка
– довжину відрізка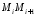 .
Очевидно, що
.
Очевидно, що
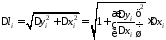 .
.
За
теоремою Лагранжа на інтервалі
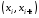 існує точка
існує точка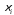 така, що
така, що
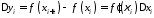 .
.
Тоді
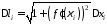 ,
,
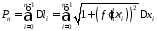 .
.
Це
є інтегральна сума для функції
 .
Оскільки
.
Оскільки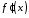 неперервна, функція
неперервна, функція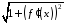 також неперервна, і тоді існує границя
(15.1):
також неперервна, і тоді існує границя
(15.1):
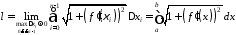 .
.
Отже дістали формулу:
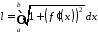 .
(15.2)
.
(15.2)
Приклад
1.
Обчислити довжину дуги напівкубічної
параболи
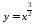 на відрізку
на відрізку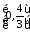 (рис. 16).
(рис. 16).
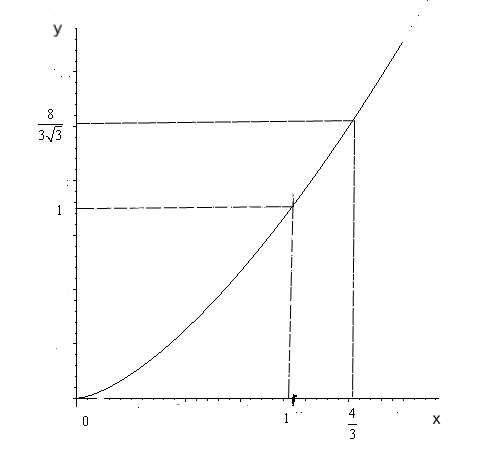
Рис. 16.
Маємо:
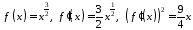 .
Отже
.
Отже
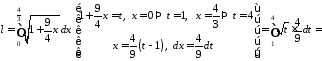
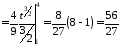 .
.
Приклад
2.
Обчислити довжину графіка функції
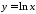 на відрізку
на відрізку .
.
Маємо:
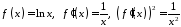 .
Отже
.
Отже
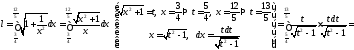
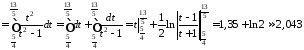 .
.
Якщо
криву
 задано параметрично:
задано параметрично: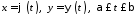 , де
, де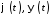 – неперервно диференційовні на проміжку
– неперервно диференційовні на проміжку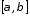 функції, то:
функції, то:
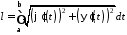 .
(15.3)
.
(15.3)
Приклад. Обчислити довжину однієї арки циклоїди, яка має параметричні рівняння:
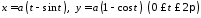 .
.
Циклоїда
– це лінія, яку описує точка на колі
радіуса
 ,
яке котиться вздовж прямої лінії. У
якості параметра
,
яке котиться вздовж прямої лінії. У
якості параметра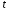 виступає кут поворота кола (рис. 17).
виступає кут поворота кола (рис. 17).
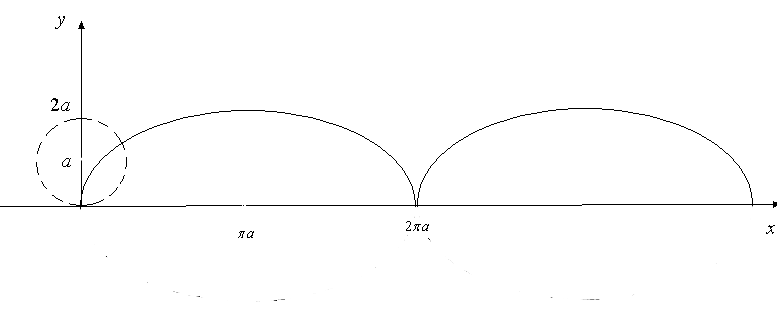
Рис. 17.
За формулою (15.3) маємо:
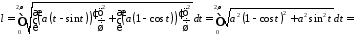

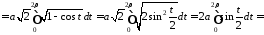
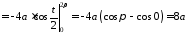 .
.
Якщо
криву задано у полярній системі координат
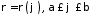 ,
де
,
де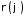 – неперервно диференційовна на
– неперервно диференційовна на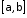 функція, то можна довести, що
функція, то можна довести, що
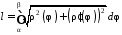 .
(15.4)
.
(15.4)
Приклад.
Обчислити довжину дуги логарифмічної
спіралі
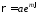
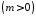 за умовою
за умовою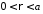 (рис. 18).
(рис. 18).
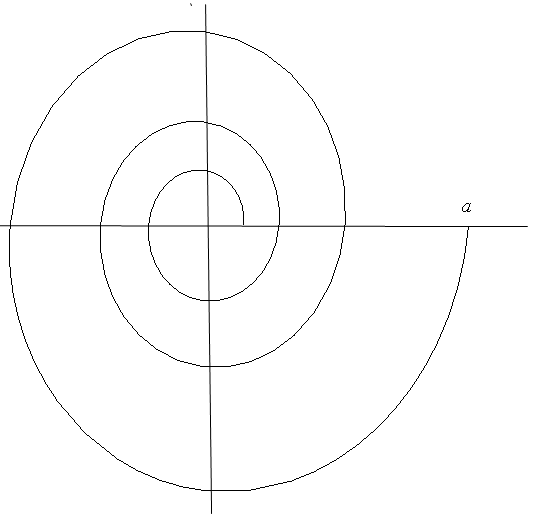
Рис. 18.
Внаслідок
того, що
 ,
дістаємо:
,
дістаємо: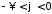 ,
отже за формулою (15.4) матимемо:
,
отже за формулою (15.4) матимемо:
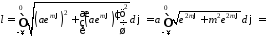
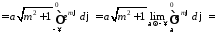
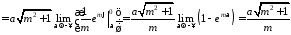
через
те, що
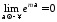 .
Зауважимо, що інтеграл, який тут виникає
– невласний 1-го роду.
.
Зауважимо, що інтеграл, який тут виникає
– невласний 1-го роду.
16. Обчислення об’ємів тіл.
Розглянемо
деяке тіло
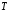 (рис.
19). Позначимо через
(рис.
19). Позначимо через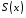 площу перерізу цього тіла площиною, яка
проходить перпендикулярно деякій осі
через точку з координатою
площу перерізу цього тіла площиною, яка
проходить перпендикулярно деякій осі
через точку з координатою на цій осі
на цій осі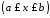 .
.
Розіб’ємо
відрізок
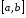 на частинні відрізки точками:
на частинні відрізки точками:
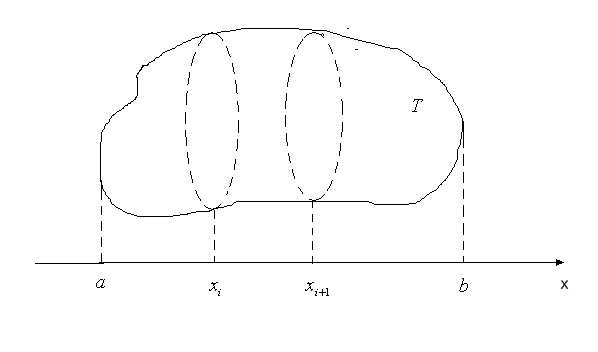
Рис. 19.
і
проведемо через ці точки площини,
перпендикулярні відрізку
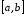 .
На кожному з частинних відрізків
.
На кожному з частинних відрізків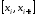 оберемо довільну точку
оберемо довільну точку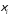 .
Площини розбивають наше тіло
.
Площини розбивають наше тіло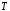 на елементарні циліндри
на елементарні циліндри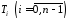 .
Площа основи циліндра
.
Площа основи циліндра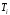 дорівнює
дорівнює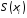 ,
а висота
,
а висота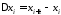 .
Сумарний об’єм
всіх циліндрів:
.
Сумарний об’єм
всіх циліндрів:
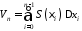 .
.
Границя
цієї суми при
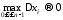 (якщо вона існує) називається об’ємом
даного тіла. Очевидно, що
(якщо вона існує) називається об’ємом
даного тіла. Очевидно, що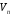 – це інтегральна сума для функції
– це інтегральна сума для функції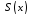 ,
отже об’єм
тіла
,
отже об’єм
тіла
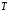 :
:
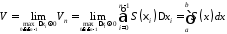 .
.
Таким чином доведено формулу:
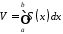 .
(16.1)
.
(16.1)
Розглянемо,
зокрема, об’єм
 тіла, яке утворено обертанням фігури,
обмеженої графіком функції
тіла, яке утворено обертанням фігури,
обмеженої графіком функції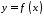 ,
відрізком
,
відрізком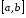 осі
осі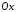 та прямими
та прямими
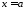 та
та
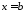 , навколо осі
, навколо осі (рис. 20).
(рис. 20).
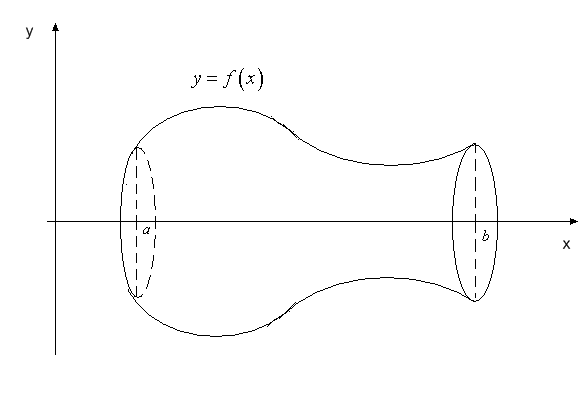
Рис. 20.
Тоді
площа перерізу
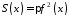 ,
і згідно з формулою (16.1):
,
і згідно з формулою (16.1):
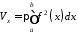 .
(16.2)
.
(16.2)
Якщо
така ж сама фігура обертається навколо
осі
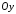 ,
то можна довести, що об’єм
,
то можна довести, що об’єм
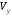 утвореного тіла дорівнює:
утвореного тіла дорівнює:
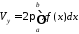 .
(16.3)
.
(16.3)
Нехай
тепер рівняння лінії, що обмежує нашу
фігуру, задано у параметричній формі:
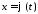 ,
,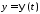 ,
,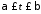 ,
причому функція
,
причому функція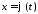 припускається неперервно диференційовною,
а функція
припускається неперервно диференційовною,
а функція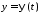 – неперервною на відрізку
– неперервною на відрізку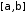 .
Тоді, якщо фігура обертається навколо
осі
.
Тоді, якщо фігура обертається навколо
осі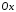 ,
то об’єм утвореного тіла дорівнює:
,
то об’єм утвореного тіла дорівнює:
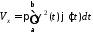 .
(16.4)
.
(16.4)
Якщо
та ж сама фігура обертається навколо
осі
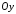 ,
то об’єм утвореного тіла дорівнює:
,
то об’єм утвореного тіла дорівнює:
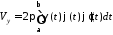 .
(16.5)
.
(16.5)
Нарешті
розглянемо у полярній системі координат
фігуру, яку обмежено променями
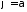 ,
,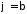 (
( )
та графіком функції
)
та графіком функції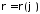 .
Тоді об’єм тіла, утвореного обертанням
цієї фігури навколо полярної осі,
дорівнює:
.
Тоді об’єм тіла, утвореного обертанням
цієї фігури навколо полярної осі,
дорівнює:
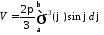 .
(16.6)
.
(16.6)
Приклади.
1. Знайти об’єм еліпсоїда
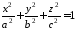 .
.
У
перерізі еліпсоїда площиною, паралельною
площині
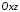 на відстані
на відстані
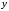 від
неї утворюється еліпс:
від
неї утворюється еліпс:
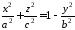 ,
,
або:
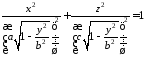 .
.
Півосі
цього еліпса
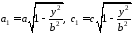 ,
і його площа дорівнює (див. приклад після
формули (14.2)):
,
і його площа дорівнює (див. приклад після
формули (14.2)):
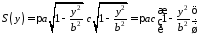 .
.
Тому за формулою (16.1) маємо:
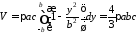
(перевірте
самостійно). Зокрема, якщо
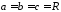 ,
дістаємо формулу об’єму кулі:
,
дістаємо формулу об’єму кулі:
 .
.
2.
Знайти об’єм тіла, утвореного обертанням
графіка функції
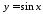 навколо відрізка
навколо відрізка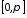 осі
осі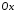 .
.
За формулою (16.2) маємо:
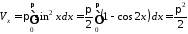 .
.
3.
Знайти об’єм тіла, утвореного обертанням
фігури, обмеженої графіком функції
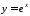 ,
відрізком
,
відрізком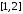 осі
осі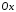 ,
та прямими
,
та прямими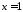 ,
,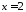 :
а) навколо осі
:
а) навколо осі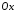 ;
б) навколо осі
;
б) навколо осі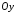 .
.
Об’єм
тіла, утвореного обертанням даної фігури
навколо осі
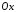 ,
знайдемо за формулою (16.2):
,
знайдемо за формулою (16.2):
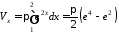 .
.
Об’єм
тіла, утвореного обертанням тієї ж
фігури навколо осі
 ,
знайдемо за формулою (16.3):
,
знайдемо за формулою (16.3):
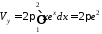 .
.
4.
Знайти об’єм тіла, утвореного обертанням
фігури, обмеженої аркою циклоїди
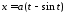 ,
,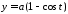 ,
,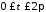 навколо: а) осі
навколо: а) осі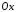 ;
б) осі
;
б) осі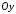 .
.
Об’єм
тіла, утвореного обертанням навколо
осі
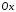 ,
знайдемо за формулою (16.4):
,
знайдемо за формулою (16.4):
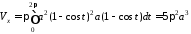 .
.
Об’єм
тіла, утвореного обертанням навколо
осі
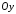 ,
знайдемо за формулою (16.5):
,
знайдемо за формулою (16.5):
 (обчислення
інтегралів перевірте самостійно).
(обчислення
інтегралів перевірте самостійно).
5.
Знайти об’єм тіла, утвореного обертанням
фігури, обмеженої кардіоїдою
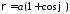 ,
,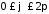 ,
навколо полярної осі.
,
навколо полярної осі.
Внаслідок
симетрії кардіоїди відносно полярної
осі (рис. 14), тіло, яке утворено обертанням
всієї кардіоїди навколо полярної осі,
співпаде з тілом, яке утворено обертанням
тільки верхньої половини кардіоїди,
яка відповідає зміні кута
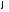 від
від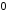 до
до .
Тоді, користуючись формулою (16.6),
дістанемо:
.
Тоді, користуючись формулою (16.6),
дістанемо:
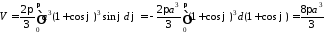 .
.
