
- •Визначений інтеграл та його застосування.
- •1. Задачі, що приводять до поняття визначеного інтеграла.
- •2. Означення та умови існування визначеного інтеграла.
- •Приклади обчислення визначеного інтеграла. За означенням.
- •4. Властивості визначеного інтеграла.
- •5. Інтеграл зі змінною верхньою межею. Формула Ньютона–Лейбніца.
- •6. Приклади використання формули Ньютона–Лейбніца.
- •7. Заміна змінної та інтегрування за частинами у визначеному інтегралі.
- •Невласні інтеграли I роду.
- •9. Невласні інтеграли II роду.
- •Приклади дослідження невласних інтегралів на абсолютну та умовну збіжність.
- •14. Обчислення площ плоских фігур.
- •15. Обчислення довжин дуг кривих ліній.
- •16. Обчислення об’ємів тіл.
- •17. Обчислення площ поверхонь тіл обертання.
- •18. Фізичні застосування визначеного інтеграла.
- •19. Наближене обчислення визначених інтегралів.
- •Рекомендована література. Базова.
- •Допоміжна
Приклади дослідження невласних інтегралів на абсолютну та умовну збіжність.
Приклад 1. Дослідити на абсолютну та умовну збіжність інтеграл
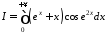 .
.
Зробимо
заміну змінної
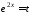 ,
тоді
,
тоді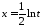 ,
,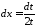 ,
тому
,
тому
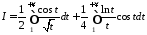 .
(13.1)
.
(13.1)
Функція
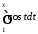 обмежена, а функції
обмежена, а функції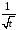 та
та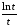 монотонно прямують до нуля при
монотонно прямують до нуля при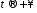 ,
отже обидва інтеграли в (13.1) збіжні за
ознакою Діріхле, отже інтеграл
,
отже обидва інтеграли в (13.1) збіжні за
ознакою Діріхле, отже інтеграл збіжний. Покажемо, що інтеграл
збіжний. Покажемо, що інтеграл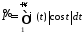 ,
де
,
де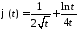 ,
розбіжний. Дійсно,
,
розбіжний. Дійсно,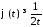 при
при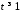 ;
;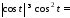
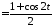 .
.
Розглянемо
інтеграл
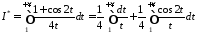 .
Перший з цих інтегралів розбіжний, а
другий збіжний за ознакою Діріхле, отже
інтеграл
.
Перший з цих інтегралів розбіжний, а
другий збіжний за ознакою Діріхле, отже
інтеграл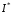 розбіжний. Тоді за теоремою 2 інтеграл
розбіжний. Тоді за теоремою 2 інтеграл розбіжний, отже інтеграл
розбіжний, отже інтеграл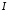 збігається умовно.
збігається умовно.
Приклад 2. Дослідити на абсолютну та умовну збіжність інтеграл Френеля:
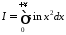 .
.
Маємо:
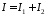 ,
де
,
де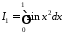 ,
,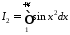 .
Інтеграл
.
Інтеграл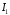 – звичайний власний інтеграл Рімана,
тому питання про збіжність інтеграла
– звичайний власний інтеграл Рімана,
тому питання про збіжність інтеграла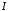 рівносильне питанню про збіжність
інтеграла
рівносильне питанню про збіжність
інтеграла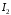 .
В інтегралі
.
В інтегралі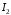 зробимо заміну:
зробимо заміну: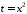 .
Тоді
.
Тоді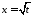 ,
,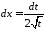 ,
отже
,
отже
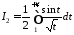 .
.
Звідси
видно, що цей інтеграл збіжний за ознакою
Діріхле (функція
 обмежена, а функція
обмежена, а функція
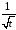 монотонно прямує до нуля при
монотонно прямує до нуля при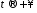 ).
Покажемо, що він збіжний умовно. Дійсно,
оскільки
).
Покажемо, що він збіжний умовно. Дійсно,
оскільки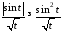 ,
а інтеграл
,
а інтеграл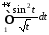 розбіжний (див. п. 11, приклад 1), то розбіжним
є інтеграл
розбіжний (див. п. 11, приклад 1), то розбіжним
є інтеграл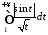 ,
отже інтеграл
,
отже інтеграл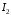 збіжний умовно, а тоді збіжний умовно
й інтеграл
збіжний умовно, а тоді збіжний умовно
й інтеграл .
.
Аналогічні
висновки стосуються й другого інтеграла
Френеля
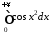 .
.
Приклад 3. Дослідити на абсолютну та умовну збіжність інтеграл
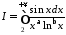 .
.
Пригадаємо (п. 10, приклад 5), що інтеграл
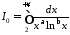 збігається
при
збігається
при
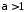 та при
та при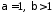 ,
і розбіжний при всіх інших
,
і розбіжний при всіх інших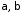 .
.
Розглянемо окремо випадки.
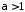 .
Оскільки
.
Оскільки
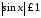 ,
а інтеграл
,
а інтеграл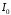 збігається, то інтеграл
збігається, то інтеграл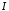 збігається абсолютно.
збігається абсолютно.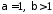 .
Також інтеграл
.
Також інтеграл
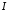 збігається абсолютно.
збігається абсолютно.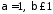 .
Оскільки
.
Оскільки
 ,
і функція
,
і функція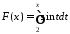 обме-
обме-
жена,
то інтеграл
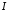 збігається за ознакою Діріхле. Розглянемо:
збігається за ознакою Діріхле. Розглянемо:
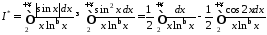 .
.
Перший
з цих інтегралів розбіжний (обчислюється
безпосередньо), а другий збіжний (за
ознакою Діріхле). Таким чином інтеграл
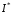 розбіжний, отже інтеграл
розбіжний, отже інтеграл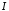 збігається умовно.
збігається умовно.
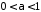 .
Оскільки
.
Оскільки
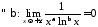 ,
і функція
,
і функція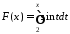 об-
об-
межена,
то інтеграл
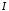 збіжний за ознакою Діріхле. Розглянемо:
збіжний за ознакою Діріхле. Розглянемо:
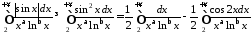 .
.
Перший
з цих інтегралів розбіжний, а другий
збіжний (за ознакою Діріхле), отже
інтеграл
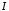 збіжний умовно.
збіжний умовно.
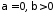 .
Інтеграл збіжний за ознакою Діріхле
(функція
.
Інтеграл збіжний за ознакою Діріхле
(функція
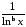 моно-
моно-
тонно
прямує до нуля при
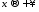 ,
функція
,
функція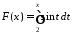 обмежена).
обмежена).
Розглянемо:
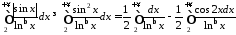 .
.
Перший
з цих інтегралів розбіжний, а другий
збіжний за ознакою Діріхле, отже інтеграл
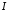 збіжний умовно.
збіжний умовно.
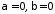 .
У цьому випадку отримуємо інтеграл
.
У цьому випадку отримуємо інтеграл
 ,
який, оче-
,
який, оче-
видно, розбіжний.
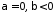 .
Позначивши
.
Позначивши
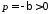 ,
запишемо
,
запишемо у вигляді:
у вигляді:
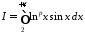 .
.
Доведемо
наступний результат. Нехай
функція
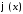 неперервна та додатна на
неперервна та додатна на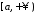 ,
,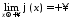 .
Тоді інтеграл
.
Тоді інтеграл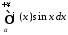 розбіжний.
розбіжний.
Скористаємось
критерієм Коші. Покажемо, що існує
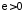 таке, що для будь якого
таке, що для будь якого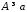 знайдуться
знайдуться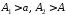 такі, що
такі, що
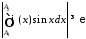 .
(13.2)
.
(13.2)
Візьмемо
для довільного
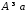 натуральне число
натуральне число так, щоб
так, щоб .
Тоді
.
Тоді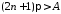 ,
і покладемо
,
і покладемо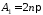 ,
,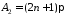 .
Оскільки на відрізку
.
Оскільки на відрізку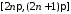 функція
функція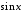 не змінює знаку та інтегровна, то на
підставі теореми про середнє значення
існує
не змінює знаку та інтегровна, то на
підставі теореми про середнє значення
існує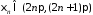 таке, що
таке, що
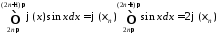 .
.
Тоді
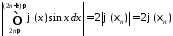 .
.
Оскільки
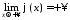 ,
,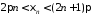 ,
то
,
то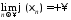 .
Отже завжди можна обрати
.
Отже завжди можна обрати настільки великим, щоб
настільки великим, щоб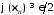 .
І тоді рівність (13.2) виконано, тобто
згідно критерію Коші інтеграл
.
І тоді рівність (13.2) виконано, тобто
згідно критерію Коші інтеграл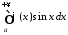 розбіжний. З цього результату одразу ж
випливає розбіжність інтеграла
розбіжний. З цього результату одразу ж
випливає розбіжність інтеграла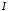 ,
оскільки функція
,
оскільки функція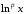 при
при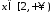 неперервна, додатна, і
неперервна, додатна, і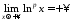 .
.
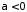 .
Позначивши
.
Позначивши
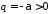 ,
запишемо інтеграл у вигляді:
,
запишемо інтеграл у вигляді:
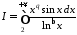 .
.
Функція
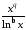 при
при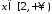 та
та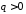 неперервна, додатна, і
неперервна, додатна, і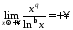 .
Тому на підставі того ж твердження,
інтеграл
.
Тому на підставі того ж твердження,
інтеграл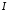 розбіжний.
розбіжний.
Отже
остаточно, інтеграл
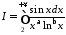
при
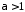 збігається абсолютно
збігається абсолютно ;
;
при
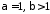 збігається абсолютно;
збігається абсолютно;
при
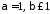 збігається умовно;
збігається умовно;
при
 збігається умовно
збігається умовно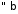 ;
;
при
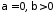 збігається умовно;
збігається умовно;
при
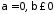 розбігається;
розбігається;
при
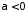 розбігається
розбігається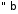 .
.
У відомій кінострічці «Зустріч на далекому меридіані» за романом Мітчела Уїлсона два головних персонажа фізики намагаються з’ясувати причини розбіжності у своїх дослідженнях між експериментальними даними і теоретичними результатами. І виявилося, що справа в тому, що вони не дослідили на збіжність один з інтегралів, що там виникало. А він оказався розбіжним, чого вони не врахували і працювали з ним як із збіжним. Ось для чого і фізикам доводиться займатися викладеними вище питаннями.
