
- •Визначений інтеграл та його застосування.
- •1. Задачі, що приводять до поняття визначеного інтеграла.
- •2. Означення та умови існування визначеного інтеграла.
- •Приклади обчислення визначеного інтеграла. За означенням.
- •4. Властивості визначеного інтеграла.
- •5. Інтеграл зі змінною верхньою межею. Формула Ньютона–Лейбніца.
- •6. Приклади використання формули Ньютона–Лейбніца.
- •7. Заміна змінної та інтегрування за частинами у визначеному інтегралі.
- •Невласні інтеграли I роду.
- •9. Невласні інтеграли II роду.
- •Приклади дослідження невласних інтегралів на абсолютну та умовну збіжність.
- •14. Обчислення площ плоских фігур.
- •15. Обчислення довжин дуг кривих ліній.
- •16. Обчислення об’ємів тіл.
- •17. Обчислення площ поверхонь тіл обертання.
- •18. Фізичні застосування визначеного інтеграла.
- •19. Наближене обчислення визначених інтегралів.
- •Рекомендована література. Базова.
- •Допоміжна
Приклади обчислення визначеного інтеграла. За означенням.
Наведемо приклади обчислення визначеного інтеграла, як кажуть, за означенням, тобто як границі інтегральних сум.
Приклад 1. Обчислити:
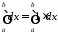 .
.
Розіб’ємо
відрізок
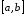 довільним
чином на частинні відрізки і складемо
інтегральну суму:
довільним
чином на частинні відрізки і складемо
інтегральну суму:
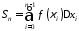 .
.
Незалежно
від обрання точок
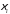 буде виконано:
буде виконано: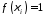 ,
тому:
,
тому:
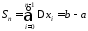 .
.
І отже:
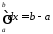 .
.
Приклад 2. Обчислити:
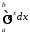 .
.
Оскільки
функція
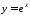 неперервна на всій числовій прямій,
вона інтегровна на відрізку
неперервна на всій числовій прямій,
вона інтегровна на відрізку .
Розіб’ємо
відрізок
.
Розіб’ємо
відрізок
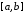 на
на рівних частинних відрізків точками
ділення
рівних частинних відрізків точками
ділення
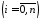 ,
де
,
де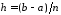 .
Очевидно, що
.
Очевидно, що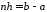 ,
,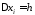
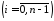 ,
,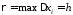 .
За точки
.
За точки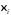 візьмемо
візьмемо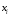
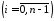 .
Складемо інтегральну суму:
.
Складемо інтегральну суму:
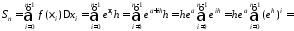
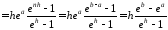 .
.
Тут ми скористалися формулою:
 .
.
Тоді
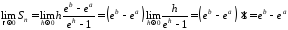 .
.
Отже
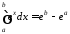 .
.
Приклад 3. Обчислити:
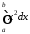 .
.
Оскільки
функція
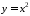 неперервна на всій числовій прямій,
вона інтегровна на відрізку
неперервна на всій числовій прямій,
вона інтегровна на відрізку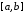 .
Розіб’ємо
відрізок
.
Розіб’ємо
відрізок
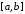 на
на рівних частинних відрізків точками
ділення
рівних частинних відрізків точками
ділення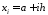
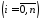 ,
де
,
де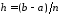 .
Очевидно, що
.
Очевидно, що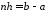 ,
,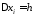
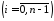 ,
,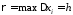 .
Таким чином у даному випадку умова
.
Таким чином у даному випадку умова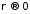 (або
(або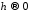 )
еквівалентна умові
)
еквівалентна умові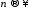 .
За точки
.
За точки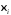 візьмемо
візьмемо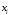
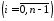 .
Складемо інтегральну суму:
.
Складемо інтегральну суму:
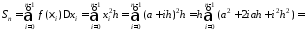
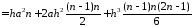 .
.
Тут скористалися формулами:
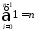 ,
,
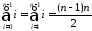 ,
,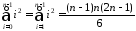 .
.
З
урахуванням рівності
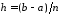 тепер маємо:
тепер маємо:
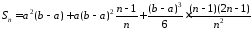 .
.
Звідси
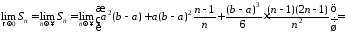
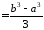 .
.
Отже
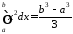 .
.
Вже
ці приклади показують, що обчислення
інтегралів за означенням досить складна
задача, навіть для відносно простих
функцій. Тому таким методом користуються
рідко. Нижче ми наведемо формулу, за
якою інтеграл обчислюється набагато
простіше. Щоправда, ця формула виводиться
у припущенні, що функція
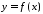 неперервна на відрізку
неперервна на відрізку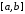 .
.
4. Властивості визначеного інтеграла.
Тут ми сформулюємо деякі важливі властивості визначеного інтеграла, які нам будуть потрібні у подальшому.
1. Величина визначеного інтеграла не залежить від позначення змінної інтегрування.
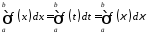 .
.
2. Якщо верхня межа інтегрування співпадає з нижньою, то інтеграл дорівнює нулю.
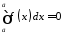 .
.
3. Від переставлення місцями меж інтегрування отримується інтеграл, який дорівнює даному з протилежним знаком.
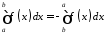 .
.
4.
Якщо функція
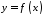 інтегровна
на максимальному з відрізків
інтегровна
на максимальному з відрізків
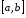 ,
,
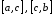 ,то
справедлива рівність:
,то
справедлива рівність:
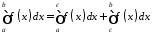 .
(4.1)
.
(4.1)
Доведення.
Припустимо
спочатку, що
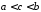 .
Розіб’ємо
відрізок
.
Розіб’ємо
відрізок
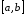 на
частинні так, щоб точка
на
частинні так, щоб точка
 була точкою розбиття, наприклад
була точкою розбиття, наприклад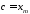 .
Тоді
.
Тоді
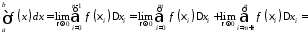
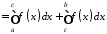 .
.
Цей факт добре ілюструється геометрично (рис. 4).
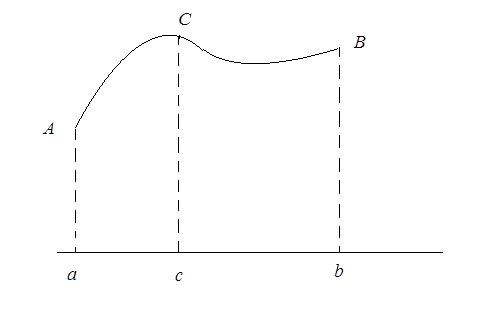
Рис. 4.

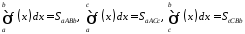 .
.
Формула
(4.1) зберігає справедливість і у випадку,
коли
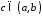 .
Припустимо, наприклад що
.
Припустимо, наприклад що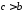 .
Тоді згідно за попереднім:
.
Тоді згідно за попереднім:
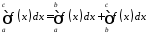 .
.
На підставі властивості 3 маємо:
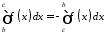 ,
і тоді:
,
і тоді:
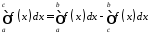 ,
а
звідси і випливає формула (4.1). Випадок
,
а
звідси і випливає формула (4.1). Випадок
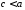 розглядається аналогічно.
розглядається аналогічно.
5. Сталий множник можна виносити за знак визначеного інтеграла:
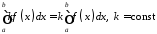 .
.
6.
Якщо функції
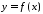 та
та інтегровні на відрізку
інтегровні на відрізку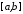 ,
то функції
,
то функції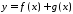 ,
,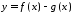 також інтегровні на відрізку
також інтегровні на відрізку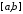 ,
причому:
,
причому:
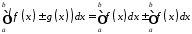 .
.
7.
Якщо функції
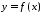 та
та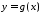 інтегровні на відрізку
інтегровні на відрізку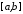 ,
то функція
,
то функція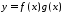 також інтегровна на відрізку
також інтегровна на відрізку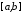 .
.
8.
Якщо
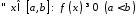 ,
то
,
то
 .
.
9.
Якщо
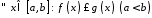 ,
то
,
то
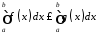 .
.
10.
Якщо функція
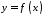 інтегровна на
інтегровна на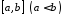 ,
то функція
,
то функція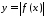 також інтегровна на відрізку
також інтегровна на відрізку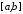 ,
причому:
,
причому:
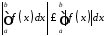 .
.
11.
Якщо
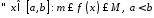 ,
то
,
то
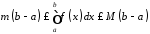 .
.
Дійсно
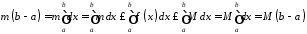 .
.
12.
Теорема
(про
середнє значення функції).
Нехай
функція
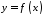 неперервна на відрізку
неперервна на відрізку
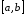 ,
а
функція
,
а
функція
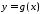 інтегровна на відрізку
інтегровна на відрізку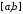 ,
і на відрізку
,
і на відрізку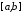 зберігає свій знак, тобто
зберігає свій знак, тобто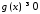 при
при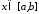 ,
або
,
або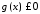 при
при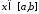 .
Тоді на відрізку
.
Тоді на відрізку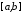 існує
точка
існує
точка така, що виконуватиметься рівність:
така, що виконуватиметься рівність:
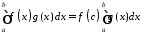 .
.
Доведення.
Нехай для визначеності
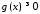 при
при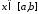 .
Оскільки функція
.
Оскільки функція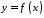 неперервна на відрізку
неперервна на відрізку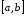 ,
то згідно з 2-ю теоремою Вейєрштрасса
ця функція досягає на цьому відрізку
свого найменшого та найбільшого значень
,
то згідно з 2-ю теоремою Вейєрштрасса
ця функція досягає на цьому відрізку
свого найменшого та найбільшого значень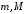 .
Тоді:
.
Тоді:
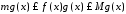 .
.
Внаслідок
неперервності функції
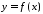 на відрізку
на відрізку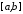 вона на цьому відрізку інтегровна, а,
оскільки функція
вона на цьому відрізку інтегровна, а,
оскільки функція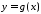 на відрізку
на відрізку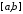 також інтегровна, то інтегровною на
також інтегровна, то інтегровною на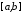 буде й функція
буде й функція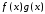 .
А тоді
.
А тоді
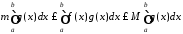 .
(4.2)
.
(4.2)
Якщо
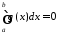 ,
то з (4.2) випливає, що
,
то з (4.2) випливає, що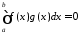 ,
і тоді твердження теореми доведено.
Нехай
,
і тоді твердження теореми доведено.
Нехай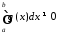 ,
тоді
,
тоді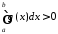 ,
оскільки
,
оскільки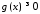 .
Тому:
.
Тому:
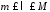 ,
,
де
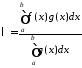 .
.
Внаслідок
неперервності функції
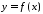 на відрізку
на відрізку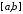 на підставі 2-ї теореми Больцано–Коші
на відрізку
на підставі 2-ї теореми Больцано–Коші
на відрізку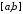 існує точка
існує точка така, що
така, що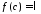 ,
тобто
,
тобто
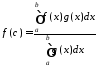 ,
,
звідки й випливає твердження теореми.
Наслідок.
Якщо, зокрема
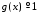 на
на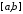 ,
то для неперервної на
,
то для неперервної на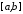 функції
функції існує
існує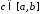 таке, що:
таке, що:
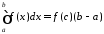 ,
,
оскільки
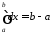 (див. п.3).
(див. п.3).
Величина
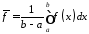 називаєтьсясереднім
значенням функції
називаєтьсясереднім
значенням функції
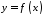 на відрізку
на відрізку .
.
Теорема про середнє значення та наслідок з неї дає можливість оцінювати величини інтегралів без їх безпосереднього обчислювання.
Приклад. Оцінити величину інтеграла:
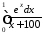 .
.
Покладемо
в теоремі про середнє значення
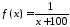 ,
,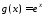 .
Тоді
.
Тоді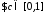 :
:
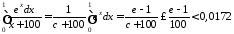
(тут
скористалися рівністю
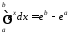 – див. п.3).
– див. п.3).
