
- •Визначений інтеграл та його застосування.
- •1. Задачі, що приводять до поняття визначеного інтеграла.
- •2. Означення та умови існування визначеного інтеграла.
- •Приклади обчислення визначеного інтеграла. За означенням.
- •4. Властивості визначеного інтеграла.
- •5. Інтеграл зі змінною верхньою межею. Формула Ньютона–Лейбніца.
- •6. Приклади використання формули Ньютона–Лейбніца.
- •7. Заміна змінної та інтегрування за частинами у визначеному інтегралі.
- •Невласні інтеграли I роду.
- •9. Невласні інтеграли II роду.
- •Приклади дослідження невласних інтегралів на абсолютну та умовну збіжність.
- •14. Обчислення площ плоских фігур.
- •15. Обчислення довжин дуг кривих ліній.
- •16. Обчислення об’ємів тіл.
- •17. Обчислення площ поверхонь тіл обертання.
- •18. Фізичні застосування визначеного інтеграла.
- •19. Наближене обчислення визначених інтегралів.
- •Рекомендована література. Базова.
- •Допоміжна
Невласні інтеграли I роду.
Поняття визначеного інтеграла Рімана, як ми бачили, має зміст для скінченного проміжку і для обмеженої на цьому проміжку функції. Якщо хоч би одна з цих умов не виконана, то інтеграла у власному розумінні не існує. Тому виникає необхідність поширити поняття інтеграла на випадки нескінченного проміжку та необмеженої функції. Відповідно виникають інші поняття – так званих невласних інтегралів I роду (у випадку нескінченного проміжку) та II роду (у випадку необмеженої на проміжку функції). Ми почнемо з поняття невласного інтеграла I роду.
Нехай
функція
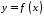 визначена на проміжку
визначена на проміжку
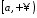 і інтегровна на будь якому відрізку
і інтегровна на будь якому відрізку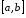 ,
де
,
де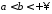 .
.
Означення.
Невласним
інтегралом I
роду
від функції
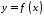 на проміжку
на проміжку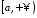 називається границя
називається границя
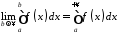 .
(8.1)
.
(8.1)
Якщо ця границя існує та скінченна, інтеграл (8.1) називається збіжним, у протилежному випадку – розбіжним.
Таким чином невласний інтеграл I роду не є границею інтегральних сум, а є границею визначеного інтеграла зі змінною верхньою межею. З геометричної точки зору він виражає площу необмеженої області (рис. 5).

Рис. 5.
Аналогічно
означається невласний інтеграл I
роду на проміжку
 :
:
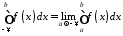 (8.2)
(8.2)
А також можливі невласні інтеграли з обома нескінченними межами:
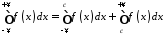 ,
(8.3) де
,
(8.3) де
 – довільне число. Інтеграл у лівій
частині формули (8.3) збігається тоді і
тільки тоді, коли незалежно один від
одного збігаються обидва інтеграли у
правій частині цієї формули.
– довільне число. Інтеграл у лівій
частині формули (8.3) збігається тоді і
тільки тоді, коли незалежно один від
одного збігаються обидва інтеграли у
правій частині цієї формули.
Приклади.
Дослідити на збіжність та у випадку збіжності обчислити інтеграл?
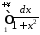 .
.
Маємо:
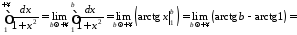
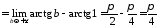 .
.
Отже
інтеграл збіжний, і його значення
дорівнює
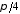 .
.
Дослідити на збіжність інтеграл
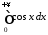 .
.
Маємо:
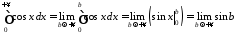 .
.
Відомо,
що функція
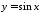 не має границі при
не має границі при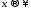 .
Отже даний інтеграл розбіжний.
.
Отже даний інтеграл розбіжний.
Дослідити на збіжність інтеграл
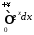 .
.
Маємо:
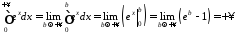 .
.
Отже даний інтеграл розбіжний (границя існує, але вона нескінченна).
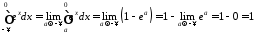 .
.
Даний інтеграл збіжний, і його значення дорівнює 1.
Визначимо, для яких значень параметра
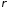 збігається інтеграл:
збігається інтеграл:
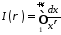 .
.
У
випадку
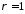 маємо:
маємо:
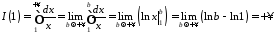 ,
тобто інтеграл розбіжний.
,
тобто інтеграл розбіжний.
Якщо
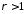 ,
то
,
то
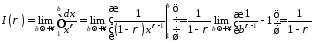 ,
отже інтеграл збіжний.
,
отже інтеграл збіжний.
Якщо
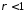 ,
то
,
то
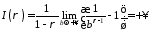 ,
і інтеграл розбіжний. Таким чином
,
і інтеграл розбіжний. Таким чином
 є збіжним, коли
є збіжним, коли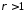 ,
і розбіжним, коли
,
і розбіжним, коли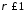 .
.
9. Невласні інтеграли II роду.
Розглянемо
тепер функцію
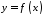 ,
яка визначена на півінтервалі
,
яка визначена на півінтервалі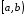 ,
і нехай виконана умова:
,
і нехай виконана умова:
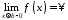 (9.1)
(9.1)
Точку
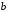 будемо називати особливою точкою функції
будемо називати особливою точкою функції .
У цій точці графік функції має вертикальну
асимптоту (рис. 6).
.
У цій точці графік функції має вертикальну
асимптоту (рис. 6).
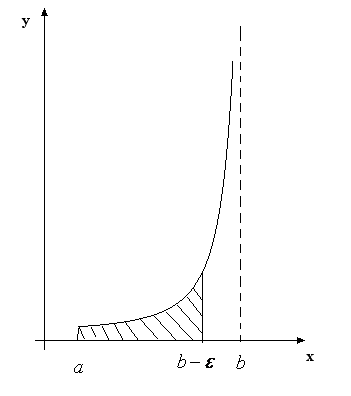
Рис. 6.
Нехай
функція
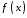 інтегровна на будь якому проміжку
інтегровна на будь якому проміжку
 ,
де
,
де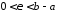 .
.
Означення.
Невласним
інтегралом II роду від функції
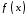 називається границя:
називається границя:
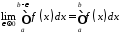 .
(9.2)
.
(9.2)
Якщо границя (9.2) існує і скінченна, то інтеграл називається збіжним, у протилежному випадку – розбіжним.
Якщо
особливою точкою функції
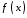 є точка
є точка ,
то:
,
то:
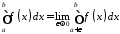 .
при умові, що функція
.
при умові, що функція
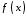 інтегровна на проміжку
інтегровна на проміжку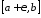 ,
де також
,
де також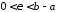 .
.
Нарешті,
якщо особливою точкою є деяка точка
 всередині проміжку
всередині проміжку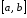 ,
то за означенням покладають:
,
то за означенням покладають:
 .
(9.3)
.
(9.3)
Якщо існують окремо скінченні границі
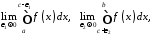 то
інтеграл у лівій частині рівності
(8.8.3) називається збіжним,
а якщо хоч би одна з цих границь не існує,
або нескінченна – розбіжним.
то
інтеграл у лівій частині рівності
(8.8.3) називається збіжним,
а якщо хоч би одна з цих границь не існує,
або нескінченна – розбіжним.
Якщо
особливими являються точки
 і
і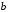 ,
то за означенням:
,
то за означенням:
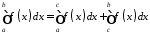 ,
де
,
де
 – довільна точка інтервалу
– довільна точка інтервалу .
Інтеграл у лівій частині рівності буде
збіжним тоді і тільки тоді, коли збіжні
обидва інтеграли у правій частині
рівності.
.
Інтеграл у лівій частині рівності буде
збіжним тоді і тільки тоді, коли збіжні
обидва інтеграли у правій частині
рівності.
З геометричної точки зору інтеграл II роду (9.2) також, як і невласний інтеграл I роду, виражає площу нескінченної фігури (рис. 7).
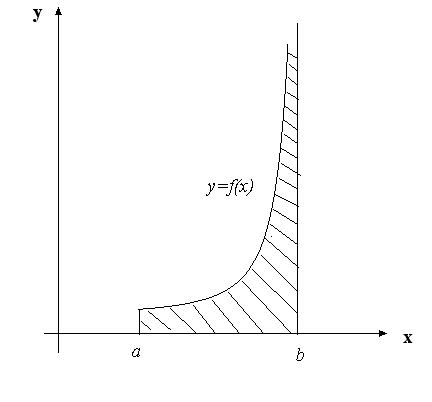
Рис. 7.
Але
якщо у випадку інтеграла I роду
нескінченність, так кажучи, відносно
осі
 (рис. 5), то тут – відносно осі
(рис. 5), то тут – відносно осі
 .
Фактично це така ж сама нескінченна
криволінійна трапеція, тільки повернута
на кут 90 градусів. А це свідчить про те,
що між невласними інтегралами I та II
роду існує певний зв’язок.
Дійсно, нехай, наприклад, особливою
точкою функції
.
Фактично це така ж сама нескінченна
криволінійна трапеція, тільки повернута
на кут 90 градусів. А це свідчить про те,
що між невласними інтегралами I та II
роду існує певний зв’язок.
Дійсно, нехай, наприклад, особливою
точкою функції
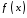 є точка
є точка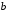 .
Тоді
.
Тоді
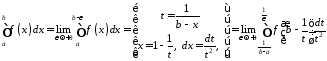 .
.
У останньому інтегралі позначимо:
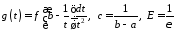 .
.
Якщо
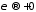 ,
то очевидно
,
то очевидно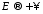 ,
і ми отримуємо:
,
і ми отримуємо:
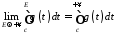 .
.
Таким чином звели невласний інтеграл II роду до невласного інтегралу I роду.
Приклади. Дослідити на збіжність і у випадку збіжності обчислити інтеграли.
1)
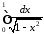 .
.
У
даному прикладі особливою є точка
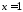 .
Маємо:
.
Маємо:
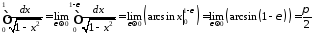 .
.
Отже
інтеграл збіжний, і його значення
дорівнює
 .
.
2)
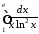 .
.
Особливою
є точка
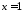 ,
оскільки
,
оскільки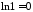 .
Маємо:
.
Маємо:
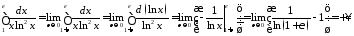
Отже інтеграл розбіжний.
3)
Встановити, для яких значень параметра
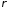 інтеграл збігається, а дл яких розбігається:
інтеграл збігається, а дл яких розбігається:
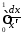 .
.
Якщо
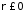 ,
то інтеграл не є невласним, оскільки
підінтегральна функція
,
то інтеграл не є невласним, оскільки
підінтегральна функція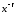 буде обмеженою на відрізку
буде обмеженою на відрізку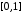 .
Отже залишилось дослідити випадок
.
Отже залишилось дослідити випадок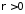 .
Тоді особливою точкою буде точка
.
Тоді особливою точкою буде точка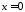 .
Нехай спочатку
.
Нехай спочатку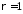 .
Маємо:
.
Маємо:
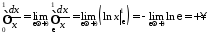 ,
отже
інтеграл розбіжний. Нехай тепер
,
отже
інтеграл розбіжний. Нехай тепер
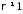 .
Тоді:
.
Тоді:
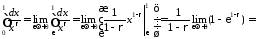
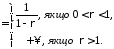
Отже
інтеграл збігається, якщо
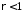 ,
і розбігається, якщо
,
і розбігається, якщо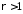 .
.
Повернемось до прикладу, який ми розглянули в п. 6, а саме до інтегралу
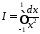 .
.
Ми
встановили, що безпосереднє використання
формули Ньютона
– Лейбніца
приводить до абсурдного результату –
інтеграл дорівнює від’ємному
числу, хоча зобов’язаний
бути додатним. Тепер ми можемо сказати,
що цей інтеграл невласний – особливою
є точка
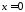 ,
яка належить інтервалу
,
яка належить інтервалу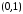 .
Розіб’ємо
цей інтеграл на два інтеграли
.
Розіб’ємо
цей інтеграл на два інтеграли
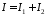 ,
де
,
де
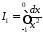 ,
,
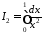 .
.
Оскільки,
як було встановлено в прикладі 3), інтеграл
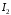 розбіжний, то розбіжним буде й інтеграл
розбіжний, то розбіжним буде й інтеграл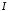 .
Таким чином про його обчислення взагалі
не може йти мова.
.
Таким чином про його обчислення взагалі
не може йти мова.
. Ознаки збіжності невласних інтегралів. I.
У багатьох випадках встановлювати збіжність інтеграла шляхом його безпосереднього обчислення досить складна задач. Тому якщо треба встановити тільки сам факт збіжності чи розбіжності, користуються деякими достатніми умовами збіжності.
Теорема
1.
Нехай
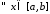 функція
функція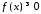 .
Тоді для збіжності невласного інтегралаI
роду
.
Тоді для збіжності невласного інтегралаI
роду
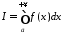 необхідно і достатньо, щоб функція
необхідно і достатньо, щоб функція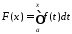 була обмежена зверху, тобто
була обмежена зверху, тобто
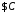 ,
,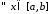 :
: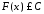 .
.
Доведення.
Достатність.
Нехай
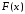 обмежена зверху. Оскільки
обмежена зверху. Оскільки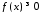 ,
то
,
то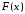 є неспадною, тобто монотонною. На підставі
теореми про границю монотонної та
обмеженої функції, існує
є неспадною, тобто монотонною. На підставі
теореми про границю монотонної та
обмеженої функції, існує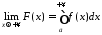 ,
тобто інтеграл
,
тобто інтеграл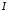 збіжний.
збіжний.
Необхідність.
Нехай інтеграл
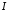 збіжний, тобто існує
збіжний, тобто існує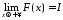 .
Тоді на підставі тієї ж теореми про
існування границі монотонної та обмеженої
функції маємо:
.
Тоді на підставі тієї ж теореми про
існування границі монотонної та обмеженої
функції маємо: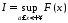 ,
і тоді
,
і тоді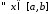 :
: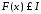 ,
тобто функція
,
тобто функція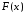 обмежена зверху.
обмежена зверху.
Теорема
2. Якщо
на проміжку
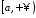 функції
функції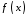 та
та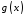 неперервні, та
неперервні, та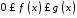 ,
то зі збіжності інтеграла
,
то зі збіжності інтеграла
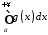 (10.1)
випливає
збіжність інтеграла
(10.1)
випливає
збіжність інтеграла
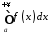 ,
(10.2) а
з розбіжності інтеграла
(10.2) випливає
розбіжність інтеграла
(10.1).
,
(10.2) а
з розбіжності інтеграла
(10.2) випливає
розбіжність інтеграла
(10.1).
Доведення.
I.
Оскільки функції
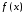 та
та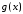 неперервні на
неперервні на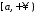 , вони інтегровні на будь якому проміжку
, вони інтегровні на будь якому проміжку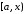 ,
де
,
де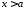 .
Оскільки
.
Оскільки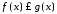 ,
то на підставі властивості 9 інтеграла
маємо, що
,
то на підставі властивості 9 інтеграла
маємо, що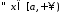 :
:
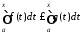 .
.
Оскільки
інтеграл (10.1) збігається, то за теоремою
1 функція
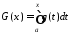 обмежена зверху, а тоді обмежена зверху
й функція
обмежена зверху, а тоді обмежена зверху
й функція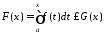 .
Тоді на підставі теореми 1 існує
.
Тоді на підставі теореми 1 існує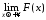 ,
тобто інтеграл (10.2) збіжний.
,
тобто інтеграл (10.2) збіжний.
II. Якщо інтеграл (10.2) розбіжний, то розбіжним буде і інтеграл (10.1), оскільки в протилежному випадку на підставі I інтеграл був би збіжним.
Теорема
3. Якщо
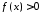 ,
,
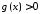
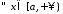 ,
таіснує
границя
,
таіснує
границя
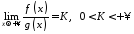 ,
то
інтеграли
(10.1), (10.2) водночас
обидва збігаються, або водночас
розбігаються.
,
то
інтеграли
(10.1), (10.2) водночас
обидва збігаються, або водночас
розбігаються.
Доведення. Нехай збігається інтеграл (10.1). З умови теореми маємо:
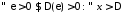 виконано
виконано
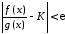 .
Або, що те ж саме:
.
Або, що те ж саме: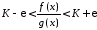 ,
звідки маємо
,
звідки маємо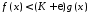 ,
якщо тільки
,
якщо тільки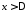 .
.
Оскільки
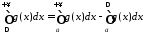 ,
то інтеграл
,
то інтеграл
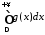 збіжний. Отже збіжний і інтеграл
збіжний. Отже збіжний і інтеграл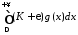 .
Тоді за теоремою 2 є збіжним інтеграл
.
Тоді за теоремою 2 є збіжним інтеграл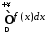 ,
а оскільки
,
а оскільки
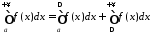 ,
то інтеграл (10.2) збіжний.
,
то інтеграл (10.2) збіжний.
Переписавши умову теореми у вигляді:
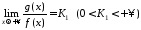 ,
де
,
де
 ,
отримаємо, що із збіжності інтеграла
(10.2) випливає збіжність інтеграла (10.1).
Таким чином інтеграли (10.1) та (10.2)
збігаються та розбігаються водночас,
а отже вони водночас і розбігаються.
,
отримаємо, що із збіжності інтеграла
(10.2) випливає збіжність інтеграла (10.1).
Таким чином інтеграли (10.1) та (10.2)
збігаються та розбігаються водночас,
а отже вони водночас і розбігаються.
Теореми, аналогічні теоремам 1 – 3, мають місце і для невласних інтегралів II роду.
Приклади.
Дослідити на збіжність інтеграл
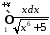 .
.
Маємо:
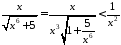 ,
а оскільки інтеграл
,
а оскільки інтеграл
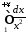 збігається
(це інтеграл
збігається
(це інтеграл
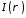 для
для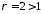 ),
то згідно з теоремою 1 збігається і наш
інтеграл.
),
то згідно з теоремою 1 збігається і наш
інтеграл.
Встановимо збіжність дуже важливого інтеграла Пуассона*:
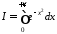 .
.
Зауважимо,
що
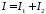 ,
де
,
де
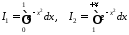 .
.
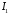 –це
інтеграл від обмеженої функції на
скінченному проміжку, і оскільки функція
–це
інтеграл від обмеженої функції на
скінченному проміжку, і оскільки функція
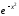 неперервна, інтеграл існує у власному
розумінні. Стосовно другого інтеграла
маємо:
неперервна, інтеграл існує у власному
розумінні. Стосовно другого інтеграла
маємо: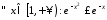 ,
а оскільки
,
а оскільки
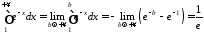 ,
тому
цей інтеграл збіжний, отже збіжний за
теоремою 1 інтеграл
,
тому
цей інтеграл збіжний, отже збіжний за
теоремою 1 інтеграл
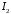 ,
а звідси випливає збіжність інтеграла
,
а звідси випливає збіжність інтеграла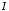 .
.
Дослідити на збіжність інтеграл
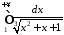 .
.
Маємо:
 ,
і
оскільки інтеграл
,
і
оскільки інтеграл
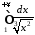 розбіжний
(це інтеграл
розбіжний
(це інтеграл
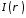 при
при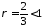 ),
то внаслідок теореми 2 розбіжний і наш
інтеграл.
),
то внаслідок теореми 2 розбіжний і наш
інтеграл.
Дослідити на збіжність інтеграл
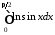 .
.
Особливою
точкою є точка
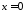 .
Оскільки
.
Оскільки
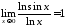 ,
то збіжність даного
інтегралу рівносильна збіжності
інтегралу
,
то збіжність даного
інтегралу рівносильна збіжності
інтегралу
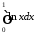 .
Тому розглянемо:
.
Тому розглянемо:
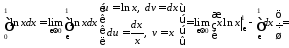
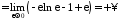 ,
тобто інтеграл розбіжний. А
отже розбіжний і початковий інтеграл.
,
тобто інтеграл розбіжний. А
отже розбіжний і початковий інтеграл.
З’ясувати, при яких значеннях параметрів
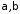 збігається, а при яких
збігається, а при яких
розбігається інтеграл:
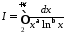 .
.
Розглянемо
три можливі випадки:
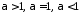 .
.
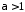 .
Тоді
.
Тоді
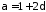 ,
де
,
де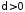 .
Запишемо підінтегральну функцію у ви-
.
Запишемо підінтегральну функцію у ви-
гляді:
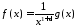 ,
де
,
де
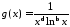 .
.
Оскільки
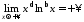 при
при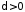 та
та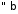 ,
то існує число
,
то існує число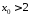 таке, що
таке, що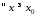 виконано:
виконано: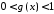 .
Тому при
.
Тому при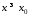 :
: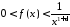 .
.
Інтеграл
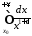 при
при збіжний, отже за теоремою 2 збіжний й
інтеграл
збіжний, отже за теоремою 2 збіжний й
інтеграл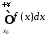 ,
а тоді збіжний й інтеграл
,
а тоді збіжний й інтеграл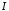 .
.
Таким
чином, якщо
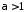 ,
то інтеграл
,
то інтеграл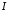 збіжний
збіжний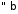 .
.
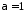 .
Тоді
.
Тоді
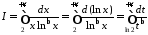 .
.
Цей
інтеграл збіжний при
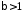 і розбіжний при
і розбіжний при (приклад 5, п. 8).
(приклад 5, п. 8).
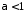 .
Тоді
.
Тоді
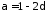 ,
,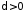 .
Подамо підінтегральну функцію у вигляді:
.
Подамо підінтегральну функцію у вигляді:
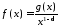 ,
де
,
де
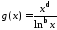 .
.
Маємо:
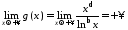 ,
отже існує число
,
отже існує число
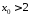 таке, що при
таке, що при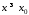 :
: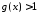 .
Тому при
.
Тому при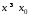 :
: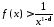 .
.
Інтеграл
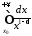 при
при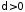 розбіжний, отже за теоремою 2 розбіжним
буде й інтеграл
розбіжний, отже за теоремою 2 розбіжним
буде й інтеграл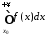 ,
а тоді розбіжним буде й інтеграл
,
а тоді розбіжним буде й інтеграл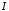 .
.
Таким
чином інтеграл
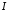 збігається при
збігається при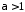 (
(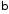 будь яке), при
будь яке), при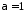 ,
,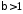 ,
і розбігається при всіх інших
,
і розбігається при всіх інших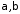 .
.
Дослідити на збіжність інтеграл:
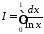 .
.
Цей
невласний інтеграл II
роду має дві особливі точки
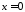 та
та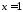 .
.
Подамо
інтеграл у вигляді
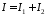 ,
де
,
де
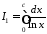 ,
,
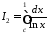 ,
,
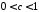 ,
і дослідимо окремо збіжність кожного
з цих інтегралів.
,
і дослідимо окремо збіжність кожного
з цих інтегралів.
а)
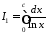 .
.
Зробимо
заміну змінної
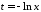 .
Тоді, якщо
.
Тоді, якщо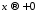 ,
то
,
то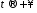 ,
і при
,
і при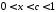 :
: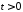 ;
;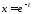 ,
,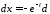 ,
і інтегралII
роду перетворюється на інтеграл I
роду:
,
і інтегралII
роду перетворюється на інтеграл I
роду:
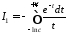 .
.
Розглянемо інтеграл
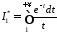 .
.
При
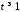 :
: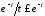 .
Інтеграл
.
Інтеграл збіжний, він дорівнює
збіжний, він дорівнює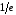 .
Тоді за теоремою 2 збіжний й інтеграл
.
Тоді за теоремою 2 збіжний й інтеграл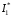 ,
отже збіжний й інтеграл
,
отже збіжний й інтеграл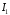 .
.
б)
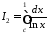 .
.
При
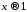 :
: ,
тобто
,
тобто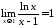 .
Розглянемо
.
Розглянемо
інтеграл
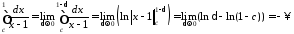 ,
,
отже
за теоремою 3 є розбіжним інтеграл
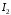 .
А тоді інтеграл
.
А тоді інтеграл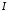 також розбіжний.
також розбіжний.
. Ознаки збіжності невласних інтегралів. II.
Теорема 4 (критерій Коші). Для збіжності невласного інтеграла
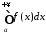 (11.1)
необхідно
і достатньо, щоб для будь якого
(11.1)
необхідно
і достатньо, щоб для будь якого
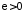 існувало таке число
існувало таке число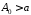 ,
щоб при
,
щоб при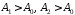 виконувалося нерівність:
виконувалося нерівність:
 .
(11.2)
.
(11.2)
Доведення.
Вводячи функцію
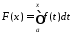 ,
умову теореми можна переписати так:
,
умову теореми можна переписати так:
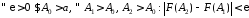 .
.
А
це є критерій Коші існування скінченної
границі
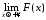 ,
тобто інтеграл (11.1) збігається тоді і
тільки тоді, коли виконано нерівність
(11.2).
,
тобто інтеграл (11.1) збігається тоді і
тільки тоді, коли виконано нерівність
(11.2).
Аналогічні твердження справедливі для невласних інтегралів II роду.
Теорема 5. Для збіжності невласного інтеграла
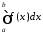 ,
(11.3)
,
(11.3)
де
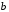 – особлива точка, необхідно і достатньо,
щоб для будь якого
– особлива точка, необхідно і достатньо,
щоб для будь якого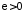 існувало
існувало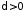 ,
що з нерівностей
,
що з нерівностей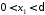 ,
,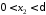 випливала нерівність
випливала нерівність
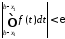 .
.
З теорем 4 та 5 випливає наступна ознака збіжності інтегралів (11.1), (11.3).
Теорема
6.
Якщо
збігається інтеграл
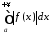 ,
то збігається інтег-
,
то збігається інтег-
рал (11.1).
Доведення.
З умови теореми на підставі теореми 4
маємо:
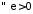
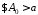 ,
що
,
що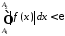 ,
якщо тільки
,
якщо тільки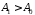 ,
,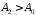 .
Але
.
Але
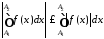 ,
,
отже
для тих самих
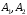 :
: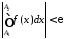 ,
звідки внаслідок теореми 4 випливає
збіжність інтеграла (11.1).
,
звідки внаслідок теореми 4 випливає
збіжність інтеграла (11.1).
Теорема
7.
Якщо
збігається інтеграл
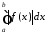 ,
де точка
,
де точка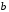 особлива, то збігається інтеграл (11.3).
особлива, то збігається інтеграл (11.3).
Зауваження.
Обернені твердження до теорем 6, 7
несправедливі, а саме із збіжності
інтегралів (11.1), (11.3) не випливає відповідно
збіжність інтегралів
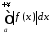 ,
,
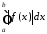 .
.
Означення.
Якщо інтеграл
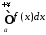 збігається, в той час, як інтеграл
збігається, в той час, як інтеграл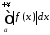 розбігається, то інтеграл
розбігається, то інтеграл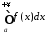 називаєтьсяумовно
збіжним.
Якщо разом з інтегралом
називаєтьсяумовно
збіжним.
Якщо разом з інтегралом
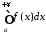 збігається і інтеграл
збігається і інтеграл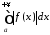 ,
то інтеграл
,
то інтеграл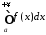 називаєтьсяабсолютно
збіжним.
називаєтьсяабсолютно
збіжним.
Аналогічні
означення вводяться і для інтегралів
II
роду. Іншими словами, невласний інтеграл
(I
чи II
роду) від функції
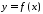 називається абсолютно збіжним, якщо
збіжний інтеграл від функції
називається абсолютно збіжним, якщо
збіжний інтеграл від функції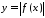 .
.
Приклади.
1. Дослідити на збіжність інтеграл
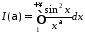 .
(11.4)
.
(11.4)
Нехай
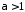 ;
тоді
;
тоді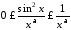 ,
і оскільки інтеграл
,
і оскільки інтеграл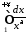 збігаєть-
збігаєть-
ся, то збіжним є й інтеграл (11.4).
Нехай
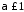 .
Покажемо, що інтеграл (11.4) розбігається.
Для цього
.
Покажемо, що інтеграл (11.4) розбігається.
Для цього
скористаємось
критерієм Коші, а саме покажемо, що існує
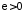 таке, що
таке, що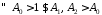 такі, що
такі, що
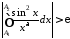 .
.
Нехай
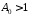 .
Покладемо
.
Покладемо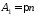 ,
,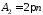 ,
де натуральне
,
де натуральне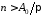 .
Тоді, оскільки при
.
Тоді, оскільки при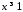 ,
,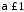 :
: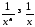 ,
то
,
то
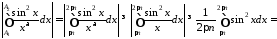
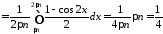 .
.
Таким
чином можемо взяти
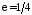 ,
і на підставі теореми 4 інтеграл розбіжний.
,
і на підставі теореми 4 інтеграл розбіжний.
2. Дослідити на абсолютну та умовну збіжність інтеграл
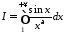 .
.
Нехай
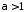 .
Тоді
.
Тоді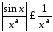 ,
і, оскільки інтеграл
,
і, оскільки інтеграл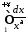 збіжний, то
збіжний, то
за
теоремою 2 збіжним є інтеграл
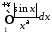 ,
отже інтеграл
,
отже інтеграл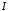 збіжний абсолютно.
збіжний абсолютно.
Нехай
 .
Інтегруючи за частинами, отримаємо:
.
Інтегруючи за частинами, отримаємо:
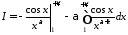 .
.
Оскільки
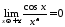 ,
а інтеграл
,
а інтеграл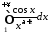 збіжний абсолютно, то
збіжний абсолютно, то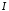 є збіжним.
є збіжним.
Розглянемо
інтеграл
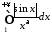 при
при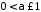 .
Маємо:
.
Маємо: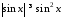 ,
а інтеграл
,
а інтеграл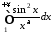 при
при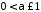 ,
як встановлено у попередньому прикладі,
розбігається, отже розбігається й
інтеграл
,
як встановлено у попередньому прикладі,
розбігається, отже розбігається й
інтеграл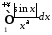 ,
а це означає, що інтеграл
,
а це означає, що інтеграл при
при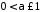 збігається умовно.
збігається умовно.
Нехай
 .
Доведемо на підставі критерію Коші, що
інтеграл
.
Доведемо на підставі критерію Коші, що
інтеграл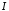
розбігається.
Задамо
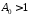 і оберемо
і оберемо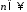 так, щоб
так, щоб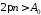 .
Покладемо:
.
Покладемо: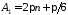 ,
,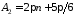 .
Для
.
Для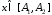 виконано
виконано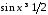 ,
і, крім того, при
,
і, крім того, при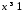 і
і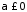 :
: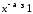 .
Отже маємо:
.
Отже маємо:
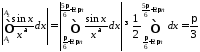 .
.
Таким
чином, обираючи в критерії Коші
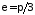 ,
отримуємо на його підставі, що інтеграл
,
отримуємо на його підставі, що інтеграл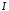 розбігається.
розбігається.
Отже
інтеграл
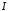 збігається абсолютно при
збігається абсолютно при ,
збігається умовно при
,
збігається умовно при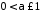 і розбігається при
і розбігається при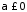 .
.
. Ознаки збіжності невласних інтегралів. III.
Теорема
8 (ознака
Діріхле). Нехай функція
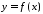 неперервна, а функція
неперервна, а функція
 має неперервну похідну на проміжку
має неперервну похідну на проміжку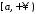 ,
і виконано наступні умови:
,
і виконано наступні умови:
функція
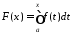 обмежена на
обмежена на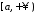 ,
тобто
,
тобто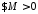
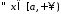 :
: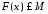 ;
;функція
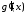 зберігає свій знак на
зберігає свій знак на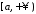 ,
тобто
,
тобто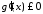 або
або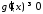 ;
;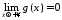 .
.
Тоді
інтеграл
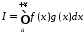 збігається.
збігається.
Доведення.
Скористаємось критерієм Коші, а саме
покажемо, що
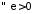
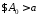
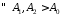 :
: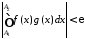 .
Інтегруючи за частинами, дістанемо:
.
Інтегруючи за частинами, дістанемо:
 .
.
З умови 1) теореми випливає, що:
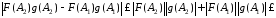
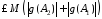 ,
,
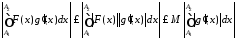 .
.
Якщо
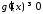 ,
то
,
то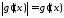 ,
а якщо
,
а якщо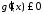 ,
то
,
то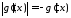 .
Тому, якщо
.
Тому, якщо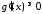 ,
то
,
то
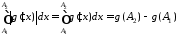 ,
,
а
якщо
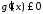 ,
то
,
то
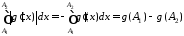 .
.
Отже
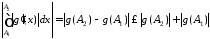 .
.
Тому
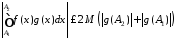 .
.
Згідно
з умовою 3) теореми:
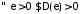
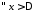 :
: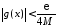 .
.
Тому,
якщо
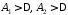 ,
то
,
то
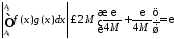 ,
і
таким чином, згідно критерію Коші,
інтеграл
,
і
таким чином, згідно критерію Коші,
інтеграл
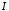 збігається.
збігається.
Теорему доведено.
Теорема
9
(ознака
Абеля). Якщо функція
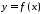 неперервна на проміжку
неперервна на проміжку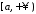 ,
інтеграл
,
інтеграл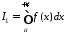 збігається, функція
збігається, функція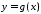 обмежена на
обмежена на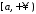 ,
та її похідна
,
та її похідна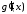 зберігає свій знак, то інтеграл
зберігає свій знак, то інтеграл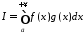 збігається.
збігається.
Доведення.
Оскільки
 зберігає свій знак, то функція
зберігає свій знак, то функція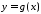 монотонна, і за теоремою про границю
монотонної та обмеженої функції існує
скінченна границя
монотонна, і за теоремою про границю
монотонної та обмеженої функції існує
скінченна границя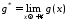 ,
тому функція
,
тому функція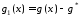 монотонно прямує до нуля при
монотонно прямує до нуля при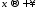 .
Оскільки інтеграл
.
Оскільки інтеграл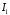 збіжний, то функція
збіжний, то функція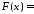
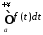 обмежена на
обмежена на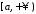 .
Тоді за ознакою Діріхле інтеграл
.
Тоді за ознакою Діріхле інтеграл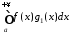 .
Але оскільки
.
Але оскільки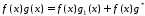 ,
то інтеграл
,
то інтеграл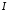 також збіжний.
також збіжний.
Аналогічні твердження справджуються для невласних інтегралів II роду.
Приклад. Дослідити на збіжність інтеграл
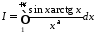 ,
,
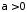 .
.
Оскільки
інтеграл
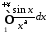 при
при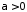 збіжний (п. 11, приклад 2), а функція
збіжний (п. 11, приклад 2), а функція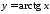 обмежена та монотонна, то за ознакою
Абеля інтеграл
обмежена та монотонна, то за ознакою
Абеля інтеграл збігається.
збігається.
