61. Сложение скоростей при сложном движении точки.

При сложном движении материальной точки её абсолютная скорость равна сумме относительной и переносной скоростей.

Движение точки можно рассматривать, как состоящее из двух движений: первое — движение относительно движущейся системы отсчёта, второе — движение вместе с движущейся системой относительно неподвижной. Такое движение точки называют сложным или составным.

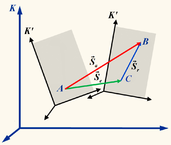
Пусть материальная точка в некоторый момент времени находилась в точке А, а через промежуток времени  оказалась в точке В (см. рис.). Тогда её перемещение относительно системы К (абсолютное перемещение) будет равно . Точка А подвижной системы K' за время переместилась вместе с K' и оказалась в точке С, совершив перемещение относительно системы К (переносное перемещение), изображённое на рисунке вектором . С точки зрения наблюдателя, связанного с системой K', точка С является той точкой, в которой МТ находилась первоначально, поэтому вектор  представляет собой перемещение МТ относительно подвижной системы K', то есть относительное перемещение. Из сказанного и векторной диаграммы на рисунке следует

Деля данное равенство на промежуток времени , а затем устремляя его к нулю, в пределе получаем

где  — абсолютная,  — переносная, а  — относительная скорость движения МТ.

Полученное равенство является математическим выражением теоремы о сложении скоростей, которая формулируется так:

При сложном движении абсолютная скорость материальной точки равна геометрической сумме переносной и относительной скоростей.

62,63,64

Когда_равна_нулю   Для определения направления кориолисова ускорения нужно спроецировать вектор относительной скорости в плоскость, перпендикулярную вектору переносной угловой скорости и полученную проекцию повернуть на   в сторону переносного вращения (рисунок 3.4).

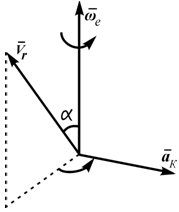
Рисунок 3.4

     Из формулы (3.5) видно, что кориолисово ускорение равно нулю, если

     - равна нулю относительная скорость;

     - переносное движение - поступательное (ω_e=0 );

     - угол между  ω_e  и V_r  равен 0^o  или 180_o  (вектор V_r  параллелен оси переносного вращения).

Определение_направления_и_модуля . Определение модуля и направления кориолисова ускорения

(24)

Известно, что модуль векторного произведения двух векторов равен

(25)

Еслито

(26)

Для определения направления вектора кориолисоваускорения надоспроектировать векторотносительной скорости точкина плоскость,перпендикулярную вектору(оси переносного вращения), и полученную проекциюповернуть в сторону этого вращения на.Полученное таким образомнаправление совпадает с направлением вектора(рис. 2, 3 и 4).Если точкадвижется в плоскости, перпендикулярной оси переносного вращения (вектору, тои формула (26) становится такой

(27)

Рис. 3. К определению направления вектор кориолисоваускорения при движении точки в пространстве

Кориолисово ускорение обращается в нуль, если:

1. - переносное движение поступательно или когда в данный момент

2. - относительная скорость в данный момент равна нулю.

3. Когда или, то есть когда векторпараллелен вектору.

А теперь рассмотрим фазы движения материальной точки вдоль горизонтально вращающегося стержня и покажем, что при совпадении вектровикориолисово ускорение выполняет функции ускорения, а когда эти векторы противоположны, то оно выполняет функции замедления(рис. 4). Вариации возможных сочетаний направления вектров переноснойи относительной скоростейматериальной точки, движущейся вдоль вращающегося стержня, представлены на рис. 4.

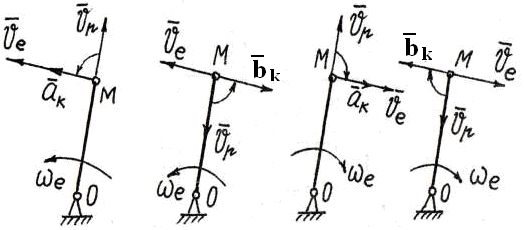
Рис. 4. Примеры определения направления векторовидля точки

    Абсолютное ускорение точки в сложном движении в общем случае определяется геометрической суммой пяти слагаемых

    Для определения величины абсолютного ускорения удобнее пользоваться аналитическим методом сложения векторов:

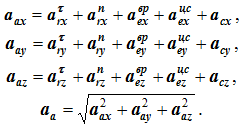
Ускорение кориолиса

Ускорение Кориолиса  можно получить, спроецировав вектор относительной скорости точки  на плоскость, перпендикулярную вектору переносной угловой скорости , увеличив полученную проекцию в  раз и повернув её на 90 градусов в направлении переносного вращения.

Способы вычисления ускорения Кориолиса:

1.  По правилу векторного произведения (рис. 3) 

 

  .

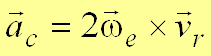
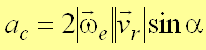Теорема_кориолиса Пусть точка совершает сложное движение: движется относительно неинерциальной системы отсчёта   со скоростью  ;  система   при этом сама движется относительно инерциальной системы координат  , причём линейная скорость движущегося вместе с ней полюса   равна ,  а угловая скорость системы   равна  .

Тогда абсолютная скорость рассматриваемой точки (то есть её линейная скорость в инерциальной системе координат) будет такой:

 ,  причём   ,

где  — радиус-вектор точки относительно полюса  .  Первые два слагаемых в правой части равенства представляют собойпереносную скорость точки, а последнее — её относительную скорость.

Продифференцируем это равенство по времени:

Найдём значение каждого слагаемого в инерциальной системе координат:

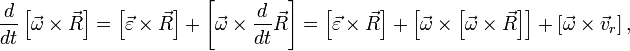
где  — линейное ускорение точки относительно системы ,   — угловое ускорение системы  .

Таким образом, имеем:

Полученное равенство служит математическим выражениемтеоремыКориолиса:  Абсолютное ускорение точки в сложном движении равно геометрической сумме её переносного ускорения (сумма первых трёх слагаемых в правой части),относительного ускорения (четвёртое слагаемое) и добавочного кориолисова ускорения (последнее слагаемое), равного   .

Используя обозначения и , получим запись теоремы Кориолиса в более сжатом виде:

Причиной возникновения кориолисова ускорения является взаимное влияние друг на друга переносного и относительного движений.

Сам Кориолис выражал в 1835 г. свои результаты в иной форме, вводя в рассмотрение переносную и кориолисову силы инерции; общепринятая же ныне чисто кинематическая формулировка теоремы Кориолиса предложена в 1862 г. Анри ЭмеРезалем^[12].

Заметим, что если система   также является неинерциальной и движется относительно другой системы, а та другая относительно следующей и т. д., то величины  ,  для системы   в последнем уравнении следует считать полными — то есть как сумму собственных ускорений (скоростей) всех систем координат (каждой относительно предыдущей), начиная с первой подвижной системы, а  — абсолютным ускорением поступательного движения   относительно неподвижной инерциальной системы координат.

Заметим также, что в частности, чтобы точка относительно неинерциальной системы отсчёта двигалась прямолинейно по радиусу к оси вращения (см. рис.), необходимо приложить к ней силу, которая будет противодействующей суммы Кориолисовойсилы  , переносной вращательной силы  и переносной силы инерции поступательного движения системы отсчёта  . Составляющая же ускорения  не отклонит тело от этой прямой, так как являетсяосестремительным переносным ускорением и всегда направлена по этой прямой. Действительно, если рассматривать уравнение такого движения, то после компенсации в нём вышеупомянутых сил получится уравнение , которое если умножить векторно на , то с учетом  получим относительно дифференциальное уравнение 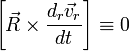, имеющее при любых  и  общим решением , которое и является уравнением такой прямой —  .