31 Условия и уровнения пространственной системы сил

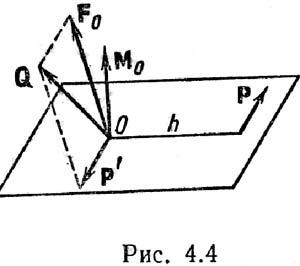
Для равновесия пространственной системы сил необходимо и достаточно, чтобы главный вектор и главный момент этой системы равнялись нулю.Достаточность: при F_o=0 система сходящихся сил, приложенных в центре при­ведения О, эквивалентна нулю, а при М_о=0 система пар сил эквивалентна нулю. Следовательно, исходная система сил эквива­лентна нулю.Необходимость:Пусть данная система сил эквивалентна нулю. Приведя систему к двум силам, заметим, что система сил Q и Р (рис. 4.4) должна быть эк­вивалентна нулю, следовательно, эти две силы должны иметь общую линию действия и должно выполняться рав-во Q=–Р. Но это может быть, если линия действия силы Р проходит через точку О, т. е. если h=0. А это значит, что главный момент равен нулю (М_о=0). Т.к. Q+Р=0, a Q=F_o+P', то F_o+P'+P=0, и, следовательно, F_o= 0. Необх и достуслравновпро­странственнойсист сил им вид: F_o=0, M_o=0 (4.15),

или,  в проекциях на  координатные оси, Fox=åF_kx=F_1x+F_2x+…+F_nx=0; F_Oy=åF_ky=F_1y+F_2y+...+F_ny=0; F_oz=åF_kz=F_1z+F_2z+…+F_nz=0 (4.16).   M_Ox=åM_Ox(F_k)=M_Ox(F₁)+М_ox(F₂)+...+M_Ox(F_n)=0, M_Oy=åM_Oy(F_k)=M_oy(F₁)+M_oy(F₂)+…+M_oy(F_n)=0, М_oz=åМ_Оz(F_k)=М_Оz(F₁)+M_oz(F₂)+...+М_oz(F_n)=0. (4.17)

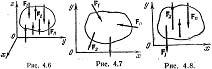
Т.о. при решении задач имея 6 ур-ий можно найти 6 неизвестных. Замечание: пару сил нельзя привести к равнодействующей.Частные случаи: 1) Равновесие пространственной системы параллельных сил. Пусть ось Z параллельна линиям действ силы (рис 4.6), тогда проекции сил на x и y равны 0 (F_kx=0 и F_ky=0), а остаётся только F_oz. А что касается моментов, то остаются только M_oxи M_oy, а M_ozотсутствует. 2) Равновесие плоской системы сил. Остаются ур-я F_ox, F_oyи момент M_oz(рис 4.7). 3) Равновесие плоской системы параллельных сил. (рис. 4.8). Остаются только 2 ур-я: F_oyи M_oz.При составлении ур-ий равновесия за центр привидения может быть выбрана любая точка.

Если система сил находится в равновесии, то ее главный вектор и главный момент равны нулю:

Эти векторные равенства приводят к следующим шести скалярным равенствам:

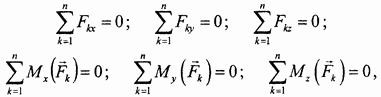
которые называются условиями равновесия пространственной произвольной системы сил.

32 теорема Вариньона, согласно которой моментравнодействующей системы сил относительно какого-либо центра равен геометрической сумме моментов составляющих систему сил относительно того же центра.

Рисунок 1.17

    Например, момент силы F  относительно точки  O можно определить как алгебраическую сумму моментов сил F_x  и  F_y (на которые можно разложить силу F ) относительно той же точки O  (рисунок 1.17). То есть

 M_o(F)= -Fh = -F_x y+ F_y x,  (1.8)

где  F_x , F_y ,  x и y  – проекции на оси координат силы F и радиуса-вектора r .

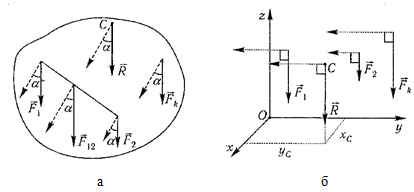
33Центр параллельных сил

Рассмотрим систему параллельных сил  {F1, F2, ..., Fn}. При повороте всех сил системы на один и тот же угол линия действия равнодействующей системы параллельных сил повернется в ту же сторону на тот же угол вокруг некоторой точки (рисунок 1.5, а). Эта точка называется центром параллельных сил. Согласно теореме Вариньона, если система сил имеет равнодействующую, то ее момент относительно любого центра (оси) равен сумме моментов всех сил системы относительно того же центра (оси). Рисунок 1.5 Для определения координат центра параллельных сил воспользуемся этой теоремой. Относительно оси x Mx(R) = ΣMx(Fk),  -yCR= ΣykFkиyC = ΣykFk /ΣFk. Относительно оси y  My(R) = ΣMy(Fk),     -xCR = ΣxkFkиxC = ΣxkFk /ΣFk. Чтобы определить координату  zC, повернем все силы на 90° так, чтобы они стали параллельны осиy(рисунок 1.5, б). Тогда  Mz(R) = ΣMz(Fk),      -zCR = ΣzkFkиzC = ΣzkFk /ΣFk. Следовательно, формула для определения радиус-вектора центра параллельных сил принимает вид  rC = ΣrkFk /ΣFk. Свойства центра параллельных сил: 1 Сумма моментов всех сил  Fkотносительно точкиCравна нулюΣMC(Fk) = 0. 2 Если все силы повернуть на некоторый угол  α, не меняя точек приложения сил, то центр новой системы параллельных сил будет той же точкойC.

34 Центром тяжести твердого тела называется геометрическая точка, жестко связанная с этим телом, и являющаяся центром параллельных сил тяжести, приложенных к отдельным элементарным частицам тела (рисунок 1.6).

Радиус-вектор этой точки

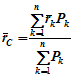
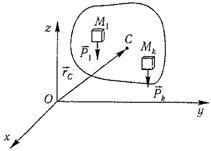
Рисунок 1.6

Для однородного тела положение центра тяжести тела не зависит от материала, а определяется геометрической формой тела.

Если удельный вес однородного тела  γ, вес элементарной частицы тела 

P_k = γΔV_k  (P ₌ γV) подставить в формулу для определения  r_C, имеем

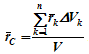
Откуда, проецируя на оси и переходя к пределу, получаем координаты центра тяжести однородного объема

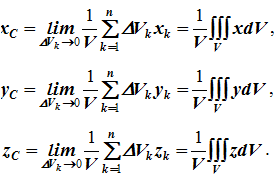
Аналогично для координат центра тяжести однородной поверхности площадью S  (рисунок 1.7, а)

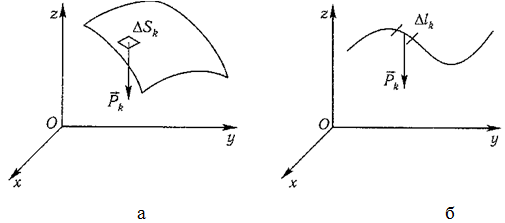
Рисунок 1.7

Для координат центра тяжести однородной линии длиной L  (рисунок 1.7, б)

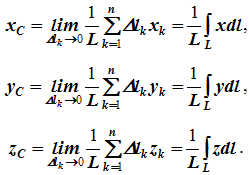
35На каждую частицу тела, находящегося вблизи поверхности Земли, действует направленная вертикально вниз сила, которая называется силой тяжести. Силы тяжести каждой частицы тела, строго говоря, направлены по радиусам к центру Земли и не являются параллельными. Но для тел, размеры которых малы по сравнению с размерами Земли, непараллельность настолько незначительна, что в расчетах с большой точностью силы тяжести их частиц можно считать параллельными, сохраняющими свои значения, точки приложения и параллельность при любых поворотах тела. Поэтому, обозначив силу тяжести частицы через Рк , можно, согласно

формулам  и 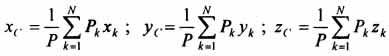, найти точку С, которая неизменно связана с телом и называется центром системы параллельных сил тяжести. Таким образом, центром тяжести твердого тела называется центр системы параллельных сил тяжести частиц данного тела. Точка С — это геометрическая точка, она может и не принадлежать телу, но она всегда с ним связана, например центр тяжести баскетбольного мяча, кольца и др. Выразим силу тяжести (вес) частицы тела через ее объем V. Тогда величина  называется удельным весом, а величина  - плотностью тела в данной точке. ("гамма"-Н/м3) ("ро"-Н*с2/м4)

Методы нахождения центра тяжести.

1) Метод симметрии.

Покажем, что если однородное тело имеет плоскость, ось или центр материальной симметрии, то его центр тяжести находится соответственно в плоскости, на оси или в центре симметрии.

а. Пусть тело симметрично относительно плоскости Оху

Тогда вследствие симметрии каждому элементу К тела объемом (, , ) будет соответствовать элемент К' того же объема с координатами (, ,-). Поэтому статический момент объема  и координата 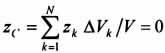. Следовательно, центр тяжести тела будет лежать в плоскости симметрии Оху.

б. Пусть тело симметрично относительно оси Oz.

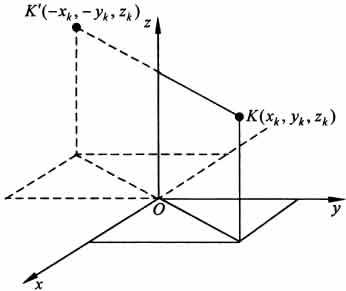
Тогда всякому элементу К тела объемом  с координатами (, , ) будет соответствовать такой же по объему элемент К', расположенный симметрично относительно оси Oz и имеющий координаты (-,- , ). Поэтому статические моменты и, следовательно, координаты 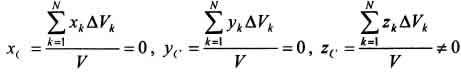. Таким образом, центр тяжести будет находится на оси симметрии.

в. Пусть тело имеет центр симметрии, который примем за начало координат. Тогда всякой частице тела объемом , определяемой радиус-вектором rк, будет соответствовать частица такого же объема с радиус-вектором (-rк), симметричная ей относительно центра О. Поэтому . Следовательно, центр тяжести будет находиться в центре симметрии. Например, центры тяжести однородных куба, сферы, кольца, прямоугольной или круглой пластины лежат в геометрическом центре этих тел.

2) Метод разбиения.

Этот метод основан на применении формул 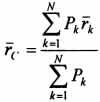 и 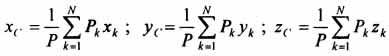. Его используют, когда тело можно разбить на ряд частей, центры тяжести которых известны из условий симметрии. Метод разбиения можно наглядно проиллюстрировать с помощью рисунка.

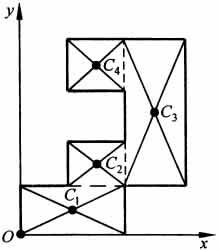
Расположив тело в системе координат, разделив его мысленно на отдельные части, веса которых Р1, Р2, Р3, Р4, а центры тяжести известны, вычислим вес тела и, согласно формулам , координаты центра тяжести С всего тела. Если тело имеет вырез, причем известны центр тяжести тела без выреза и центр тяжести вырезанного тела, то для определения координат центра тяжести используют метод отрицательных масс (частный случай метода разбиения).

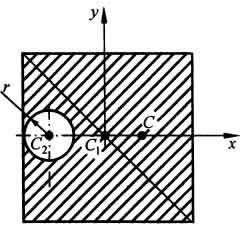
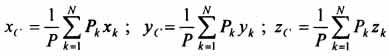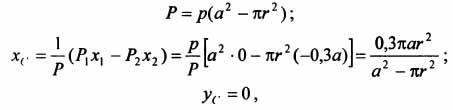На рисунке изображена квадратная пластина, сторона которой а. В пластине выполнено круглое отверстие с радиусом r=0,2а и координатами центра x2=-0,3а; у2=0. Координаты центра тяжести С, пластины без отверстия x1=0, у1=0. Рассмотрим два тела: пластину без отверстия и диск, соответствующий вырезанному отверстию. При использовании формул  вес диска будем считать отрицательным. Тогда, где р — вес единицы площади пластины.