Предельная относительная погрешность приближения а* определяется отношением δ (a*)= (aa** ). Отсюда получается часто используемое соотно-

шение:

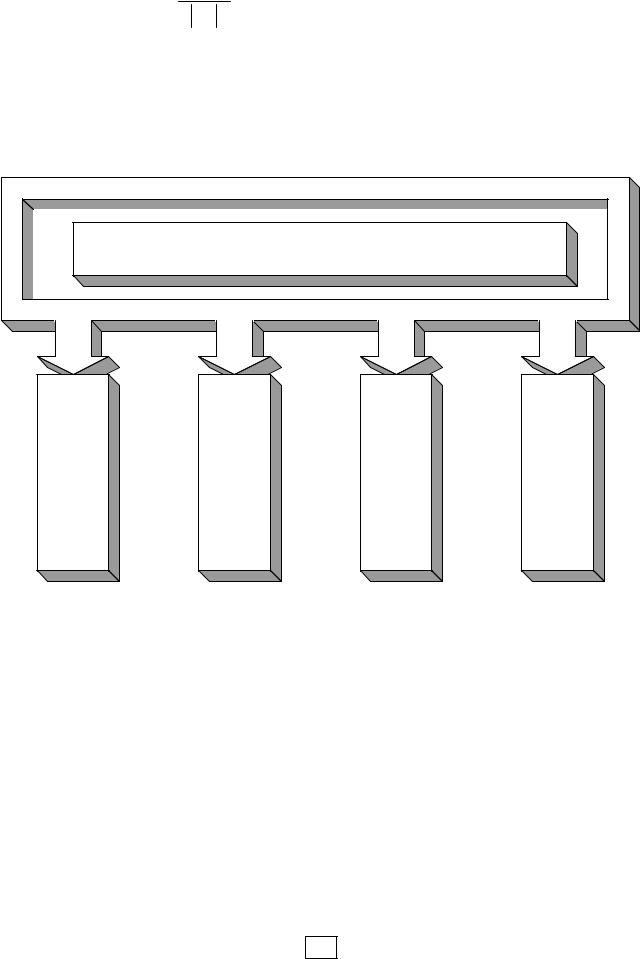
Структура погрешности

Есть четыре источника погрешности результата: математическая модель, исходные данные, приближенный метод и округления при вычислениях

(рис. 2.2).

Рис. 2.2 Структура погрешности результата численного решения

Один из типов погрешностей обусловлен неадекватностью выбранной математической модели исходной физической. Эта неадекватность в большей или меньшей степени присуща всем приближенно решаемым задачам. Данная погрешность является неустранимой, и она определяется на восьмом этапе решения задачи (см. рис. 1.1). Остальные три типа погрешностей являются сугубо вычислительными и обусловлены следующими причинами.

Исходные данные зачастую неточны; например, это могут быть экспериментально измеренные величины. Так, например, в прецизионных физических измерениях точность доходит до 10-12, но уже характерная астрономическая и геодезическая точность равна 10-6, а во многих физических и технических задачах погрешность измерения бывает 1 – 10%. Погрешность исходных данных

19

δ x приводит к так называемой неустранимой (она не зависит от математика) погрешности решения δ y = A(x +δ x)− A(x).

Если устранить неопределенность в исходных данных, например, путем их фиксирования и найти решение с помощью какого-либо численного метода, то получится результат, не в точности соответствующий исходным данным. Это есть погрешность численного или какого-либо другого приближенного метода (например, приближенно-аналитического); именно такие погрешности будут оцениваться при рассмотрении численных методов. Эти оценки могут получаться до выполнения вычислений (априорные оценки) и после них (апостериорные оценки).

Погрешность метода связана с тем, что точные оператор и исходные данные заменяются приближенными. Например, заменяют интеграл суммой, производную – разностью, функцию – многочленом или строят бесконечный итерационный процесс и обрывают его после конечного числа итераций. Методы строятся обычно так, что в них входит некоторый параметр; при стремлении параметра к определенному пределу погрешность метода стремится к нулю, так что эту погрешность можно регулировать.

Погрешность метода целесообразно выбирать так, чтобы она была в 2–5 раз меньше неустранимой погрешности. Большая погрешность метода снижает точность ответа, а заметно меньшая – невыгодна, ибо это обычно требует значительного увеличения объема вычислений.

Вычисления, как на бумаге, так и на ЭВМ выполняют с определенным числом значащих цифр. Это вносит в ответ погрешность округления, которая накапливается в ходе вычислений.

Компьютерное представление действительных чисел ограничено фиксированной точностью мантиссы. Истинное значение не всегда точно сохраняется в компьютерном представлении. Фактически число, которое хранится в компьютере, может усекаться или содержать округленную последнюю цифру. Таким образом, поскольку диск компьютера работает только с ограниченным количеством цифр в машинных числах, вводится ошибка округления и распространяется на последующие вычисления.

При решении больших задач выполняются миллиарды действий. Казалось бы, начальные ошибки возрастут в 109 раз, и погрешность ответа будет огромной. Однако при отдельных действиях фактические погрешности чисел могут иметь разные знаки и компенсировать друг друга. Согласно статистике при N одинаковых действиях среднее значение суммарной ошибки превышает еди-

ничную примерно в N раз, а вероятность заметного уклонения суммарной ошибки от среднего значения очень мала. Следовательно, если нет систематических причин, то случайное накопление ошибок не слишком существенно.

Отметим, что в большинстве прикладных задач неприятностей можно избежать, проводя расчет с двойной или тройной точностью. Такая возможность реализована в хороших математических обеспечениях ЭВМ; это в несколько раз увеличивает время расчета, зато позволяет пользоваться уже известными алгоритмами, а не разрабатывать новые.

20

При любых расчетах справедливо правило: надо удерживать столько значащих цифр, чтобы погрешность округления была существенно меньше всех остальных погрешностей.

Значащие цифры

Значащими цифрами приближенного числа называют все цифры в его записи, начиная с первой ненулевой слева.

Первые п значащих цифр приближенного числа называются верными, если абсолютная погрешность этого числа не превышает половины единицы разряда, соответствующего п-й значащей цифре, считая слева направо. Излишние сохраненные цифры, помимо верных, называются сомнительными.

Вычислить приближенное число с точностью ε = 10−n означает, что необходимо сохранить верной значащую цифру, стоящую в п-м разряде после запятой.

На практике возникает необходимость в округлении приближенного числа, т.е. замене его числом с меньшим количеством значащих цифр. Для округления числа до п значащих цифр следует отбросить все его цифры, стоящие справа от п-й значащей цифры. При этом:

а) если первая из отброшенных цифр меньше 5 , то оставшиеся десятичные знаки сохраняются без изменения;

б) если первая из отброшенных цифр больше 5 либо равна 5 и среди остальных отброшенных цифр есть ненулевые, то к последней оставшейся цифре прибавляется единица;

в) если первая из отброшенных цифр равна 5 и остальные отброшенные цифры нулевые, то последняя оставшаяся цифра не изменяется, если она четная, и увеличивается на единицу, если она нечетная.

Абсолютная и относительная погрешности записываются в виде чисел с одной или двумя значащими цифрами, и они округляются с избытком. В записи приближенных чисел они указываются так:

ность половины единицы (1/2 ед.) младшего разряда. Так, для а=5,63 абсолютная погрешность = 0,005 .

Распространение ошибки

Рассмотрим, как ошибка может распространиться в последующих вычислениях. Рассмотрим сложение двух чисел р и q (истинные значения) с приближенными значениями р* и q*, которые содержат соответственно ошибки εp и

Следовательно, для сложения ошибка суммы равна сумме ошибок слагаемых.

Распространение ошибки в умножении более сложно. Произведение равно:

21

Отсюда, если р и q больше 1 по абсолютной величине, то члены p* εq и q* εp показывают, что, возможно, происходит увеличение первоначальных ошибок εp и εq . Это становится понятно, если посмотреть на относительную ошибку. Перегруппировав члены в (2.15), получаем:

относительным ошибкам при приближениях р* и q*). Затем, произведя эти замены в (2.17), получим простое соотношение:

Это показывает, что относительная ошибка произведения pq приближенно равна сумме относительных ошибок приближений p* и q* .

Единицы измерения информации

При записи и обработке информации на компьютере, количество информации измеряется в байтах и битах.

Бит (англ. bit, от binary – двоичный и digit – знак), наименьшая единица количества информации, двоичная единица. Бит в вычислительной технике – двоичная цифра, двоичный разряд. Число бит памяти ЭВМ определяет максимальное количество двоичных цифр, вмещаемых ею; число бит данных есть количество двоичных разрядов, в которых они записаны. Более крупные единицы измерения: килобит (1 Кбит = 210 бит = 1024 бит), мегабит (1 Мбит = 220

бит = 1048576 бит).

Байт (англ. byte), единица измерения количества информации при ее хранении, передаче и обработке на ЭВМ. Состоит из 8 бит (двоичных единиц). Информация, содержащаяся в одном байте обычно достаточна для представления одной буквы, цифры, знака препинания или 2 десятичных цифр. Более крупные единицы измерения: килобайт (1 Кбайт = 210 байт = 1024 байта), мегабайт (1 Мбайт = 1024 Кбайт = 220 байт = 1048576 байт), гигабайт (1 Гбайт = 1024 Мбайт = 230 байт = 1073741824 байт).

22