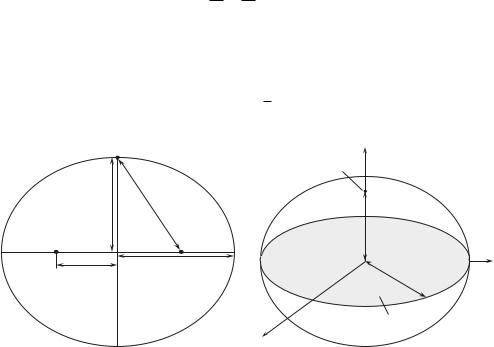
1. Системи координат в геодезiї

1.1. Геометричнi властивостi елiпса та сфероїда

Задачею вищої геодезiї є вивчення фiгури та зовнiшнього гравiтацiйного поля Землi. Пiд фiгурою Землi розумiють фiзичну поверхню суходолу у сполученнi з незбуреною поверхнею Свiтового океану. Наближенням фiгури Землi є поверхня геоїда, тобто поверхня, яка спiвпадає iз незбуреною (припливами, вiтром, коливанням тиску) поверхнею води Свiтового океану та уявно продовжується пiд материки таким чином, що напрями лiнiй виска всюди перетинають цю поверхню пiд прямим кутом. Форма геоїда досить складна внаслiдок неоднорiдностi розподiлу мас всерединi Землi, а тому використовувати цю поверхню при математичному розв’язаннi геодезичних задач дуже незручно. Тому при розв’язаннi задач вищої геодезiї фiгура Землi замiнюється бiльш простою з математичної точки зору поверхнею — елiпсоїдом обертання або, iншими словами, сфероїдом. Ця поверхня утворюється шляхом обертанням елiпса навколо малої осi. Елiпс є алгебраїчною кривою 2-го порядку i описується рiвнянням

нами a, b, α, e, e′:

p p e p

b = a(1−α) = a 1−e2, e = 2α−α2, e′ = √1−e2 , α = 1− 1−e2. (1.6)

Точки F1, F2 на рис. 1.1, розташованi на великiй осi елiпса на вiдстанi ae вiд його центру, називаються фокусами. Основною геометричною властивiстю елiпса є те, що сума вiдстаней вiд будь-якої точки елiпса до його фокусiв дорiвнює 2a.

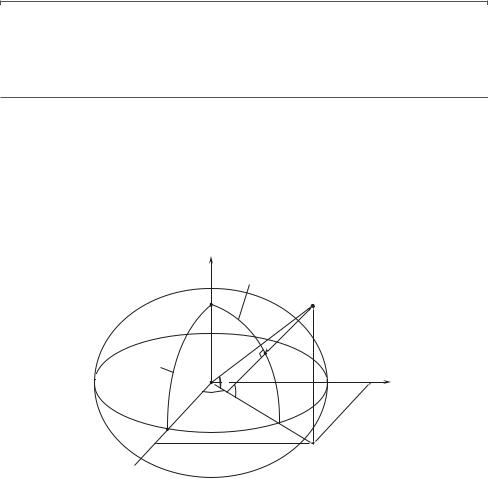
Обертаючи елiпс навколо осi b, отримаємо сфероїд (рис. 1.2). Його рiвняння буде

Величина a для земного сфероїда називається екваторiальним радiусом. При вiдомих значеннях a i b площа елiпса S та об’єм сфероїда V вира-

1.2. Характеристика загальноземних систем координат

Елiпсоїд обертання (сфероїд), який представляє земну поверхню, в геодезiї називають просто елiпсоїдом. Його пiдбирають таким чином, щоб вiн був близьким до фiгури Землi в цiлому. Такий елiпсоїд називають загальноземним; його вибирають так, щоб центр елiпсоїда спiвпадав з центром мас Землi, його екваторiальна площина спiвпадала з площиною земного екватора, вiсь симетрiї спiвпадала з вiссю обертання Землi, а сума квадратiв вiдхилень по висотi вiд поверхнi геоїда була мiнiмальною.

Для окремих країн вводять елiпсоїди, отриманi на основi геодезичних вимiрювань, що охоплюють територiю даної країни. Такi елiпсоїди називають референц-елiпсоїдами. Референц-елiпсоїд призначений для наближеного описання не всiєї поверхнi Землi, а лише певної її дiлянки. Референц-

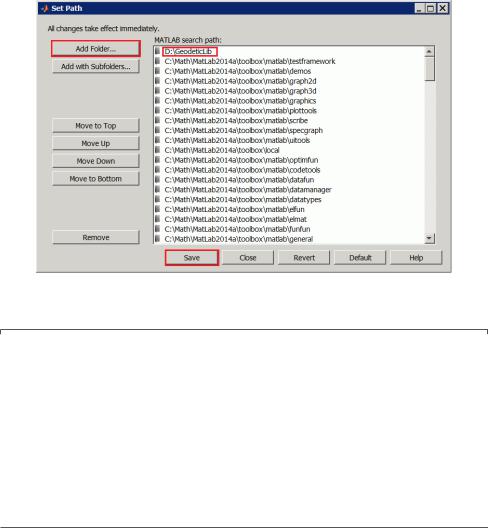
Рис. 1.3

>> WGS84 WGS84 =

a:6378137

b:6356752.314245 alpha: 0.00335281066474748

e:0.081819190842622

w:7.292115e-05 GM: 398600441800000

J2: 0.0010826298213133 Uo: 62636851.7146

g_pol: 9.8321849378 g_eq: 9.7803253359

m:0.00344978650684

Поля цiєї структури мають наступне трактування: a, b — велика i мала пiвосi елiпсоїда, м;

alpha, e — стиснення та ексцентриситет елiпсоїда;

w— кутова швидкiсть обертання Землi, рад/с;

GM — добуток гравiтацiйної сталої на масу Землi, м3/с2; J2 — коефiцiєнт другої зональної гармонiки;

Uo — нормальний потенцiал на поверхнi елiпсоїда, м2/с2; g_pol — прискорення вiльного падiння на полюсi, м/с2; g_eq — прискорення вiльного падiння на екваторi, м/с2.

Цими значеннями можна користуватись при обчисленнях. Нагадаємо, що звернення до полiв структури має формат Iм'яСтруктури.Iм'яПоля. Наприклад, обчислимо об’єм елiпсоїда:

load WGS84_data.mat

V = 4/3 * pi * WGS84.a^2 * WGS84.b;

Для зручностi значення полiв можна спочатку занести в окремi змiннi:

load WGS84_data.mat

V = 4/3 * pi * a^2 * b;

1.3. Деякi кориснi функцiї для MATLAB

Розглянемо деякi функцiї, спецiально написанi для використання при розв’язаннi задач в середовищi MATLAB; m-файли з даними функцiями мiстяться в папцi GeodeticLib.

dms2rad переводить значення кута з формату “градуси, мiнути, секунди” в радiани

Angle = dms2rad(градуси, мiнути, секунди) — це перший варiант виклику функцiї; в якостi аргументiв передаються три числа.

Angle = dms2rad([градуси, мiнути, секунди]) — iнший варiант виклику функцiї; аргумент всього один — вектор з трьох чисел.

Отже, функцiя dms2rad викликається в одному з двох варiантiв, наприклад:

%змiннiй Angle присвоюється значення кута 60◦ 20′ 30,2345′′,

%виражене в радiанах

Angle = dms2rad( 60, 20, 30.2345 );

Angle = dms2rad([60, 20, 30.2345]);

% в результатi Angle = 1.05316189636233

rad2dms виконує обернену задачу: на основi значення радiанної мiри кута повертає вектор з трьох елементiв у виглядi

[градуси, мiнути, секунди]. Наприклад, в результатi такого виклику

Angle_deg = rad2dms(1.05316189636233);

змiннiй Angle_deg присвоюється вектор [60, 20, 30.2345].

rad2str на основi кута, вираженого в радiанах, повертає символьний рядок вигляду градуси◦ мiнути′ секунди′′; цю функцiю доцiльно використовувати при видачi значення кута в командне вiкно.

Angle =

1.05316189636233

Angle =

Angle =

60° 20' 30.2345"

1.4.Геоцентричнi декартовi, сферичнi та геодезичнi елiпсоїдальнi координати

Система координат, початок якої знаходиться в центрi мас Землi або близько нього, називається геоцентричною чи квазiгеоцентричною вiдповiдно. Тому координати, зв’язанi з загальноземним елiпсоїдом, називаються загальноземними i геоцентричними, а координати, зв’язанi з вибраним референц-елiпсоїдом, — референцними i квазiгеоцентричними.

R

X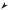

Рис. 1.4. Зображено вiсi системи геоцентричних декартових координат, довгота L, геоцентрична широта ϕ, геодезична широта B.

Декартовi координати X,Y , Z вводять таким чином, щоб початок координат O збiгався з центром вибраного елiпсоїда (загальноземного або референц-елiпсоїда), вiсь Z була направлена вздовж вiсi симетрiї елiпсоїда, а вiсi X та Y лежали в екваторiальнiй площинi елiпсоїда. Меридiан, який проходить через точку перетину вiсi X та екватору елiпсоїда (точка R на рис. 1.4), приймається за початковий.

Положення точки Q в просторi можуть задавати також сферичнi координати: довгота L — це двогранний кут мiж площиною початкового меридiану та площиною меридiану точки Q (лежить в межах −180◦ < L 6 +180◦

або 0◦ 6 L < 360◦), геоцентрична широта ϕ — кут мiж радiус-вектором точки Q та екваторiальною площиною елiпсоїда (−90◦ 6 ϕ 6 +90◦), а також вiдстань r точки Q вiд початку координат (на рис. 1.4 це довжина вiдрiзка

OQ).

Зв’язок мiж координатами X,Y , Z та r, L, ϕ виражається формулами

X = r cos L cos ϕ

Z = r sin ϕ

Обернений перехiд вiд X,Y , Z до r, L, ϕ в лiтературi традицiйно записується в формi

arctg, а функцiєю atan2, яка є в рiзних математичних пакетах. Вона повертає виражене в радiанах значення кута мiж вiссю x i напрямком на точку площини з координатами (x, y). Цей кут вiдраховується вiд вiсi x проти годинникової стрiлки, а його значення лежить в межах вiд −π до +π.

В системi MATLAB функцiя atan2 має формат виклику

p = atan2(y,x)

та повертає виражене в радiанах значення кута мiж вiссю x i напрямком на точку площини з координатами (x, y). Цей кут вiдраховується вiд вiсi x проти годинникової стрiлки, а його значення лежить в межах вiд −π до +π. Отже, функцiя atan2(y,x) є нiби “вдосконаленим” варiантом виклику atan(y/x). Вона повертає коректне значення кута навiть при x = 0.

На рис. 1.5 зображено кут α, який визначає напрямок на точку A з координатами (x, y). Очевидно, значення кута α не змiниться, якщо кожну

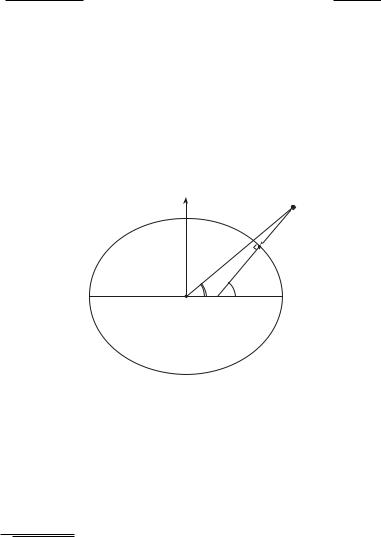
В геодезичних елiпсоїдальних координатах замiсть геоцентричної широти ϕ використовується геодезична широта B — це кут мiж проведеною з точки Q нормаллю (перпендикуляром) до поверхнi елiпсоїда та екваторiальною площиною (−90◦ 6 B 6 +90◦). На рис. 1.6 показано вiдмiннiсть мiж геоцентричною та геодезичною широтами. Висота H — це вiдстань мiж точкою Q та поверхнею елiпсоїда вздовж нормалi (на рис. 1.4 висота H дорiвнює довжинi вiдрiзка SQ). Нарештi, довгота L має той самий змiст, що i в системi сферичних координат.

Рис. 1.6. Геоцентрична широта ϕ та геодезична широта B

Формули переходу вiд декартових координат X,Y , Z до геодезичних координат B, L, H вiдносно земного елiпсоїда з параметрами a, e мають такий вигляд:

(1.9)

де N = p a

1−e2 sin2 B

Для зворотного переходу вiд X,Y , Z до B, L, H iснують такi формули: