Вища геодезія

6.4.1.Числовий приклад розв’язання оберненої геодезичної задачi на малi вiдстанi за формулами з середнiми аргументами

Розв’яжемо обернену геодезичну задачу для двох пунктiв на елiпсоїдi WGS-84:

Розв’язання. Послiдовно знаходимо

b = B2 −B1 = 0,0523598775598298 рад,

l= L2 −L1 = 0,0698131700797733 рад,

Bm = 12 (B1 + B2) = 0,89884456477708, k = 0,0029851314363139,

p = 0,00261171992217719, Q = 333596,111115292,

P = 277757,985960503,

h = 0,0546637345267999,

s= 434092 м,

Am = 0,694315714303351,

A1 = 0,666983847039952 рад = 38◦ 12′ 55,2940′′,

A2 = 3,86324023515654 рад = 221◦ 20′ 50,4986′′.

6.5.Функцiї для розв’язання прямої та оберненої геодезичної задачi на елiпсоїдi

Описанi вище алгоритми розв’язання прямої та оберненої геодезичних задач дають наближенi результати i придатнi лише для задач на малi вiдстанi, але iснують алгоритми, якi дозволяють розв’язувати геодезичнi задачi на елiпсоїдi досить точно, принаймнi з похибкою менше вiд 1 мм при довiльних вiдстанях на поверхнi елiпсоїда. Цi алгоритми реалiзованi у ви-

глядi функцiй SolveDirectProblem та SolveInverseProblem.

SolveDirectProblem розв’язує пряму геодезичну задачу на поверхнi елiпсоїда. Формат виклику:

[B2, L2, A2] = SolveDirectProblem(B1, L1, A1, s, a, e)

Дана функцiя на основi координат B1, L1 початкової точки геодезичної лiнiї та її довжини s обчислює та повертає геодезичнi координати B2, L2 кiнцевої точки геодезичної лiнiї, а також прямий азимут A2 в кiнцевiй точцi геодезичної лiнiї. Довжина геодезичної s має задаватися в тих самих одиницях, що i велика пiввiсь a елiпсоїда. Всi кути B1, L1, A1, B2, L2, A2 виражаються в радiанах.

Для прикладу знайдемо розв’язок прямої геодезичної задачi з п.6.1.1

clc, clear

load WGS84_data

B1 = dms2rad(50, 0, 0);

L1 = dms2rad(60, 0, 0);

A1 = dms2rad(45, 0, 0);

s= 50000;

[B2, L2, A2] = SolveDirectProblem(B1, L1, A1, s, WGS84.a, WGS84.e);

Disp( ' B2 = ' , rad2str(B2,4))

Disp( ' L2 = ' , rad2str(L2,4))

Disp( ' A2 = ' , rad2str(A2,4))

В результатi

B2 =

50° 19' 0.4638"

L2 =

60° 29' 47.0429"

A2 =

45° 22' 52.1335"

SolveInverseProblem розв’язує обернену геодезичну задачу на поверхнi елiпсоїда. Формат виклику:

[A1, A2, s] = SolveInverseProblem(B1, L1, B2, L2, a, e)

Ця функцiя на основi координат B1, L1, B2, L2 початкової та кiнцевої точок геодезичної лiнiї повертає прямий азимут A1 в початковiй точцi геодезичної лiнiї, обернений азимут A2 в кiнцевiй точцi, а також довжину s геодезичної лiнiї. Всi кути B1, L1, B2, L2, A1, A2 виражаються в радiанах. Значення кутiв A1, A2 лежать в межах вiд 0 до 2π.

Знайдемо розв’язок оберненої геодезичної задачi з п.6.4.1

clc, clear

load WGS84_data

B1 = dms2rad(50, 0, 0);

L1 = dms2rad(60, 0, 0);

B2 = dms2rad(53, 0, 0);

L2 = dms2rad(64, 0, 0);

[A1,A2,s] = SolveInverseProblem(B1, L1, B2, L2, WGS84.a, WGS84.e); Disp( ' A1 = ' , rad2str(A1, 4))

Disp( ' A2 = ' , rad2str(A2, 4)) Disp( ' s = ' , s)

В результатi

A1 =

38° 12' 55.2920"

A2 =

221° 20' 50.4964"

s=

434091.961033995

6.6.Розв’язання сфероїдичного трикутника при вiдомому положеннi вершин

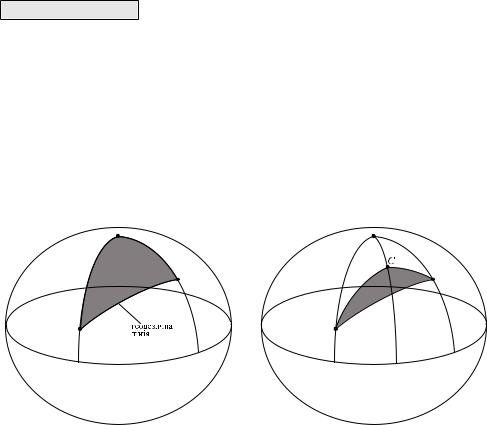
Нехай в сфероїдичному трикутнику (рис. 6.2) вiдомi координати вершин (B1, L1), (B2, L2), (B3, L3). Для знаходження кутiв та довжин сторiн трикутника спочатку необхiдно розв’язати три оберненi геодезичнi задачi: мiж вершинами 1 та 2, мiж вершинами 2 та 3, а також мiж вершинами 1 та 3. В результатi розв’язання цих задач будуть отриманi значення довжин сторiн s12, s23 та s13, а також азимутiв A12, A21, A23, A32, A13, A31.

P

A23

2 s23

3

A12

A13 s13

1

Рис. 6.2

Шуканi кути трикутника, очевидно, виражаються виражаються через азимути наступним чином:

Формули (6.2) виписанi для трикутника, зображеного на рис. 6.2. Для загального випадку, коли вершини трикутника розташованi по-iншому, а деякi з азимутiв мають вiд’ємнi значення, обчисленi за формулами (5.36) кути

Особливiстю функцiї AreaAboveGeodesic є те, що вона повертає додатне значення площi, якщо L2 > L1 та вiд’ємне, якщо L2 < L1. Цю властивiсть можна використати для обчислення площi сфероїдичного трикутникаABC, зображеного на рис. 6.4. Очевидно, його площа буде виражатись через площi полярних трикутникiв наступним чином:

S ABC = S PAB −S PCB −S PAC

Але функцiя AreaAboveGeodesic дозволяє обчислити площу трикутникаABC просто як алгебраїчну суму додатних та вiд’ємних площ, не зважаючи на те, як само розташованi вершини на елiпсоїдi. Нехай вершина A має координати B1, L1; вершина B — координати B2, L2; вершина C — координати B3, L3. Тодi площа трикутника ABC обчислюється як

S = AreaAboveGeodesic(B1, L1, B2, L2, a, e) + ...

AreaAboveGeodesic(B2, L2, B3, L3, a, e) + ...

AreaAboveGeodesic(B3, L3, B1, L1, a, e)

Важливо лише, щоб координати вершин, якi передаються до функцiї AreaAboveGeodesic, утворювали циклiчну послiдовнiсть (B1, L1) → (B2, L2) → (B3, L3) → (B1, L1), тобто здiйснювався “обхiд” трикутника ABC вздовж сторiн проти годинникової стрiлки.

7.Плоскi прямокутнi координати Гауса–Крюгера

Врядi випадкiв розв’язання прямої i оберненої геодезичних задач на поверхнi сфероїда проводиться мiж точками, якi вiддаленi одна вiд одної на вiдстанi, малi порiвняно з розмiрами самого сфероїда. В таких випадках набагато простiше спроектувати дiлянку поверхнi сфероїда на площину та використовувати для розв’язання геодезичних задач формули плоскої тригонометрiї. При будь-якому зображеннi поверхнi сфероїда на площинi змiнюється взаємне положення точок, тобто виникають спотворення довжин лiнiй, кутiв та площ. Якщо в математичнiй картографiї на площинi зображують великi областi земної поверхнi, то в геодезiї використовують зображення вiдносно невеликої частини поверхнi земного сфероїда. Це обумовлено наступною вимогою: спотворення лiнiйних i кутових величин при перенесеннi їх з поверхнi сфероїда на площину повиннi бути мiнiмальними.

З усiєї множини картографiчних проекцiй в геодезiї використовують лише конформнi проекцiї. В конформних проекцiях кути мiж лiнiями на криволiнiйнiй поверхнi при зображеннi цих лiнiй на площинi не змiнюються, а масштаб в данiй точцi зображення не залежить вiд напрямку.

7.1.Умови конформного вiдображення поверхнi сфероїда на площинi

Пiд вiдображенням однiєї поверхнi на iншу розумiють взаємно однозначну точкову вiдповiднiсть мiж поверхнями, за яким кожнiй точцi однiєї поверхнi ставиться у вiдповiднiсть в якостi зображення деяка точка iншої поверхнi.

Для отримання вiдображення поверхнi сфероїда на площину потрiбно задати залежнiсть мiж геодезичними координатами B, L точок на сфероїдi та декартовими прямокутними координатами x, y на площинi, тобто задати функцiї

x = x(B, L), y = y(B, L). (7.1) З’ясуємо умови, яким повиннi задовольняти функцiї (7.1), щоб вiдобра-

ження було конформним.

Нехай точка A, яка має координати x, y (рис. 7.1,б) є зображенням на площинi деякої точки A0 з координатами (B, L) на поверхнi сфероїда, точка D — зображенням точки D0 з координатами (B + dB, L), а точка C — зображенням точки C0 з координатами (B, L+ dL). Таким чином, дуга AD є зображенням нескiнченно малої дуги меридiана довжиною M dB, а дуга AC — зображенням нескiнченно малої дуги паралелi довжиною N cos B dL.

по координатi x та координатi y вiдповiдно. Аналогiчно, при перемiщеннi вздовж нескiнченно малої дуги паралелi вiд точки A0 до C0 геодезичнi координати отримують прирости dB = 0 та dL, а зображення перемiщується вiд точки A в точку C, тобто тобто на вiдстанi

звiдки знаходимо умови, яким повиннi задовольняти функцiї (7.1), щоб

якi дозволяють здiйснювати перехiд вiд плоских координат до геодезичних. При конформному вiдображеннi цi функцiї мають задовольняти умовам,

В цьому випадку зближення меридiанiв та масштаб будуть визначатися

7.2. Обчислення координат в проекцiї Гауса–Крюгера

Проекцiя Гауса–Крюгера є конформним вiдображенням поверхнi земного сфероїда на площину з постiйним масштабом на прямолiнiйному зображеннi одного з меридiанiв.

Виберемо на поверхнi сфероїда один з меридiанiв з довготою L0 та зобразимо його на площинi у виглядi прямої, яку приймемо за вiсь x системи плоских декартових координат. Вказаний меридiан буде називатися осьовим. Зображення точки перетину осьового меридiана з екватором — точку O — приймемо за початок плоских координат.

Масштаб зображення осьового меридiану для всiх його точок приймемо рiвним одиницi. Це означає, що дуга осьового меридiану довжиною X вiдображається на площинi у виглядi прямого вiдрiзка такої ж самої довжини.

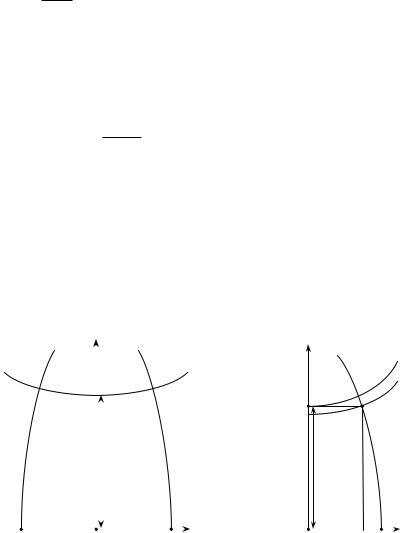
Зобразимо на площинi сегмент поверхнi сфероїда — область вiд полюсу до екватора, обмежену двома меридiанами, довготи яких L1 та L2 вiдрiзняються вiд L0 на величини −l та +l, тобто

L1 = L0 −l, L2 = L0 + l,

причому точки, якi лежать на сфероїдi симметрично вiдносно осьового меридiану, на площинi будуть лежати симметрично вiдносно вiсi x (рис. 7.2). Таким чином, положення будь-якої точки на поверхнi сфероїда будемо характеризувати її геодезичною широтою B та рiзницею довгот l = L − L0 вiдносно осьового меридiану. Перехiд вiд змiнної L до l залишає в силi

X — це довжина дуги меридiану, яка вiдраховується вiд екватору згiдно (4.14)