нами a, b, α, e, e′:

p p e p

b = a(1−α) = a 1−e2, e = 2α−α2, e′ = √1−e2 , α = 1− 1−e2. (1.6)

Точки F1, F2 на рис. 1.1, розташованi на великiй осi елiпса на вiдстанi ae вiд його центру, називаються фокусами. Основною геометричною властивiстю елiпса є те, що сума вiдстаней вiд будь-якої точки елiпса до його фокусiв дорiвнює 2a.

Обертаючи елiпс навколо осi b, отримаємо сфероїд (рис. 1.2). Його рiвняння буде

Величина a для земного сфероїда називається екваторiальним радiусом. При вiдомих значеннях a i b площа елiпса S та об’єм сфероїда V вира-

1.2. Характеристика загальноземних систем координат

Елiпсоїд обертання (сфероїд), який представляє земну поверхню, в геодезiї називають просто елiпсоїдом. Його пiдбирають таким чином, щоб вiн був близьким до фiгури Землi в цiлому. Такий елiпсоїд називають загальноземним; його вибирають так, щоб центр елiпсоїда спiвпадав з центром мас Землi, його екваторiальна площина спiвпадала з площиною земного екватора, вiсь симетрiї спiвпадала з вiссю обертання Землi, а сума квадратiв вiдхилень по висотi вiд поверхнi геоїда була мiнiмальною.

Для окремих країн вводять елiпсоїди, отриманi на основi геодезичних вимiрювань, що охоплюють територiю даної країни. Такi елiпсоїди називають референц-елiпсоїдами. Референц-елiпсоїд призначений для наближеного описання не всiєї поверхнi Землi, а лише певної її дiлянки. Референц-

2

елiпсоїд вiдрiзняється вiд загальноземного елiпсоїда величинами екваторiального радiусу та стиснення, центр референц-елiпсоїда змiщений вiдносно центру мас Землi, але його екваторiальна площина залишається паралельною до екваторiальної площини Землi, а значить мала вiсь референцелiпсоїда паралельна до малої вiсi загальноземного елiпсоїда.

Загальноземнi та референц-елiпсоїди служать координатними поверхнями, вiдносно яких визначаються геодезичнi координати пунктiв, а тому системи координат, якi використовуються в геодезiї, зв’язанi з вiдповiдними їм елiпсоїдами.

На даний час Мiжнародний геодезичний i геофiзичний союз (IUGG

— International Union of Geodesy and Geophysics) в якостi загальноземної геодезичної системи координат використовує систему GRS-80 (Geodetic Reference System, 1980 р.)

Починаючи з 1987 року глобальна система визначення мiсцеположення NAVSTAR GPS використовує як опорну свiтову геодезичну систему WGS– 84 (World Geodetic System, 1984 р.). В нiй параметри елiпсоїда майже збiгаються з параметрами елiпсоїда системи GRS-80, а центр елiпсоїда з точнiстю ±1 м збiгається з центром мас Землi.

Система ГЛОНАСС дiє в координатнiй системi ПЗ–90 (Параметри Землi, 1990 р.).

Додаток А мiстить таблицю, в якiй наведено числовi параметри для деяких загальноземних елiпсоїдiв.

При розв’язаннi геодезичних задач в MATHCAD нам будуть потрiбнi значення геометричних характеристик елiпсоїда WGS–84. Всерединi файла WGS84_data.xmcdz ряду змiнних присвоєно значення характеристик елiпсоїда WGS–84 наступним чином:

3

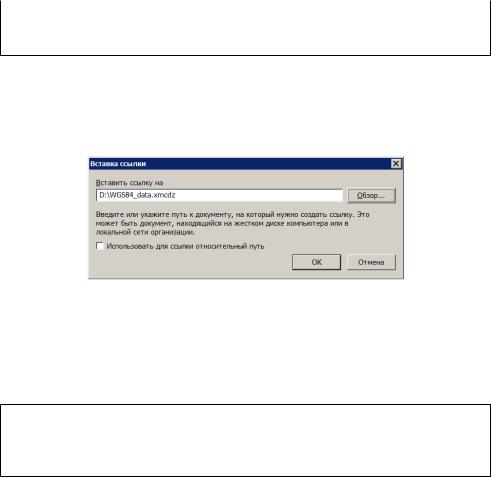
Для того, щоб цi значення були доступнi всерединi MATHCAD - документу, потрiбно на початку документу вставити посилання на файл

WGS84_data.xmcdz. Це робиться через пункт меню Вставка Ссылка. В дiалоговому вiкнi Вставка ссылки (рис. 1.3) потрiбно натиснути кнопку

Обзор, потiм вказати на файл WGS84_data.xmcdz.

Рис. 1.3

Корисно також увiмкнути прапорець Использовать для ссылки относительный путь (вiн стає доступним тiльки пiсля збереження MATHCAD -документу), щоб при перемiщеннi файлiв разом у iншу папку чи на iнший комп’ютер не потрiбно було створювати посилання заново.

Для прикладу обчислимо об’єм елiпсоїда:

ǹ ȣȓȒȈ:D:\WGS84_DATA.XMCD

1.3. Деякi кориснi функцiї для Mathcad

Файл GeodeticLib.xmcdz — це бiблiотека функцiй, якi будуть застосовуватись при розв’язаннi задач в середовищi MATHCAD. Для того, щоб всерединi MATHCAD -документу були доступнi цi функцiї, потрiбно на початку документу вставити посилання на файл GeodeticLib.xmcdz.

Розглянемо призначення поки що двох функцiй.

Функцiя dms2rad перетворює значення кута, заданого в форматi “градуси–мiнути–секунди”, у радiани i має наступний формат виклику:

x := dms2rad(градуси, мiнути, секунди)

4

Наприклад, в результатi обчислення виразу

x := dms2rad(60, 20, 30.2345)

змiннiй x буде присвоєно значення 1.05316189636233, тобто виражене в радiанах значення кута 60◦ 20′ 30,2345′′.

Функцiя rad2dms перетворює значення кута, задане в радiанах, у формат “градуси–мiнути–секунди”; функцiя повертає вектор-рядок з трьох чисел. Рекомендується застосовувати цю функцiю тiльки для виведення результатiв. Приклад використання:

x := 1.05316189636233 rad2dms(x) = (60 20 30.2345)

1.4.Геоцентричнi декартовi, сферичнi та геодезичнi елiпсоїдальнi координати

Система координат, початок якої знаходиться в центрi мас Землi або близько нього, називається геоцентричною чи квазiгеоцентричною вiдповiдно. Тому координати, зв’язанi з загальноземним елiпсоїдом, називаються загальноземними i геоцентричними, а координати, зв’язанi з вибраним

референц-елiпсоїдом, — референцними i квазiгеоцентричними.

R

X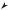

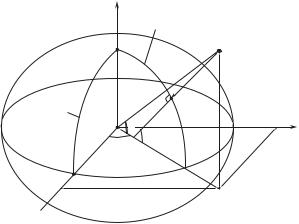
Рис. 1.4. Зображено вiсi системи геоцентричних декартових координат, довгота L, геоцентрична широта ϕ, геодезична широта B.

Декартовi координати X,Y , Z вводять таким чином, щоб початок координат O збiгався з центром вибраного елiпсоїда (загальноземного або референц-елiпсоїда), вiсь Z була направлена вздовж вiсi симетрiї елiпсоїда, а вiсi X та Y лежали в екваторiальнiй площинi елiпсоїда. Меридiан,

5

який проходить через точку перетину вiсi X та екватору елiпсоїда (точка R на рис. 1.4), приймається за початковий.

Положення точки Q в просторi можуть задавати також сферичнi координати: довгота L — це двогранний кут мiж площиною початкового меридiану та площиною меридiану точки Q (лежить в межах −180◦ < L 6 +180◦ або 0◦ 6 L < 360◦), геоцентрична широта ϕ — кут мiж радiус-вектором точки Q та екваторiальною площиною елiпсоїда (−90◦ 6 ϕ 6 +90◦), а також вiдстань r точки Q вiд початку координат (на рис. 1.4 це довжина вiдрiзка

OQ).

Зв’язок мiж координатами X,Y , Z та r, L, ϕ виражається формулами

X = r cos L cos ϕ

Z = r sin ϕ

Обернений перехiд вiд X,Y , Z до r, L, ϕ в лiтературi традицiйно записується в формi

arctg, а функцiєю atan2, яка є в рiзних математичних пакетах. Вона повертає виражене в радiанах значення кута мiж вiссю x i напрямком на точку площини з координатами (x, y). Цей кут вiдраховується вiд вiсi x проти годинникової стрiлки, а його значення лежить в межах вiд −π до +π.

На рис. 1.5 зображено кут α, який визначає напрямок на точку A з координатами (x, y). Очевидно, значення кута α не змiниться, якщо кожну з координат точки A домножити на додатне число k — отримаємо точку B з координатами (kx, ky), а якщо домножити на вiд’ємне число (−k), то

6

y

B

k y

A

y

- k y C

Рис. 1.5

отримаємо точку C з координатами (−kx, −ky), напрям на яку аж нiяк не буде α. Зi сказаного випливає, що обидва аргументи функцiї atan2 можна множити та дiлити на додатний множник, тобто atan2 (x, y), atan2 (kx, ky) та atan2 (x/k, y/k) повертають однаковий результат, якщо k > 0.

Нехай для кута α вiдомi значення sin α та cos α. Очевидно, що координати точки A будуть

p x = r cos α, y = r sin α, де r = x2 +y2, а значить,

α = atan2 (x, y) = atan2 (r cos α, r sin α) = atan2 (cos α, sin α)

Таким чином, функцiя atan2 дозволяє знаходити кут за вiдомими значеннями його синуса та косинуса.

З врахуванням сказаного, при практичних обчисленнях r, L, ϕ з формул

(1.7) потрiбно знаходити як

p p

r = X2 +Y 2 +Z2, L = atan2 (X, Y ) , ϕ = atan2 X2 +Y 2, Z . (1.8)

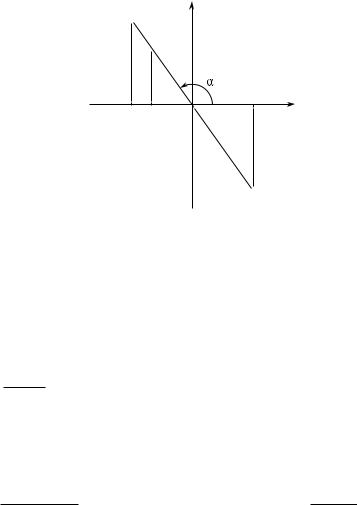
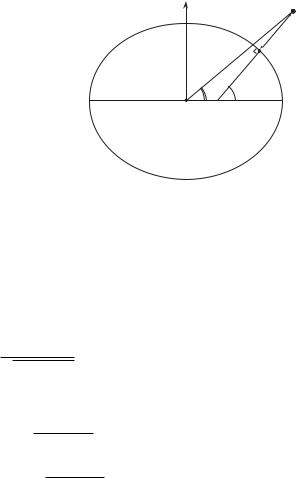
В геодезичних елiпсоїдальних координатах замiсть геоцентричної широти ϕ використовується геодезична широта B — це кут мiж проведеною з точки Q нормаллю (перпендикуляром) до поверхнi елiпсоїда та екваторiальною площиною (−90◦ 6 B 6 +90◦). На рис. 1.6 показано вiдмiннiсть мiж геоцентричною та геодезичною широтами. Висота H — це вiдстань мiж точкою Q та поверхнею елiпсоїда вздовж нормалi (на рис. 1.4 висота H дорiвнює довжинi вiдрiзка SQ). Нарештi, довгота L має той самий змiст, що i в системi сферичних координат.

7

Рис. 1.6. Геоцентрична широта ϕ та геодезична широта B

Формули переходу вiд декартових координат X,Y , Z до геодезичних координат B, L, H вiдносно земного елiпсоїда з параметрами a, e мають такий вигляд:

(1.9)

де N = p a

1−e2 sin2 B

Для зворотного переходу вiд X,Y , Z до B, L, H iснують такi формули:

В формулах (1.11), (1.12) значення tg B знаходиться послiдовними наближеннями: потрiбно спочатку з (1.11) знайти перше наближення tg B1, пiдставити його в праву частину (1.12), отримати наступне наближення tg B2, знову пiдставити його в праву частину (1.12) i т.д., аж поки не буде досягнута необхiдна точнiсть. Процес сходиться за 4–5 iтерацiй. Пiсля цього кут B можна обчислити як B = arctg(tg B).

Формула (1.13) непридатна при sin B ≈ 0. Тому наведемо iншi iтерацiйнi формули, якi придатнi для довiльних значеннях кута B та мають швидшу

8

Iснують також формули Боурiнга, якi дозволяють перейти вiд коорди-

тових секунд), а абсолютна похибка обчислення висоти H не перевищує 3·10−19 м, якщо вважати параметри a, b, e елiпсоїда WGS–84 точними.

Взаємнi перетворення геодезичних елiпсоїдальних та декартових геоцентричних координат виконують двi наступнi функцiї.

Функцiя BLH2XYZ, описана в файлi GeodeticLib.xmcdz, перетворює геодезичнi елiпсоїдальнi координати в декартовi геоцентричнi. Вона повертає вектор-стовпець з трьох чисел, а тому рекомендується виконувати присво-

єння трьом змiнним X, Y, Z у виглядi

X

Y := BLH2XYZ(B, L, H, a, e) Z

де a, e — екваторiальний радiус та ексцентриситет сфероїда; кути B, L задаються в радiанах, висота H — в метрах, якщо a задано в метрах. Приклад використання — в пунктi 1.8.

Функцiя XYZ2BLH перетворює декартовi геоцентричнi координати в

9

геодезичнi елiпсоїдальнi:

B

L := XYZ2BLH(X, Y, Z, a, e) H

(кути B, L повертаються в радiанах, висота H — в метрах, якщо a задано в метрах).

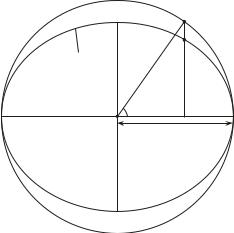
Система координат з приведеною широтою застосовується для задання положення точок, якi лежать безпосередньо на поверхнi елiпсоїда. Для цього потрiбнi лише двi координати — довгота L та приведена широта u, яка вводиться наступним чином. На великiй осi меридiанного елiпса як на дiаметрi побудуємо коло радiусом a (рис. 1.7). З точки Q проведемо перпендикуляр до екваторiальної площини елiпсоїда; точку перетину цього перпендикуляра з побудованим колом позначимо через Q′. Приведена широта точки Q — це кут мiж екваторiальною площиною та вiдрiзком OQ′ на рис. 1.7.

Q'

Q

меридіанний

еліпс

Рис. 1.7. До поняття приведеної широти

Декартовi геоцентричнi координати через приведену широту та довготу

10