
Вища геодезія
.pdf
Коефiцiєнти Ak, Bk в цих рядах є функцiями x.
|
A2 = − |
1 + ηx2 |
tg Bx, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
2 Nx2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
A = |
|
|
A2 |
|
(5 + 3 tg2 B + η2 |
|
9η2 tg2 |
B 4η4) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
x |
|
|
|
|
|
x |
|
|
|
x |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
− |
12 Nx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A6 = |
|
|
|
|
|
|
|
61 + (90 |
|
|
|
|
252ηx) tg Bx + 46ηx + 45 tg |
Bx(1 |
|
|
2ηx) |
, |
||||||||||||||||||||||||||||||||||||
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
360 Nx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A8 = |
|
|
− |
|
|
6 |
|
(1385 + 3633 tg Bx + 4095 tg |
Bx + 1575 tg Bx), |
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20160 Nx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(7.17) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B = |
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N cos Bx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
B = |
|
x |
B1 |
|
(1 + 2 tg2 B + η2), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
− |
6 Nx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B5 = |
|
|
|
|
(5 + 28 tg Bx + 24 tg Bx + 6ηx + 8ηx tg Bx), |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
120 N |
4 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
B7 = |
|
|
|
|
|
|
|
|
(61 + 662 tg |
|
Bx + 1320 tg |
|
|
Bx |
+ 720 tg |
|
Bx). |
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
5040 Nx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
e cos Bx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
позначено η |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
де |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
x |
|
|
|
|
√1 |
− |
e2 |
|
|
|
|
|
x |
|
|
p |
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 −e |
sin |
Bx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Продиференцiюємо ряди (7.13) по l: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
∂x |
|
= 2a2l + 4a4l3 + 6a6l5 + 8a8l7 + ..., |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
∂l |
|
|
|
|
|
|
(7.18) |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= b1 + 3b3l |
|
+ 5b5l |
|
+ 7b7l |
|
+ ..., |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
∂l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
Якщо коефiцiєнти |
a |
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
k, |
k обчисленi, то зближення меридiанiв та масштаб в |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
будь-якiй точцi можна знайти за формулами (7.8) та (7.9). |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
∂x |
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
s |
∂x |
2 |
|
|
∂y |
|
2 |
|
|
|
||||||||||||||
|
|
|
|
tg γ = |
|
. |
|
|
|
, |
|
|
m |
= |
|
|
|
+ |
|
. |
|
(7.19) |
|||||||||||||||||||||||||||||||||
|
|
|
|
∂l |
|
∂l |
|
|
N cos B |
∂l |
∂l |
|
|||||||||||||||||||||||||||||||||||||||||||
В MATLAB-програмi перехiд вiд геодезичних координат B, L до плоских декартових координат Гауса–Крюгера i навпаки здiйснюється за допомогою функцiй GK_BL2xy та GK_xy2BL.
GK_xy2BL на основi плоских координат Гауса–Крюгера x, y для елiпсоїда iз екваторiальним радiусом a та ексцентриситетом e повертає значення геодезичної широти B та рiзницi довгот dL (вона вiдповiдає величинi l, яка використовувалась у наведених вище формулах); формат виклику наступний:
[B, dL] = GK_xy2BL(x, y, a, e)
GK_BL2xy на основi геодезичної широти B та рiзницi довгот dL повертає для заданої точки значення плоских координат Гауса–Крюгера x, y, а також
значення зближення меридiанiв Gamma та масштабу m.
[x, y, Gamma, m] = GK_BL2xy(B, dL, a, e)
7.3.Редукування геодезичної лiнiї при переходi до координат Гауса–Крюгера
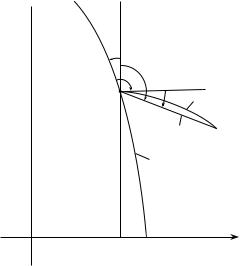
На рис. 7.4 показано зображення двох точок Q1 та Q2 в проекцiї Гауса– Крюгера. Криволiнiйний вiдрiзок, який їх сполучає — це зображення вiдрiзку геодезичної на елiпсоїдi. Кут A — це азимут геодезичної в точцi Q1; при конформному вiдображеннi вiн зберiгає своє значення.
Нехай (x1, y1) та (x1, y1) — це прямокутнi координати точок Q1, Q2; α — це кут мiж лiнiєю y = const та вiдрiзком Q1Q2.
Виявляється, що розв’язання оберненої геодезичної задачi на малi вiдстанi на поверхнi елiпсоїда можна наближено замiнити розв’язанням прямої та оберненої геодезичної задачi в прямокутних координатах xy, якщо точки Q1 та Q2 лежать в межах однiєї шестиградусної зони, причому азимут A та довжина s зображення вiдрiзку геодезичної лiнiї Q1, Q2 обчислюються за формулами:
s = d · 1 + 2Rm2 |
A= α+ γ −δ, |
+ 720Rm6 |
|
|||||
+ 24Rm2 + 24Rm4 |
||||||||
|
y2 |
|
y2 y4 |
|
y6 |
−1 |
||
|
m |
|
|
|
m |
|
m |
|
x 
γ
A α
Q1 |
δ s |
d  Q2
Q2
L = const
y
Рис. 7.4

де позначено |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
y + y |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
ym = |
1 |
|
2 |
, |
|
|
|
|
y = y2 −y1, |
|
|
x = x2 −x1, |
|||||||||
2 |
|
|
|
|
|||||||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
y |
|
y3 |
e2 sin Bm |
|
|||||
δ = |
|
|
|
|
|
|
ym |
|
|
|
|
|
|
m |
|
|
|
|
y2 y, |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
−2Rm2 |
|
|
|
− 6 − 3Rm2 − |
2 Rm3 |
m |
||||||||||||||
|
|
|
|
||||||||||||||||||
α = atan2 ( y, |
|
|
x) , |
|
|
|
|
|
|
|
|||||||||||
d = q |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
x2 + |
y2, |
|
|
|
|
|
|
|
|||||||||||||
Bm |
= |
|
B1 + B2 |
|
(B1, B2 — геодезичнi широти точок Q1, Q2), |
||||||||||||||||
2 |
√ |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||
Rm |
= |
|
|
a 1 −e |
|
|
|
— середнiй радiус кривизни на широтi Bm, |
|||||||||||||
|
(1 −e2 sin2 Bm)2 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
γ — зближення меридiанiв в точцi Q1.

Додаток А. Параметри загальноземних елiпсоїдiв, якi використовуються в деяких координатних системах
Таблиця 1.1
a — екваторiальний радiус елiпсоїда, м b — мала пiввiсь елiпсоїда, м
α— стиснення елiпсоїда
e— ексцентриситет елiпсоїда
e′ |
— другий ексцентриситет елiпсоїда |
GM |
— добуток гравiтацiйної сталої на масу Землi, м3/с2 |
J2, J4, J6 |
— коефiцiєнти зональних гармонiк |
ω— кутова швидкiсть обертання Землi, рад/с
U0 — нормальний потенцiал на поверхнi елiпсоїда, м2/с2 W0 — потенцiал на геоїдi, м2/с2
gекв — прискорення вiльного падiння на екваторi, м/с2 gпол — прискорення вiльного падiння на полюсi, м/с2
M— маса Землi, кг
GRS-80
Визначаючi параметри:
a |
= 6 378 137 |
GM = 3,986 005 |
·1014 |
|
J2 |
= 1,082 63 ·10−3 |
ω |
= 7,292 115 |
·10−5 |
|
Похiднi параметри: |
|
||
b |
= 6 356 752,314 140 |
J4 |
= −2,370 912 22 ·10−6 |
|
α |
= 1/298,257 222 101 |
J6 |
= 6,083 47 ·10−9 |
|
e2 |
= 0,006 694 380 022 901 |
J8 |
= −1,427 ·10−11 |
|
e′2 |
= 0,006 739 496 775 48 |
gекв = 9,780 326 771 5 |
||
U0 |
= 62 636 860,850 |
gпол = 9,832 186 368 5 |
||
|
|
WGS-84 |
|
|
|
|
|
||
|
Визначаючi параметри: |
|
||
a |
= 6 378 137 |
GM = 3,986 004 418 ·1014 ±8 ·105 |
||
α |
= 1/298,257 223 563 |
ω |
= 7,292 115 |
·10−5 |
|
Похiднi параметри: |
|
||
b |
= 6 356 752,314 245 |
J2 |
= 1,082 629 821 313 3 ·10−3 |
|
e |
= 0,081 819 190 842 622 |
U0 |
= 62 636 851,714 6 |
|
e2 |
= 0,006 694 379 990 14 |
gекв = 9,780 325 335 9 |
||
e′ |
= 0,082 094 437 949 696 |
gпол = 9,832 184 937 8 |
||
e′2 |
= 0,006 739 496 742 28 |
M |
= 5,973 332 8 ·1024 |
|
|
|
ПЗ-90 |
|
|
|
|
|
||
a |
= 6 378 136 |
GM = 3,986 004 4 ·10− |
||
|
|
|
|
14 |
α |
= 1/298,257 839 303 |
J2 |
= 1,082 625 7 ·10 3 |
|

e2 |
= 0,006 694 366 193 10 |
U0 |
= 62 636 861,074 |
ω |
= 7,292 115 ·10−5 |
|
|
|
IERS-96 |
||
|
|
|
|
a |
= 6 378 136,49 |
GM = 3,986 004 418 ·1014 |
|
α |
= 1/298,256 45 |
J2 |
= 1,082 635 9 ·10−3 |
e2 |
= 0,006 694 397 236 |
U0 |
= 62 636 856,85 |
ω |
= 7,292 115 ·10−5 |
|
|
|
IERS-2002 |
||
|
|
|
|
a |
= 6 378 136,6 ±0.1 |
GM = 3,986 004 418 ·1014 ±8 ·105 |
|
α |
= 1/298,256 42 ±0,000 01 |
J2 |
= 1,082 635 9 ·10−3 ±10−10 |
ω |
= 7,292 115 ·10−5 |
W0 |
= 62 636 856,0 ±0,5 |
|
|
gекв = 9,780 327 8 ±10−6 |
|
IERS Conventions (2003) рекомендує значення G = (6,673 ±0,010) ·10−11
IAG рекомендує значення G = (6,67259 ±0,0003) ·10−11 |
м3 |
|
|
. |
|
кг· с2 |
||
CODATA в 2002 р. рекомендувала значення G = (6,6742 ±0,0010) ·10−11
м3 кг· с2 .
м3
кг· с2

Додаток Б. Особливостi виконання символьних обчислень
в MATLAB
Б.1. Поєднання символьних та числових обчислень
В п. 3.5 та 3.8 для дослiдження просторової кривої використовуються засоби символьної математики MATLAB.
Нагадаємо, що для роботи з символьною математикою в MATLAB повинен бути встановлений Symbolic Math Toolbox. Традицiйно робота з символьною математикою включає в себе оголошення в програмi символьних змiнних, створення символьних (аналiтичних) виразiв та їх перетворення за допомогою вiдповiдних функцiй, а також пiдстановку в символьнi вирази числових значень i отримання результатiв в числовому виглядi.
Символьнi змiннi в програмi створюються або за допомогою функцiї syms, або шляхом присвоєння змiннiй символьного виразу, наприклад:
% оголошуємо символьнi змiннi a, b, t
syms a b t
% створюємо символьну змiнну f, якiй присвоєно значення − символьний вираз f = a*cos(2*t) + b*sin(3*t);
Одна з функцiй Symbolic Math Toolbox, яка використовувалась в п. 3.5 та 3.8 — це функцiя diff, призначена для обчислення похiдних. Її аргументи
— це вираз, вiд якого треба взяти похiдну, та змiнна, по якiй береться похiдна. Наприклад,
% обчислюємо першу похiдну вiд f по t df = diff(f, t);
%в результатi df = 3*b*cos(3*t) - 2*a*sin(2*t)
%обчислюємо другу похiдну вiд f по t
d2f = diff(f, t, 2);
% в результатi d2f = - 9*b*sin(3*t) - 4*a*cos(2*t)
Диференцiювати можна i символьний вектор, наприклад,
r= [t^2; 3*t; exp(a*t)];
dr = diff(r, t);
% в результатi dr = [2*t; 3; a*exp(a*t)]
Для пiдстановки в символьнi вирази iнших виразiв та числових значень використовується функцiя subs (вiд англ. substitute), яка в програмi найчастiше викликається в такому форматi:
NewExpr = subs(Expr, змiнна, значення)
де Expr — символьний вираз або змiнна, якiй присвоєно символьний вираз; в цей вираз буде здiйснюватись пiдстановка;

змiнна — iм’я змiнної, замiсть якої буде пiдставлено значення, яке в свою чергу може бути iншим символьним виразом або числом.
Якщо потрiбно зробити одночасно декiлька пiдстановок, формат виклику функцiї subs має бути таким:
NewExpr = subs(Expr, {змiнна1, змiнна2, ...}, {значення1, значення2, ...})
syms a b x y t
%вираз, в який буде зроблена пiдстановка f = a*cos(2*t) + b*sin(3*t);
%замiсть змiнних a i b пiдставляємо вiдповiдно вирази x^2 i y^3
f1 = subs(f, {a, b}, {x^2, y^3});
%в результатi f1 = cos(2*t)*x^2 + sin(3*t)*y^3
%замiсть змiнних a, b, t пiдставляємо вiдповiдно числа 4, 5, 1
f2 = subs(f, {a, b, t}, {4, 5, 1}); % в результатi f2 = 4*cos(2) + 5*sin(3)
Продемонстрована пiдстановка не впливає на змiннi a, b, t.
Ще один варiант пiдстановки полягає в тому, щоб в програмi виконати присвоєння числових значень або символьних виразiв необхiдним змiнним, а потiм викликати функцiю subs лише з одним аргументом:
a = 4; b = 5; t = 1;
f2 = subs(f);
% в результатi f2 = 4*cos(2) + 5*sin(3)
Зауважимо, що при цьому змiннi a, b, t в результатi присвоєння набувають типу double. Якщо ж необхiдно, щоб змiннi a, b, t залишались символьними, присвоєння слiд виконувати так:
a = sym(4); |
b = sym(5); |
t = sym(1); |
f2 = subs(f);
В наведених вище прикладах змiнна f2 мiстить символьний вираз, який вже “готовий” до перетворення в число з плаваючою комою. Отримати результат в числовому виглядi можна декiлькома способами:
% 1) перетворення засобами арифметики довiльної точностi; кiлькiсть цифр контролюється функцiєю digits
f3 = vpa(f2);
%в результатi f3 = -0.9589873058892334374865489039625,
%але f3 − це символьна змiнна
%2) перетворення засобами арифметики довiльної точностi; кiлькiсть цифр задається явно

f4 = vpa(f2, 6);
%в результатi f4 = -0.958987, але f4 − це теж символьна змiнна
%3) перетворення в тип double (число з плаваючою комою подвiйної точностi)
f5 = double(f2);
% в результатi f5 = -0.958987305889233, але f5 − це змiнна типу double
Б.2. Символьнi операцiї з векторами
Такi часто уживанi операцiї з векторами, як скалярний i векторний добуток та знаходження модуля вектора, в MATLAB виконують функцiї dot, cross та norm вiдповiдно. Вони розрахованi на роботу з векторами числового типу; при спробi застосувати їх до символьних векторiв результат не завжди задовольняє користувача. Розглянемо приклад.
clc, clear all
syms ax ay az bx by bz
% створюємо два символьних вектора−стовпця a = [ax; ay; az];
b = [bx; by; bz];
D = dot(a, b);
% в результатi D = bx*conj(ax) + by*conj(ay) + bz*conj(az)
C = cross(a, b);
% в результатi C = [ ay*bz-az*by; az*bx-ax*bz; ax*by-ay*bx ]
N = norm(a);
% в результатi N = (abs(ax)^2 + abs(ay)^2 + abs(az)^2)^(1/2)
Бачимо, що iз знаходженням векторного добутку проблем не виникає, але при знаходженнi скалярного добутку та модуля вектора результат мiстить функцiю conj, яка означає комплексне спряження (комплексно спряженим до числа z = x + yi називається число z = x − yi), та функцiю abs, яка означає знаходження абсолютної величини (модуля) числа, тобто ска-
лярний добуток векторiв та модуль вектора обчислюються за правилами q
|
#„ |
= axbx + ayby + azbz, |
| a | = |ax|2 |
+ |ay|2 + |az|2. |
a · b |
||||
#„ |
|
|
#„ |
|
Справа в тому, що вбудована в MATLAB система символьної математики всi символьнi змiннi по замовчуванню вважає комплексними. Щоб позбутися функцiй conj та abs в символьних результатах, потрiбно при оголошеннi символьних змiнних поставивши в кiнцi списку змiнних ключове слово real, указавши тим самим, що вони є дiйсними величинами.

clc, clear all
syms ax ay az bx by bz real
a = [ax; ay; az]; b = [bx; by; bz];
D = dot(a, b);
% в результатi D = ax*bx + ay*by + az*bz
% три способи обчислення модуля вектора:
N = simplify(norm(a));
N= sqrt(a' *a);
N= sqrt(dot(a, a));
% всi вони дають в результатi N = (ax^2 + ay^2 + az^2)^(1/2)
Б.3. Виведення результатiв символьних обчислень
Переглядати результати символьних обчислень, звичайно, можна шляхом виведення до командного вiкна значень символьних змiн та виразiв, але цей спосiб не завжди зручний i вже зовсiм не придатний для перегляду громiздких результатiв. Бiльш ефективний варiант — скористатися функцiєю ShowSym, яка входить до складу бiблiотеки GeodeticLib; її створив автор тiєї ахiнеї, яку ви зараз читаєте.
Функцiя ShowSym видає значення символьного виразу у виглядi повноцiнної формули в спецiальне вiкно Web Browser. Наступна коротка програма демонструє роботу функцiї.
|
clc, clear |
|
|
|
ClearSymOutput |
|
|
|
syms x y |
|
|
|
f = x^2 + y^2 |
|
|
|
ShowSym(x, |
sin(x)*cos(y), f, ' f=f ' ) |
|
|
ShowSym( ' \sqrt{\alpha} = f^3 + f^5 ' , ' текстовий коментар ' , ' F ' ) |
|
|
|
x = 10; |
y = 20; |
|
|
ShowSym( ' f |
= f = subs(f) ' ) |
|
|
|
|
|
В результатi роботи програми вiдкривається вiкно Web Browser з наступним змiстом — див. рис. Б-1.
Робота функцiї ShowSym заснована на перетвореннi значень символьних виразiв у формат LATEX. Перетворенi рядки дописуються в файл ShowSymOutput.m, який створюється в поточнiй папцi. Потiм засобами MATLAB змiст цього файлу “публiкується” у виглядi файлу ShowSymOutput.html, який розташовується в папцi html\ поточної папки.

x
sin(x)*cos(y)
f
'f'
'\sqrt{\alpha}=f^3+f^5'
'текстовий коментар' 
'F'
'f = f = subs(f)'
Рис. Б-1. Вiдповiднiсть мiж аргументами функцiї ShowSym та виданими результатами у вiкнi Web Browser
Нарештi, файл ShowSymOutput.html вiдкривається за допомогою вбудованого в MATLAB веб-навiгатора Web Browser. Функцiя ShowSym може викликатись декiлька разiв в програмi; при кожному виклику дописуються новi рядки в iснуючий файл ShowSymOutput.m, який при цьому “публiкується” заново. Тому на початку програми рекомендується викликати функцiю ClearSymOutput, яка закриває вiкно Web Browser, видаляє з поточної папки файл ShowSymOutput.m та папку html\ разом з її змiстом. В програмi цю функцiю слiд викликати до першого виклику функцiї ShowSym.
Функцiя ShowSym приймає довiльну кiлькiсть аргументiв; окремий аргумент може бути символьним виразом, або символьним рядком (тобто заключеним в одинарнi лапки). Для кожного аргумента у вiкно Web Browser окремим рядком видається свiй результат.
Якщо черговий аргумент функцiї ShowSym є символьним виразом, то у вiкно Web Browser видається просто значення цього виразу. Так, наприклад, символьним змiнним x та y нiчого не присвоєно, а тому для
