20. Параллельность плоскостей

Если у двух плоскостей линия пересечения несобственная прямая, т.е. она бесконечно удалена, то плоскости параллельны.

На комплексном чертеже две пересекающиеся прямые одной плоскости должны быть соответственно параллельны двум пересекающимся прямым другой плоскости.

Ω (c∥d), 12⊂Ω, l∋M, l∥c; h∋M, h∥12⇒Σ(l⋂h)∥Ω

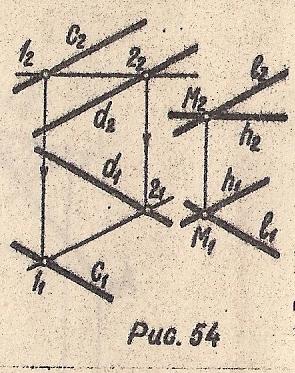
Рис. 54

21. Параллельность прямой и плоскости

Прямая, параллельная плоскости, если она параллельна какой-либо прямой, принадлежащей этой плоскости. На Рис. 55 через точку К проведена прямая l, параллельная плоскости Σ(a⋂b). Проводим в плоскости Σ произвольную прямую 12. 12⊂Σ, l∋K l∥12⇒l∥Σ

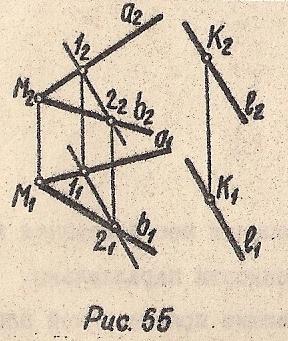
Рис. 55

22. Перпендикулярность прямой и плоскости

Из стереометрии известно, что прямая n перпендикулярна плоскости, если она перпендикулярна любым двум пересекающимся прямым этой плоскости (Рис. 56).

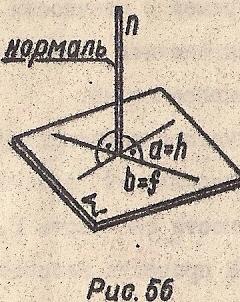
Рис. 56

Вместо произвольных пересекающихся прямых можно провести в плоскости h и f. Тогда прямая и плоскость общего положения будут взаимно перпендикулярны в том и только в том случае, если проекции прямой будут перпендикулярны одноименным проекциям соответствующих линий уровня, т.е. горизонтальная проекция прямой –перпендикулярна горизонтальной проекции горизонтали n₁⊥h1, а фронтальная проекция прямой-перпендикулярна фронтальной проекции фронтали n₂⊥f₂ (по теореме о проецировании прямого угла).

На Рис. 57 показано, как восстановить перпендикуляр к плоскости в точке А. Прямая n перпендикулярна к плоскости Σ (f⋂h), так как n₁⊥h1 и n₂⊥f₂ (Рис. 57 а).

Рис. 57

На эпюре (смотрите Рис. 57 б). Перпендикуляр к плоскости называют нормалью и обозначают «n». Используя условия перпендикулярности прямой и плоскости, можно при помощи нормали (перпендикуляра) определить напраление плоскости и строить плоскости заданных направлений.

На Рис. 58 показано, как из точки А опустить перпендикуляр на плоскость Σ(f⋂h). Определить направление нормали n плоскости Σ.

На Рис 59 – как через точку М провести плоскость Γ, зная направление нормали n.

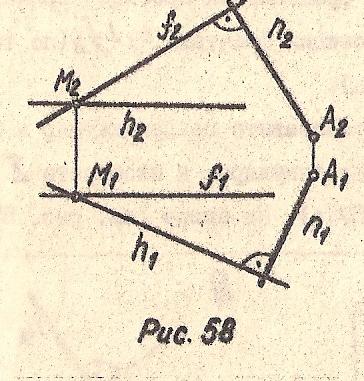
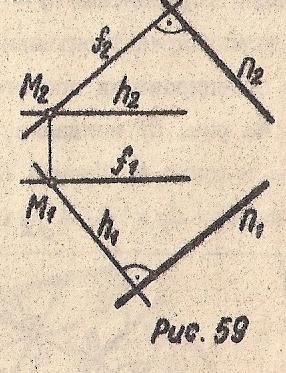
Рис. 58 Рис. 59

23. Перпендикулярность плоскостей

Как известно из стереометрии, если две плоскости взаимно перпендикулярны, то каждая их них проходит через перпендикуляр к другой плоскости.

Иначе, две плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой. Отсюда следует два способа построения взаимно перпендикулярных плоскостей Σ и Ω: либо плоскость Ω проводится через прямую n, перпендикулярно плоскости Σ; либо плоскость Σ проводится перпендикулярно прямой n, принадлежащей плоскости Ω.

Построение взаимно перпендикулярных плоскостей сводится к построению перпендикулярных прямой и плоскости (Рис.60)

1. Ω ⊃ n; n ⊥ Σ (f⋂h) ⇒ n₁⊥h₁ h₂⊥f₂

2. Σ ⊥ n (n₁⊥h₁ n₂⊥f₂)

3. Ω⊥Σ

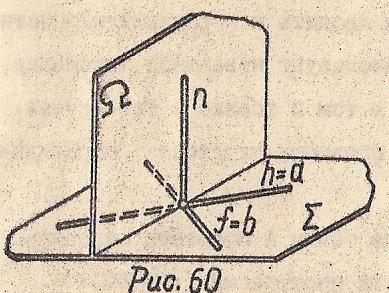
Рис. 60

На Рис. 61 показано, как через прямую l провести плоскость, перпендикулярную плоскости Σ (a∥b)

1. K∈l⇒(K₁∈l₁ K₂∈l₂

2. Σ (a∥b)⇔Σ(f⋂h)

3. (n₁ ⊥ h₁ n₂ ⊥ f₂)⇒n ⊥ Σ⇒Ω (n⋂l) ⊥ Σ(a∥b)

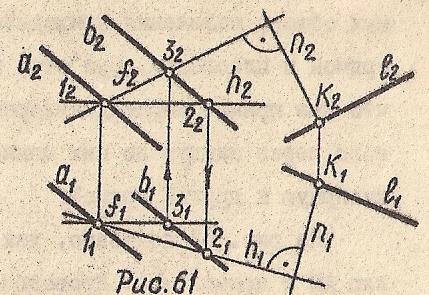
Рис. 61