14. Плоскости частного положения

Плоскости, перпендикулярные одной или двум плоскостям проекций называются проецирующими. Они характеризуются тем, что хотя бы одна из проекций плоскости будет вырождаться в прямую линию – след этой плоскости, а все геометрические элементы (фигуры), принадлежащие этой плоскости, будут проецироваться на след этой плоскости.

1. Проецирующие плоскости

Плоскость перпендикулярная горизонтальной плоскости проекций П₁, называется горизонтально-проецирующей плоскостью (Рис. 38)

Ω(l ⋂ n) ⊥ П₁; Ω ⋂ П₁=Ω₁- след плоскости, l₁=n₁=Ω₁; ∠β₁≌∠β

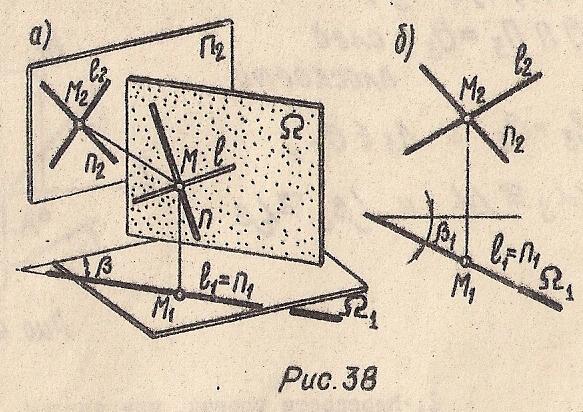
Рис. 38

Плоскость, перпендикулярная фронтальной плоскости проекций П₂, называется фронтально-проецирующей (Рис 39)

Σ(АВС) ⊥ П₂; Σ ⋂ П₂=Σ₂ - след плоскости, А₂В₂С₂=Σ₂; ∠α₂≌∠α

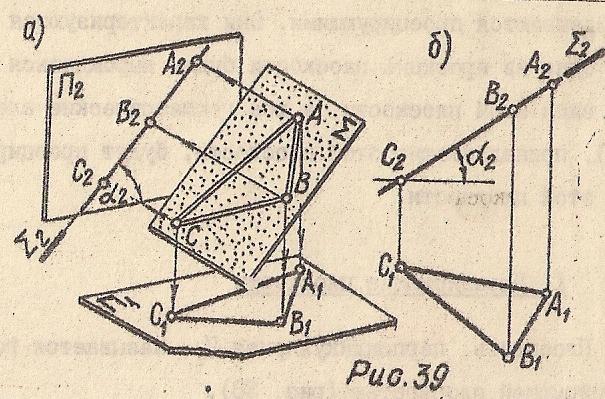
Рис. 39

Плоскость, перпендикулярная профильной плоскости проекций П₃, называется профильно-проецирующей плоскостью (Рис. 40)

Θ(l, A) ⊥ П₃; θ ⋂ П₃ = θ₃ - след плоскости, l=θ₃ и А₃ ∈θ₃; ∠α₃≌∠α, ∠β₃≌∠β

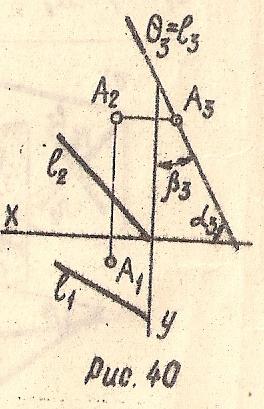
Рис. 40

2. Плоскости уровня, или дважды проецирующие плоскости

Плоскость параллельная П₁, называется горизонтальной плоскостью (Рис41)

А₂В₂С₂=Σ∥Х, А₁В₁С₁≌АВС

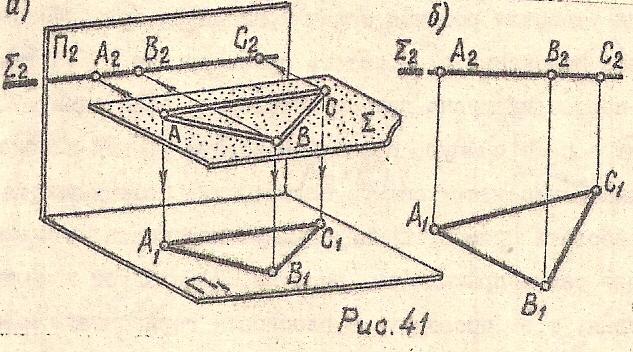
Рис. 41

Плоскость параллельная П₂ называется фронтальной плоскостью (Рис. 42)

Ω (l ⋂ m)∥П₂; Ω⋂П₁=Ω₁ – след плоскости, l₁=m₁=Ω₁∥X

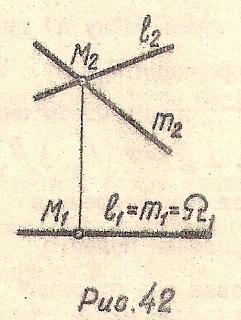
Рис. 42

Плоскость, параллельная П3, называется профильной плоскостью (Рис. 43)

θ (l, А)∥П₃; θ⋂П₁=θ₁ и θ ⋂ П₂ = θ₂– следы плоскости, l₁= θ₁ и l₂= θ₂; θ₁ и θ₂ ⊥ X

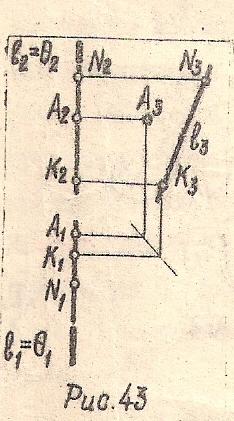
Рис. 43

15. Построение третьей проекции (Преобразование эпюра плоскости)

Иногда для удобства решения задач приходится преобразовывать плоскость общего положения в плоскость проецирующую. Известно, что плоскость перпендикулярна другой плоскости, если одна из плоскостей содержит в себе прямую, перпендикулярную другой плоскости.

При преобразовании плоскости общего положения в проецирующую, достаточно преобразовать прямую, принадлежащую этой плоскости, в проецирующую. В качестве таких прямых (смотрите Рис. 22, Рис. 23) следует использовать линии уровня, т.е. проводить в плоскости горизонталь или фронталь.

На Рис. 44 показано преобразование плоскости общего положения Σ(АВС) в проецирующую в системе П₄⊥П₁. Проводим в плоскости (можно через точку А) горизонталь h(h₂∥X₁₂). Водим плоскость проекций П₄⊥П_1. Чтобы плоскость П₄ была бы перпендикулярна Σ, надо чтобы она была перпендикулярна горизонтали h. На основании теоремы о проецировании прямого угла новая ось проекций Х'₁₄ ⊥h₁. Затем находим новые проекции точек на плоскости П₄: А₄В₄С₄ (смотрите Рис.14), для чего откладываем отрезки А₄А_Х'=А₂А_Х, В₄В_Х'=В₂В_Х и т.д. След (третья проекция) Σ₄ проходит через точки А₄ и В₄

П₄⊥Σ⇒П₄⊥h, ∠α₄≌∠α

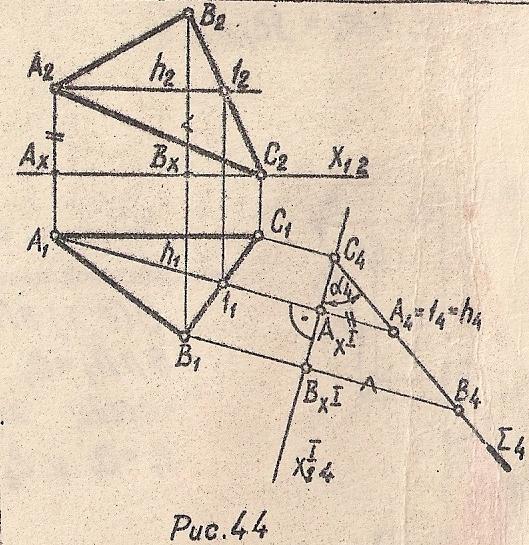
Рис. 44

16 Позиционные задачи

В позиционных задачах рассматривается только положение геометрических образов (фигур) относительно плоскостей проекций и относительно друг друга, без учета их метрической сущности, т.е. без их измерений.

Все позиционные задачи могут быть разбиты на три группы:

1. Задачи на взаимное расположение геометрических образов (прямая и плоскости общего и частного положения).

2. Задачи на принадлежность одного геометрического образа другому (принадлежность точки и прямой; прямой и плоскости, точки и плоскости).

3. Задачи на пересечение геометрических образов:

• задачи на пересечение двух линий;

• задачи на пересечение линии и плоскости;

• задачи на пересечение плоскостей.