9. Взаимопринадлежность точки и прямой

Если точка принадлежит прямой, то проекция точки располагается на одноименных проекциях прямой (смотрите Рис. 16).

K∈l⇒K₁∊l₁ и K₂∊l₂

10. Взаимное расположение двух прямых

В пространстве две прямые могут пересекаться или скрещиваться.

Две прямые могут пересекаться в том случае, если они лежат в одной плоскости. На эпюре их одноименные проекции должны пересекаться, а проекции точки их пересечения должны лежать на общей линии связи (Рис. 24).

a ⋂ b⇒(a₁ ⋂ b₁ и a₂ ⋂ b₂), K₁K₂⊥x

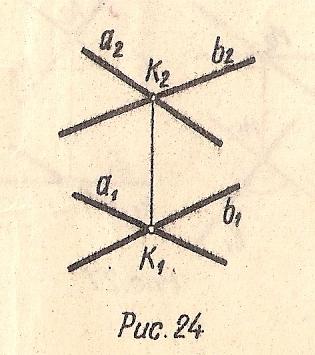
Рис. 24

Прямые линии пересекающиеся в несобственной точке, называются параллельными. На эпюре их одноименные проекции параллельны (Рис. 25)

c∥d⇒(c₁ ∥d₁ и c₂ ∥d₂)

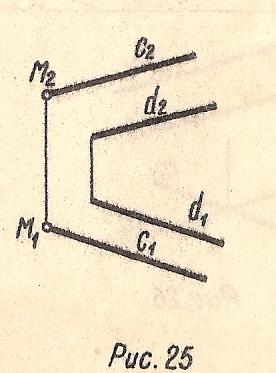
Рис. 25

Если прямые не принадлежат одной плоскости, т.е. не пересекаются и не параллельны, то они скрещиваются (Рис. 26)

m∸n

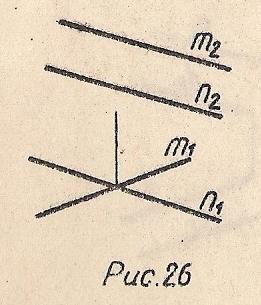
Рис.26

Частный случай пересекающихся прямых

Две взаимно перпендикулярные прямые спроецируются взаимно перпендикулярно на плоскость проекций, если одна из них параллельна плоскости проекций, а другая не будет ей перпендикулярна (Рис. 27). (Смотрите теорему, Рис. 7).

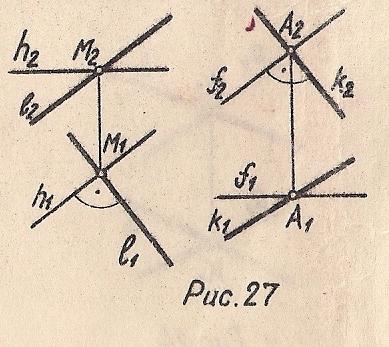
Рис. 27

IV. Плоскость

II. Задание плоскости на эпюре

Плоскость – это совокупность однородных или различных множеств. Плоскость считается заданной, если из всех точек пространства можно выделить только те точки, которые принадлежат данной плоскости.

Определителем плоскости называют совокупность условий, необходимых и достаточных для задания плоскости.

Определителями плоскости могут быть:

1. Три точки, не лежащие на одной прямой (Рис. 28 а); Σ(АВС)

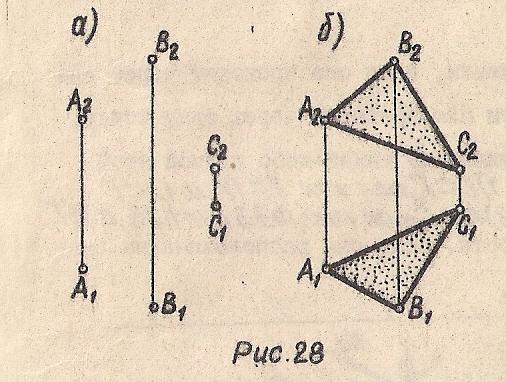
Рис. 28

2. Прямая и точка вне ее (Рис. 29); θ (l, A)

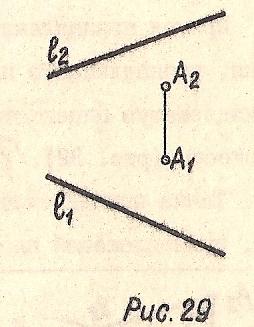
Рис. 29

3. Две параллельные прямые (Рис. 30); Ω (m∥n)

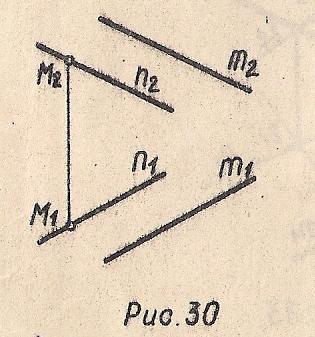
Рис. 30

4. Две пересекающиеся прямые (Рис. 31а) Γ(b⋂c)

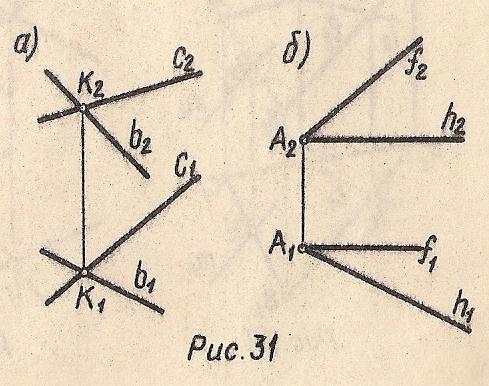
Рис. 31

Удобно задавать плоскость пересекающимися прямыми, но не общего положения, а частного. На Рис. 31 б плоскость задана пересекающимися горизонталью h и фронталью f.

12. Прямая и точка в плоскости

Прямая принадлежит плоскости, если она проходит через две точки, принадлежащие плоскости или проходит через одну точку, принадлежащую плоскости, параллельно какой-либо прямой этой плоскости (Рис. 32).

Γ(АВС): l⊂Γ, т.к. l⊂12, а 12⊂Γ; m⊂Γ, т.к. m∋3 и m∥AB, a 3∈Γ

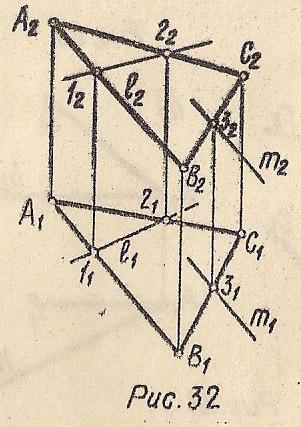
Рис. 32

Точка принадлежит плоскости, если она расположена на прямой, принадлежащей плоскости. На Рис. 33 показано построение фронтальной проекции точки А₂, принадлежащей плоскости Σ(m∥n), по заданной горизонтальной проекции А₁.

А∈Σ, т.к. А∈12, а 12⊂Σ

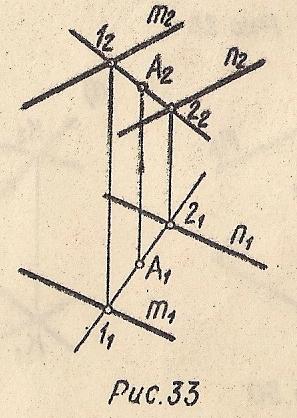
Рис. 33

13.Главные линии плоскости

Главные линии плоскости – это особые прямые, принадлежащие плоскости, позволяющие более точно выявить ориентацию плоскости отьносительно плоскостей проекций и упростить решение многих задач.

Главными линиями являются прямые уровня: горизонталь-h; фронталь - f; профильная – p; а также линии наибольшего наклона, при помощи которых можно определить угол наклона плоскости к плоскостям проекций П₁, П₂, П₃.

1. Горизонталь – это прямая, принадлежащая плоскости и параллельна плоскости проекций П₁ (Рис. 34)

h⊂Σ (l⋂b), т.к. h⊂12, а 12⊂Σ; h∥П1⇒h2∥X

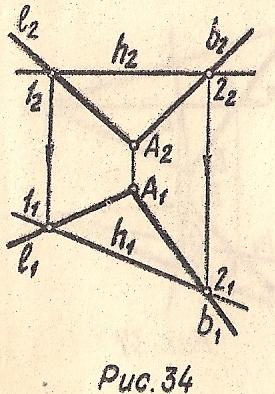
Рис. 34

2. Фронталь – это прямая, принадлежащая плоскости и параллельная плоскости проекций П2 (Рис. 35).

f⊂θ (m∥n), т.к. f⊂12, а 12⊂θ; f∥П₂⇒f₁∥X

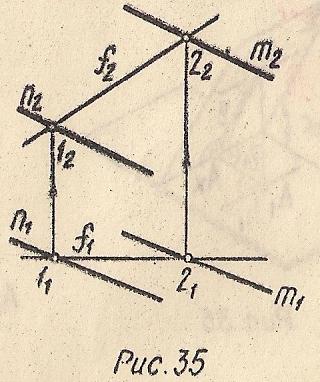
Рис. 35

3. Линия наибольшего наклона-это прямые, принадлежащие плоскости и перпендикулярны соответственно горизонталям, фронталям и профильным прямым (Рис. 36).

h⊂Σ и h∥П₁; l⊥h; =∠α, т.к. l⊂Σ, а ∠α

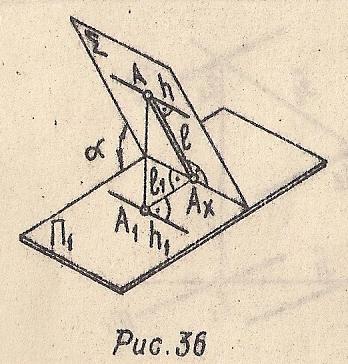
Рис. 36

На Рис. 37 показано; как провести в плоскости треугольника АВС через точку В линию наибольшего наклона к плоскости проекций П₁. Линия наибольшего наклона к плоскости П₁ называется еще линией ската (по направлению этой линии «скатываются» капли жидкости). На основании теоремы о проецировании прямого угла:

BD ⊥ h; h∥П₁⇒ B₁D₁ ⊥ h₁, BD ⊂Σ и h⊂Σ

Рис. 37