
- •Глава 1. Линейное программирование 3
- •Глава 2. Транспортная задача линейного программирования (тз) 68
- •Глава 3. Динамическое программирование 98
- •Глава 1. Линейное программирование
- •1.1. Математическая модель задачи линейного программирования
- •1.2. Формы записи задач линейного программирования
- •Рассмотрим приемы, позволяющие переходить от одной формы записи задачи к другой
- •1.3. Геометрическая интерпретация и графический метод решения задач линейного программирования с двумя переменными
- •Алгоритм графического метода решения злп с двумя переменными
- •1.4. Графический метод решения задач линейного программирования сnпеременными
- •1.5. Симплексный метод решения задач линейного программирования
- •Алгоритм решения злп симплексным методом
- •Нахождение начального опорного плана злп ( )
- •Нахождение начального опорного плана злп методом искусственного базиса
- •Нахождение начального опорного плана злп методом Жордановых исключений
- •Шаг Жордановых исключений осуществляется по следующим правилам:
- •Исследование на оптимальность опорного плана при решении злп на
- •Переход к новому опорному плану
- •1.6. Двойственные задачи линейного программирования
- •Правила построения двойственной задачи.
- •Глава 2. Транспортная задача линейного программирования (тз)
- •2.1. Математическая модель транспортной задачи
- •Закрытая и открытая модели транспортной задачи
- •2.2. Решение транспортной задачи
- •Алгоритм решения транспортной задачи
- •Нахождение начального опорного плана методом «минимального элемента»
- •Нахождение начального опорного плана методом «северо-западного угла»
- •Нахождение начального опорного плана методом Фогеля
- •Проверка на оптимальность невырожденного опорного плана методом потенциалов
- •Переход к новому опорному плану
- •Цикл пересчета
- •Глава 3. Динамическое программирование
- •3.1. Задача оптимального распределения ресурсов
- •I этап. Условная оптимизация.
- •II этап. Безусловная оптимизация.
- •3.2. Задача об оптимальной стратегии замены оборудования
- •I этап. Условная оптимизация.
- •II этап. Безусловная оптимизация.
- •Список использованной литературы
1.5. Симплексный метод решения задач линейного программирования
Симплексный метод основывается на следующем:
ОДР ЗЛП является выпуклым множеством с конечным числом угловых точек, т.е. многогранником или многоугольным множеством;
оптимальным решением ЗЛП является одна из угловых точек ОДР, если оптимальное решение единственно и не более двух угловых точек ОДР, если оптимальных решений бесконечное множество;
угловые точки ОДР алгебраически представляют некоторые опорные решения системы ограничений задачи (опорные планы).
Данный метод состоит в целенаправленном переборе опорных решений ЗЛП. Он позволяет за конечное число шагов расчета либо найти оптимальное решение, либо установить его отсутствие.
Алгоритм решения злп симплексным методом
Привести ЗЛП к каноническому виду с неотрицательной правой частью.
Найти какой-либо начальный опорный план
 .
Если опорный план отсутствует, то задача
не имеет решения вследствие несовместности
системы ограничений.
.
Если опорный план отсутствует, то задача
не имеет решения вследствие несовместности
системы ограничений.Проверить найденный план на оптимальность, используя оценки заполненной симплексной таблицы.
Если план оптимален, то задача решена.
Если план оптимален, но не единственен, то можно найти еще один оптимальный план.
Если план не оптимален, но имеет место условие неограниченности целевой функции, то задача не имеет решения.
Если пункты 4) – 6) алгоритма не выполняются, найти новый опорный план и перейти к пункту 3).
Нахождение начального опорного плана злп ( )
Пусть система ограничений ЗЛП представлена в канонической форме записи с неотрицательной правой частью.
![]()
![]()
![]() .
.
Говорят,
что ограничение ЗЛП имеет предпочтительный
вид,
если при неотрицательной правой части
(![]() )
левая часть ограничения содержит
переменную, входящую с коэффициентом,
равным единице, а в остальные
ограничения-равенства – с коэффициентом,
равным нулю.
)
левая часть ограничения содержит
переменную, входящую с коэффициентом,
равным единице, а в остальные
ограничения-равенства – с коэффициентом,
равным нулю.
Например, в системе ограничений:

первое и второе ограничения имеют предпочтительный вид, а третье – нет (предпочтительные переменные подчеркнуты).
Если каждое ограничение системы имеет предпочтительный вид, то система представлена в предпочтительном виде. В этом случае легко найти ее опорное решение. Предпочтительные переменные будут базисными, а остальные – свободными. Все свободные переменные нужно приравнять к нулю, тогда базисные переменные будут равны свободным членам.
Например, в системе ограничений:

предпочтительными
(базисными) являются переменные
![]() ,
свободными являются переменные
,
свободными являются переменные![]() .
.
Приравниваем
свободные переменные
![]() к нулю, тогда базисные переменные примут
значения:
к нулю, тогда базисные переменные примут
значения:![]() ,
,![]() ,
,![]() .
.
Получим
начальный опорный план
![]() .
.
В случае, когда в каноническом виде с неотрицательной правой частью система ограничений ЗЛП не имеет предпочтительного вида, то начальный опорный план можно найти методом искусственного базиса или методом Жордановых исключений.
Нахождение начального опорного плана злп методом искусственного базиса
В
случае, когда ограничение-равенство
системы не имеет предпочтительного
вида, к его левой части добавляют
искусственную переменную
![]()
![]() .
В целевую функцию переменные
.
В целевую функцию переменные![]()
![]() вводят с коэффициентом «M»
в случае решения задачи на минимум и с
коэффициентом «–М» в случае решения
задачи на максимум, где М – большое (по
сравнению с остальными коэффициентами
целевой функции) положительное число.
Полученная задача называется М-задачей,
соответствующей исходной. Она всегда
имеет предпочтительный вид.
вводят с коэффициентом «M»
в случае решения задачи на минимум и с
коэффициентом «–М» в случае решения
задачи на максимум, где М – большое (по
сравнению с остальными коэффициентами
целевой функции) положительное число.
Полученная задача называется М-задачей,
соответствующей исходной. Она всегда
имеет предпочтительный вид.
Пусть ЗЛП имеет каноническую форму записи с неотрицательной правой частью:

где
![]()
![]() .
.
Если ни одно из ограничений не имеет предпочтительной переменной, то М-задача запишется так:

Тогда
начальный опорный план этой задачи:
![]()
Если некоторое уравнение системы имеет предпочтительный вид, то в него не следует вводить искусственную переменную.
Пример 1.13
Найти начальный опорный план ЗЛП методом искусственного базиса и значение целевой функции на этом плане:
![]() ;
;

Решение
Запишем ЗЛП в каноническом виде с неотрицательной правой частью.
![]() ;
;
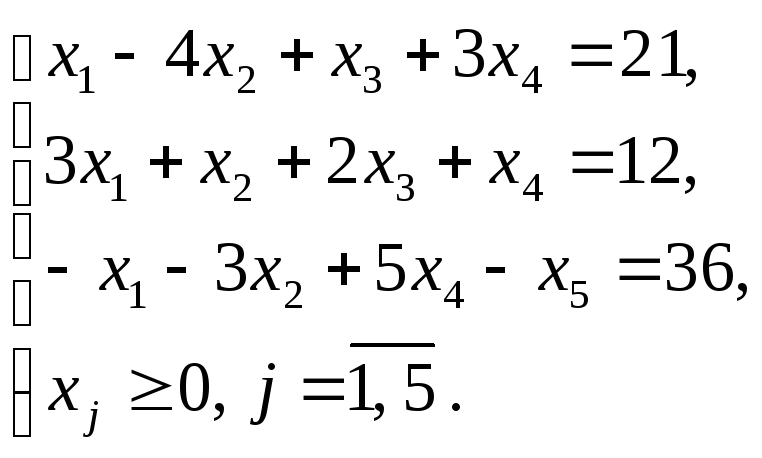
Составим М-задачу:
![]() ;
;
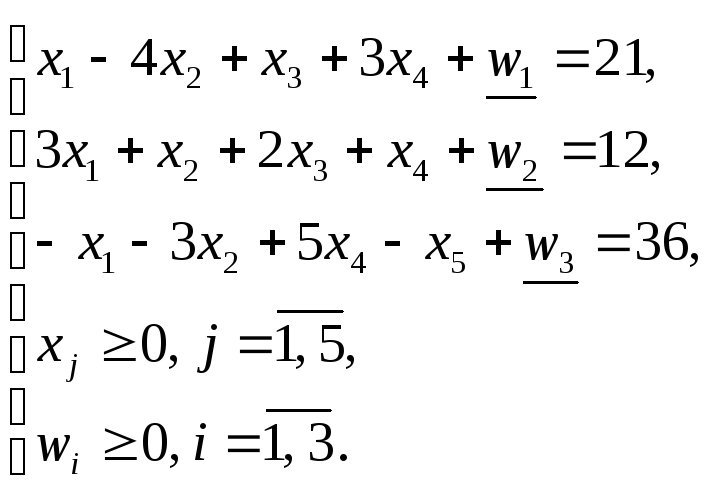
Тогда
начальный опорный план:
![]() ,
значение целевой функции на этом плане:
,
значение целевой функции на этом плане:![]() .
.
Пример 1.14
Найти начальный опорный план ЗЛП методом искусственного базиса и значение целевой функции на этом плане:
![]() ;
;
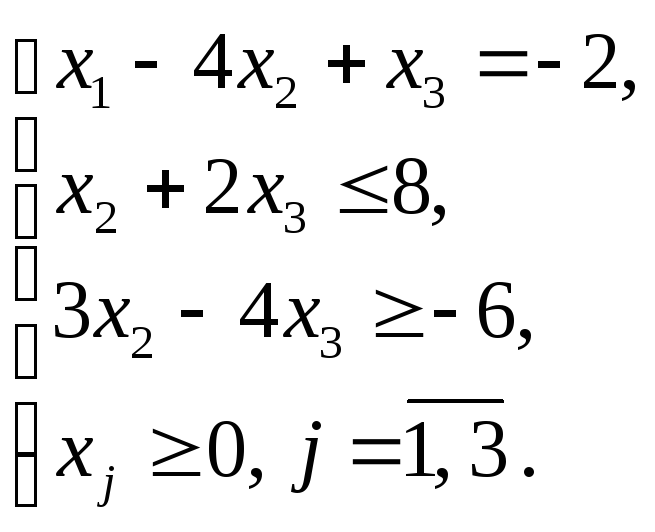
Решение
Запишем ЗЛП в каноническом виде с неотрицательной правой частью.
![]() ;
;
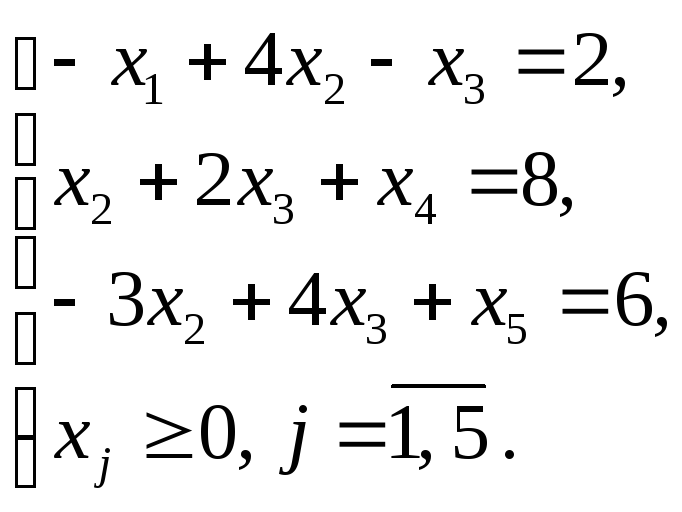
Составим М-задачу:
![]() ;
;

Тогда
начальный опорный план:
![]() ,
значение целевой функции на этом плане:
,
значение целевой функции на этом плане:![]() .
.
Пример 1.15
Найти начальный опорный план ЗЛП методом искусственного базиса и значение целевой функции на этом плане:
![]() ;
;

Решение
Запишем ЗЛП в каноническом виде с неотрицательной правой частью.
![]() ;
;

где
![]() .
.
Составим М-задачу:
![]() ;
;

где
![]() .
.
Тогда
начальный опорный план:
![]() ,
значение целевой функции на этом плане:
,
значение целевой функции на этом плане:![]() .
.
