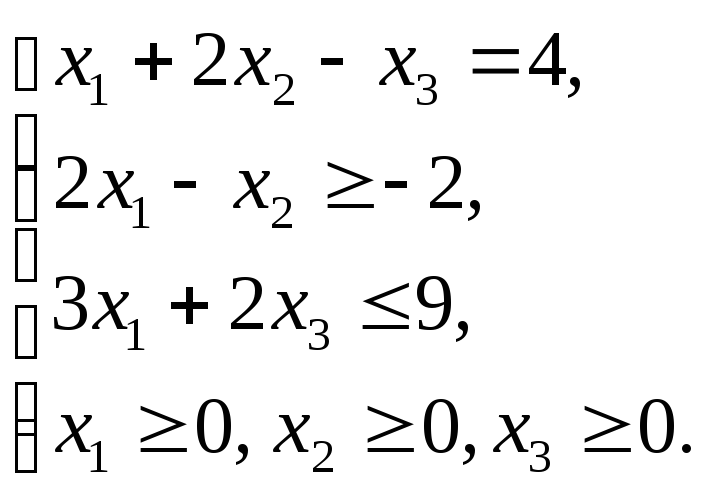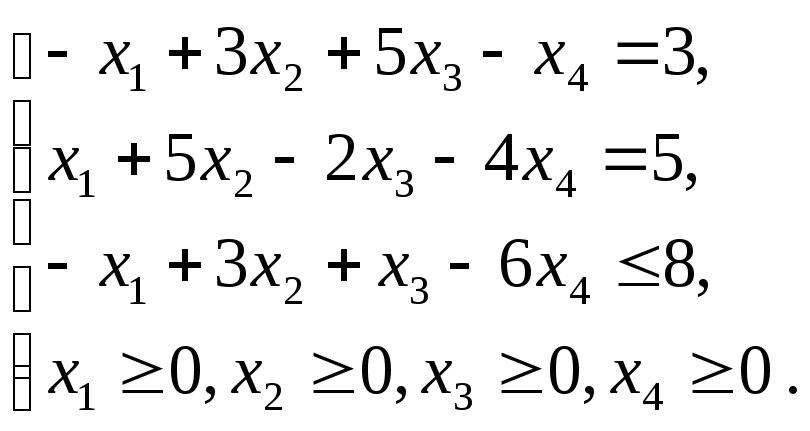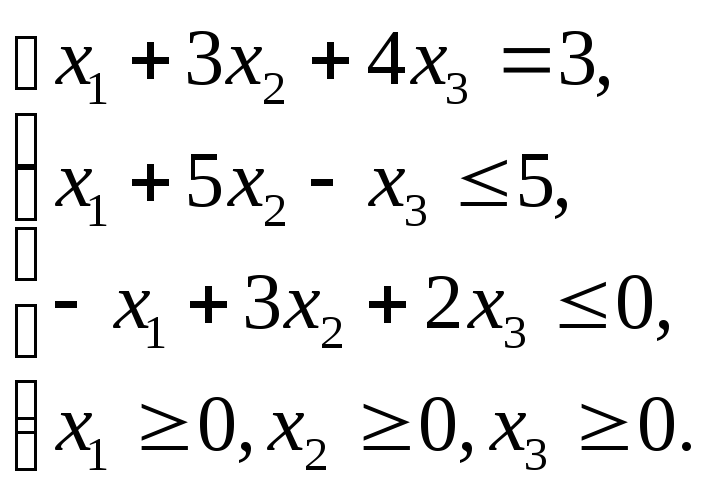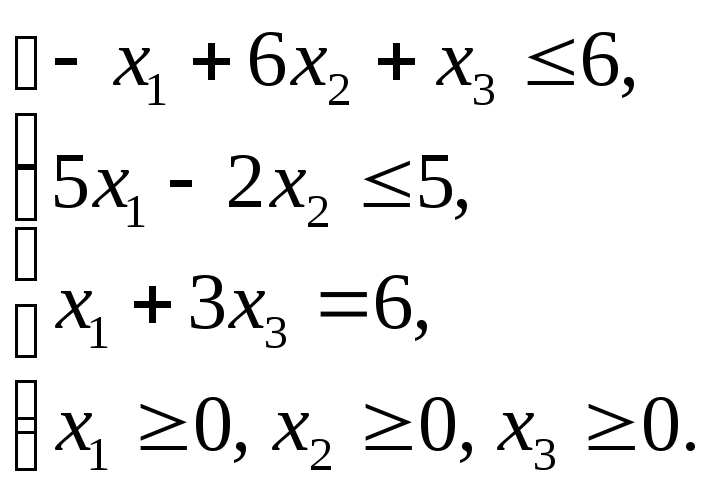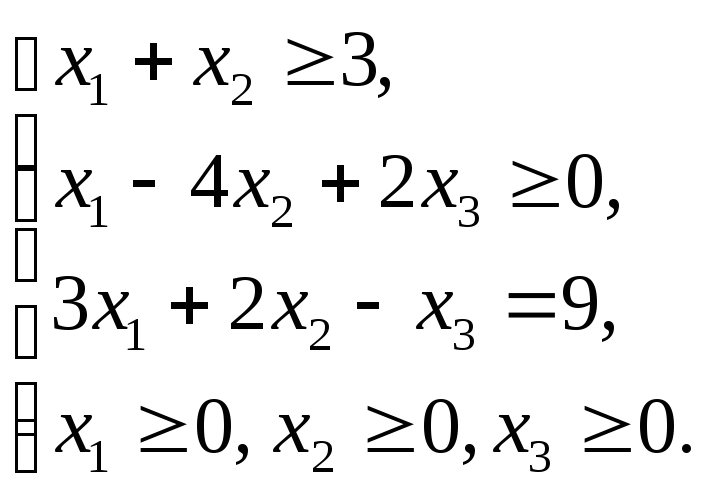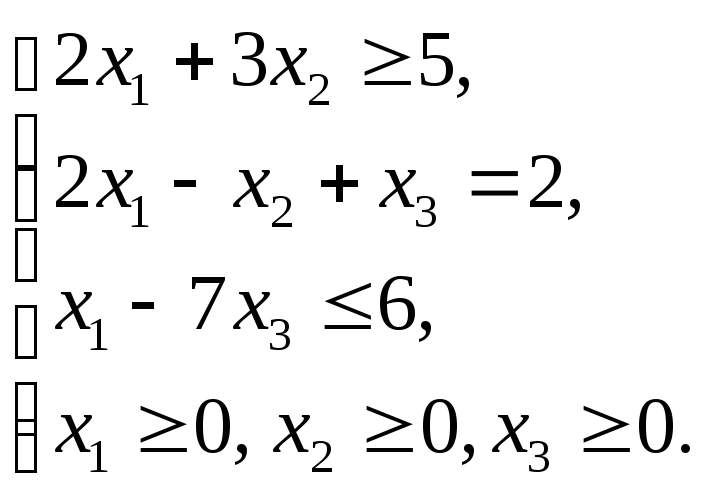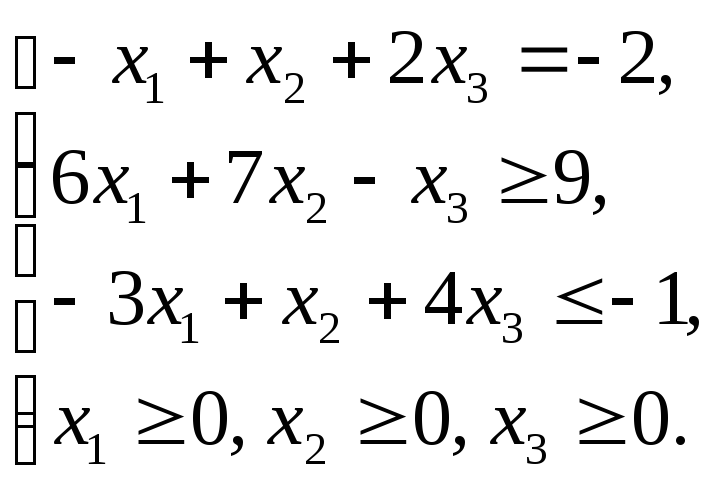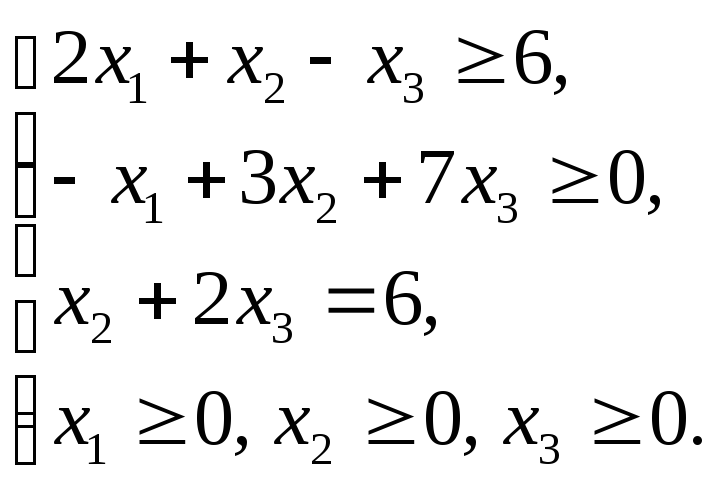1.4. Графический метод решения задач линейного программирования сnпеременными

Графическим методом решаются ЗЛП, если в ее канонической форме записи число переменных и число линейно независимых уравненийсвязаны соотношением.

Алгоритм графического метода решения ЗЛП со многими переменными (n>2)

1. Записать каноническую форму ЗЛП.

2. Выбрать две свободные переменные.

3. Выразить все остальные переменные через свободные, т.е. решить систему ограничений заданной задачи.

4. Выразить целевую функцию через свободные переменные.

5. Полученную двухмерную задачу решить графическим методом.

6. Найдя координаты оптимального решения двухмерной задачи, определяем остальные координаты оптимального решения исходной задачи.

7. Значение целевой функции на оптимальном плане двухмерной задачи совпадает со значением целевой функции на оптимальном плане исходной задачи.

Пример 1.11

Решим графически ЗЛП, математическая модель которой составлена в примере 1.2.

;

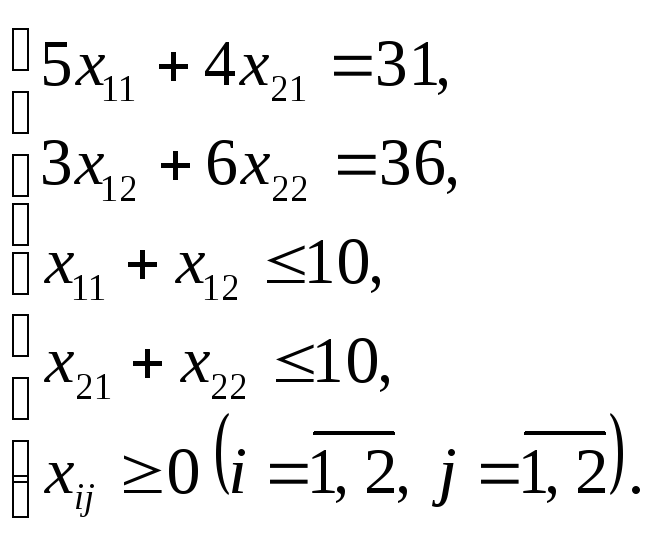
Решение

Перейдем к эквивалентной задаче с двумя переменными.

Математическую модель задачи представим в канонической форме записи:

;

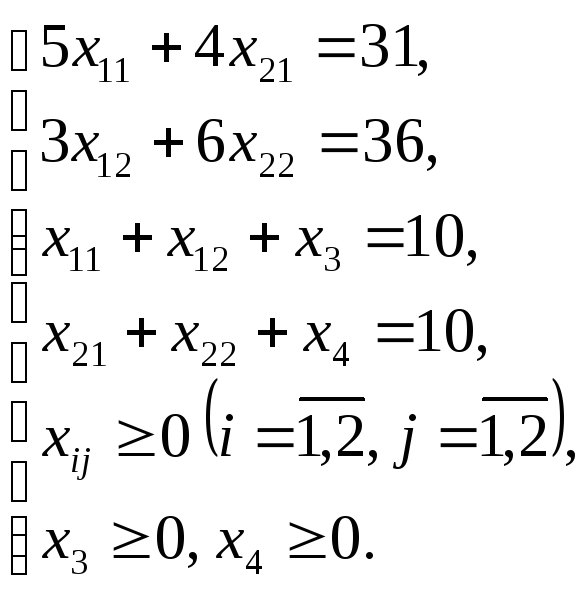
Пусть переменные ибудут свободными, а все остальные переменные базисными. Выразим все базисные переменные через свободные.

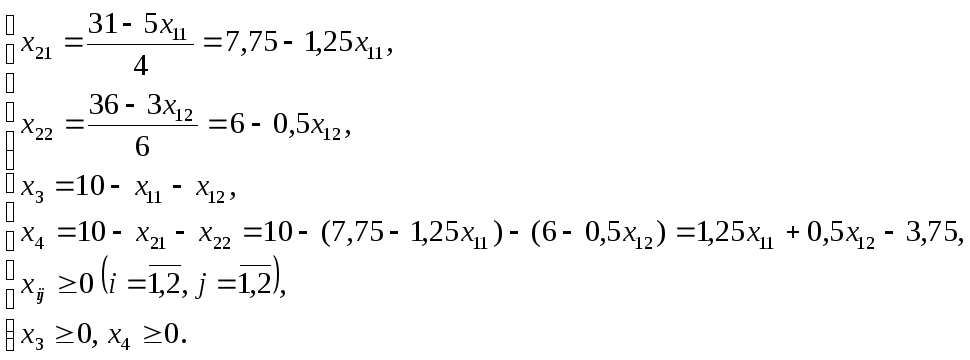
Выразим целевую функцию через свободные переменные.

Учитывая условия неотрицательности базовых переменных, получим эквивалентную задачу с двумя переменными:

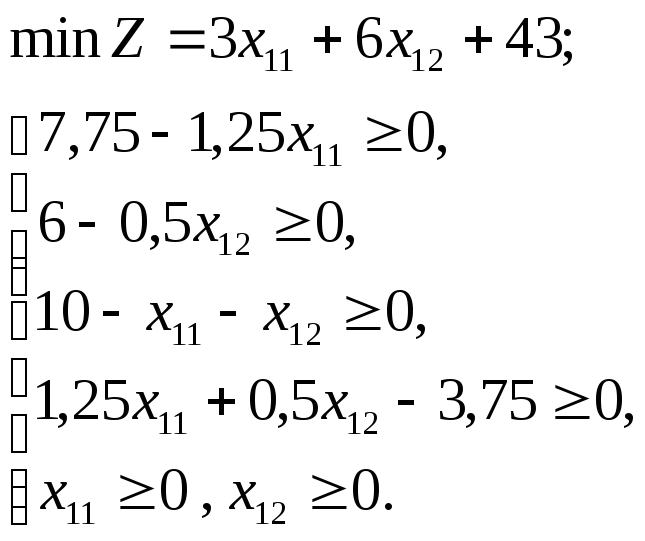или

Полученную двухмерную задачу решим графическим методом.

Построим ОДР задачи (Рис. 1.7). Для этого в системе координат на плоскости изобразим граничные прямые:

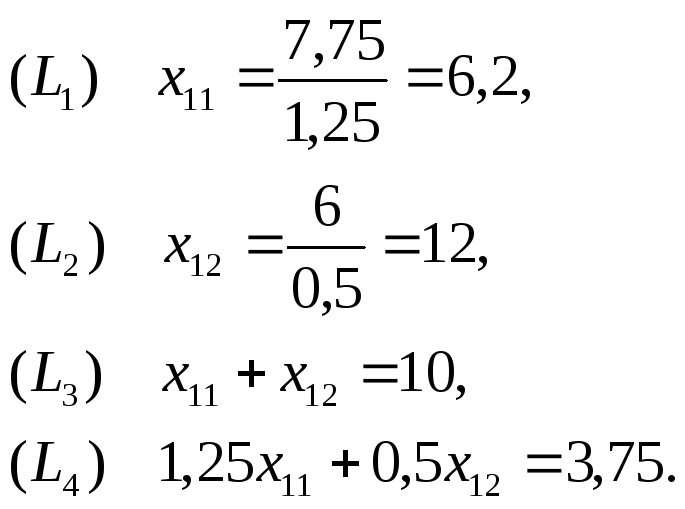
Затем определим, какую полуплоскость определяет соответствующее неравенство, подставив координаты какой-нибудь точки, не лежащей на данной прямой, например (0;0). Ограничения означают, что ОДР лежит вI четверти системы координат . Соответствующие полуплоскости на рисунке показаны стрелками. Пересечение указанных полуплоскостей и определяет ОДР данной задачи – это многоугольникABCDE.

Рис. 1.7

Строим вектор-градиент целевой функции =(3;6).

Оптимальное решение достигается в точке E(3;0).

Перейдем к решению исходной задачи. Т.е. найдем значения базисных переменных:

Итак, решение исходной задачи: ,.

Экономический смысл полученного решения задачи:

для того, чтобы затраты были минимальными и составили 52 усл. ден. ед. необходимо, чтобы оборудование А₁ выпускало 3 часа продукцию P₁, оборудование А₂ выпускало 4 часа продукцию P₁ и 6 часов продукцию P₂.

Преобразовать ЗЛП к эквивалентной двумерной ЗЛП можно и не записывая исходную задачу в канонической форме. Достаточно из ограничений-равенств системы выразить базисные переменные через выбранные две свободные и подставить это выражение всюду, где они встречаются в ограничениях-неравенствах и в целевой функции. Учитывая условия неотрицательности базисных переменных двумерная модель будет иметь то же количество ограничений, что и исходная. Таким образом, графическим методом можно решить лишь ту ЗЛП с n переменными, система ограничений которой имеет не менее n–2 линейно-независимых ограничений-равенств.

Пример 1.12

Решим графически ЗЛП:

;

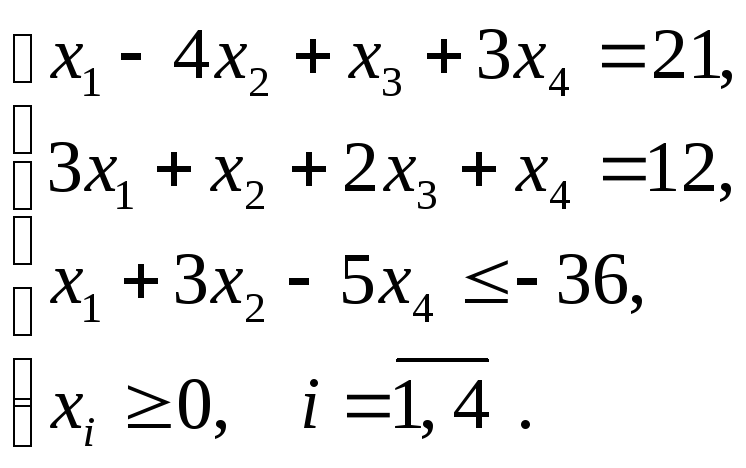
Решение

Перейдем к эквивалентной задаче с двумя переменными.

Пусть переменные ибудут свободными, а все остальные переменные базисными. Выразим все базисные переменные через свободные. Сделаем это последовательно. Сначала выразим, например, из второго ограничения-равенства базисную переменнуюи подставим это выражение всюду, где она встречается в модели:

;

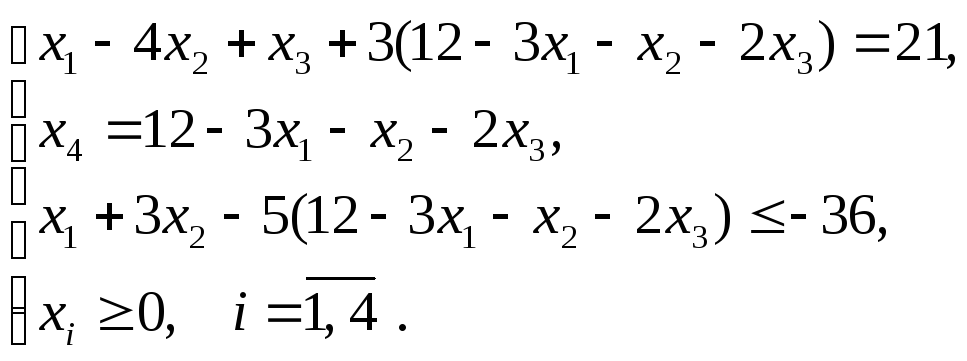
Раскрыв скобки, приведя подобные и учитывая условие неотрицательности переменной , получим следующую модель от трех переменных, эквивалентную исходной:

;

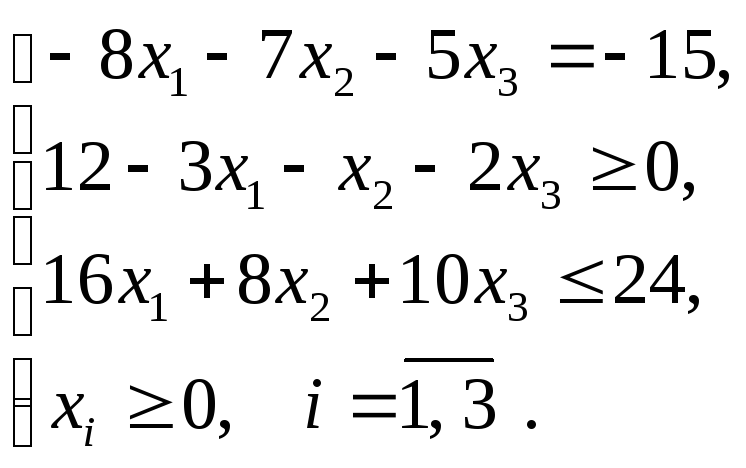
Затем выразим, например, из первого ограничения-равенства базисную переменную и подставим это выражение всюду, где она встречается в модели:

;

Раскрыв скобки, приведя подобные и учитывая условие неотрицательности переменной , получим следующую модель от двух переменных, эквивалентную исходной:

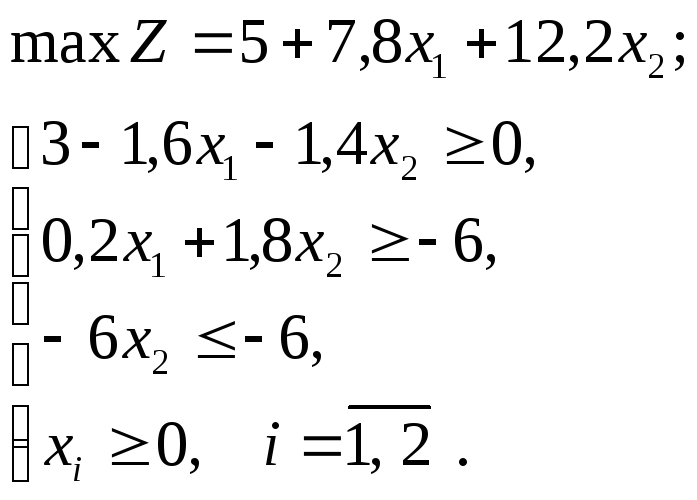или

Полученную двухмерную задачу решим графическим методом.

Построим ОДР задачи (Рис. 1.8). Для этого в системе координат на плоскости изобразим граничные прямые:

Затем определим, какую полуплоскость определяет соответствующее неравенство, подставив координаты какой-нибудь точки, не лежащей на данной прямой, например (0;0). Ограничения означают, что ОДР лежит вI четверти системы координат . Соответствующие полуплоскости на рисунке показаны стрелками. Пересечение указанных полуплоскостей и определяет ОДР данной задачи – это треугольникABC.

Вектор-градиент целевой функции =(7,8;12,2). Так как нас интересует направление вектора-градиента, а не его длина, то можно изобразить вектор=(3,9;6,1)=0,5, который в два раза меньше вектора градиента.

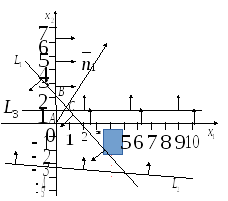
Рис. 1.8

Оптимальное решение достигается в точке В, которая лежит на пересечении прямой и оси. Для определения ее координат необходимо решить систему уравнений:

Откуда . Таким образом,. Подставив значениеив целевую функциюZ, получаем:

.

Перейдем к решению исходной задачи. Т.е. найдем значения базисных переменных:

,

.

Итак, решение исходной задачи: ,.

Задачи

Решить ЗЛП графическим методом (1.4.1 – 1.4.8)

1.4.1 ; 1.4.3 ; 1.4.5 ; 1.4.7 ;

1.4.2 ; 1.4.4 ; 1.4.6 ; 1.4.8 ;

1.4.9 – 1.4.11

Решить задачи 1.1.4, 1.1.9, 1.1.11 (соответственно) графическим методом.