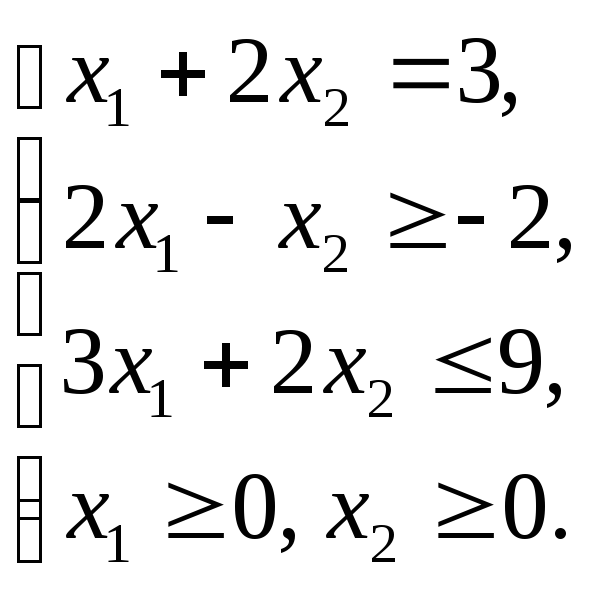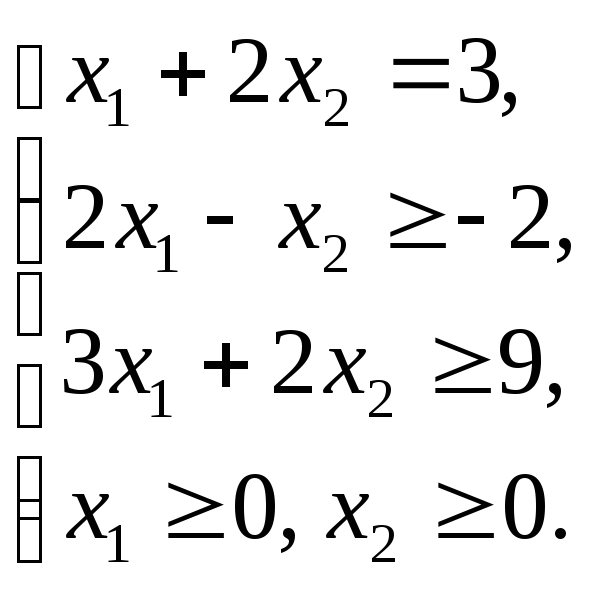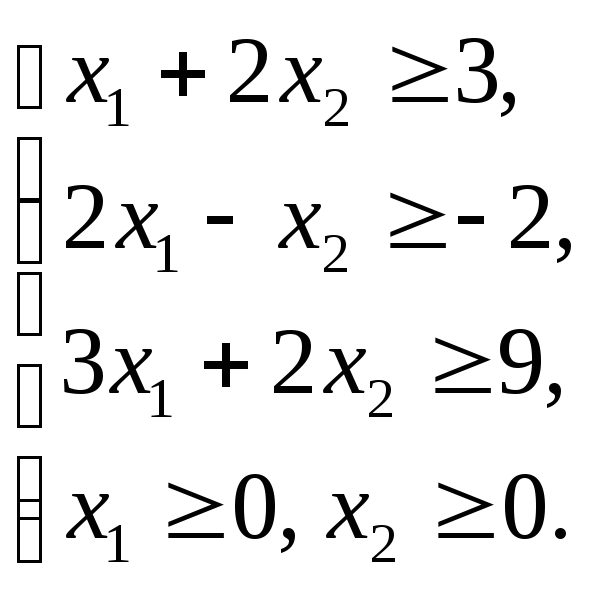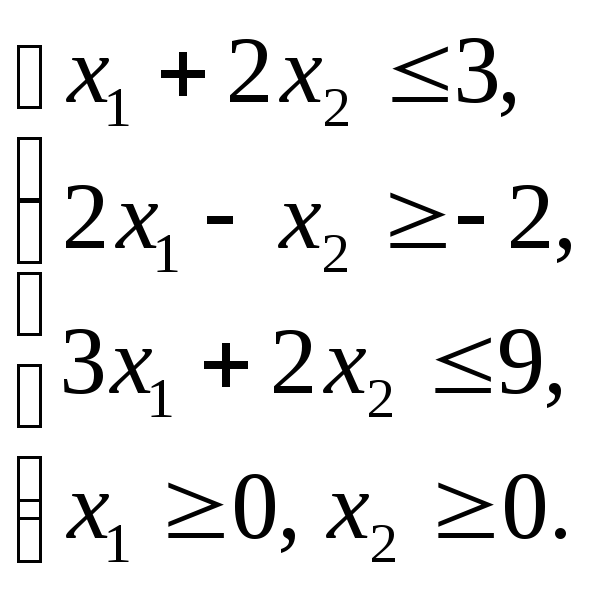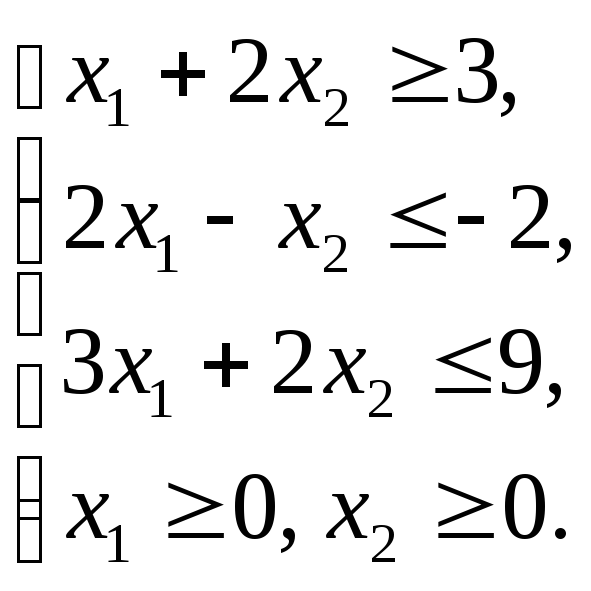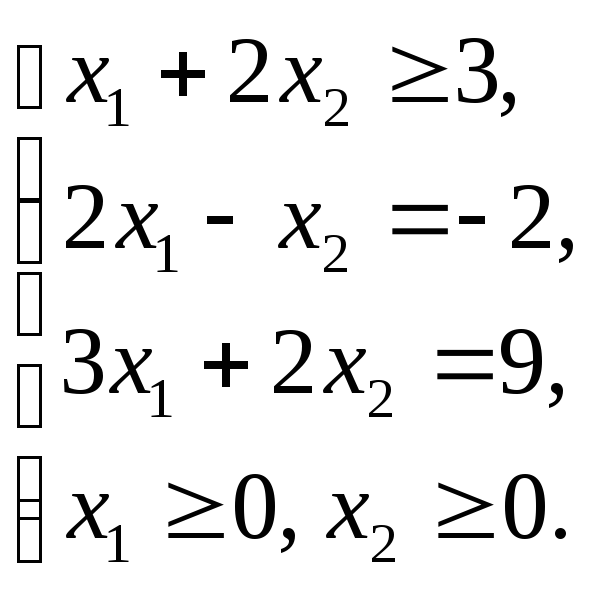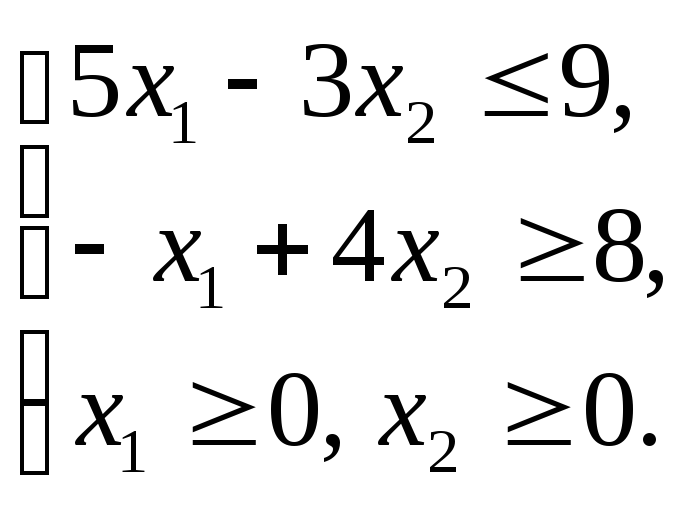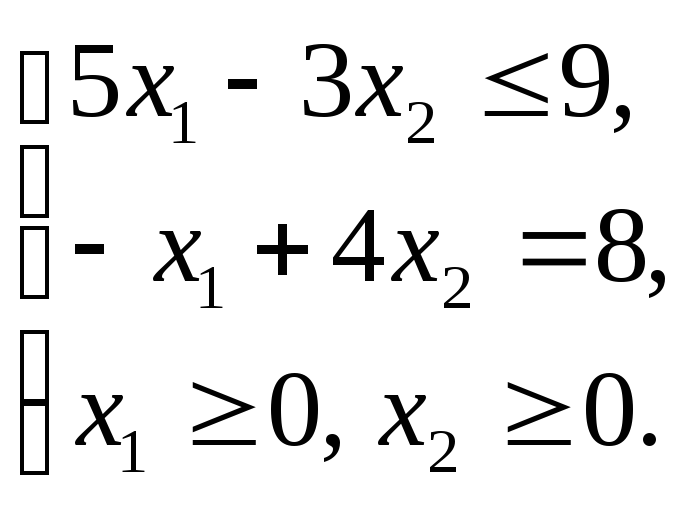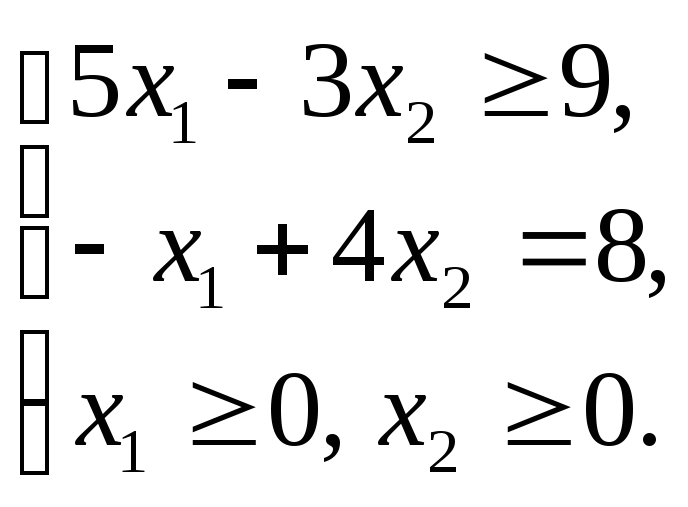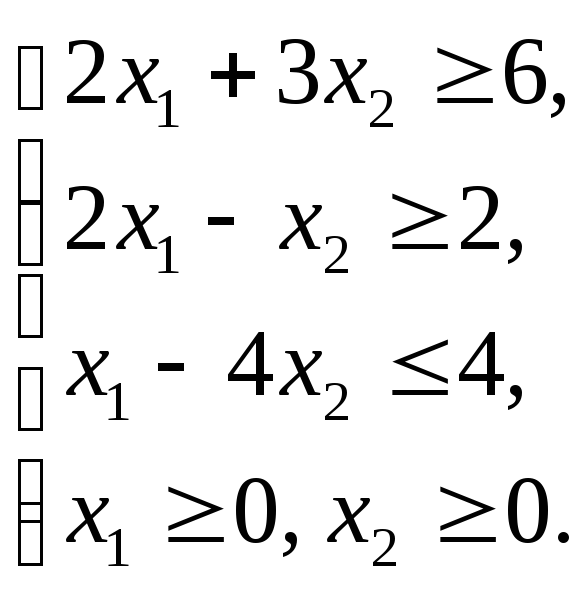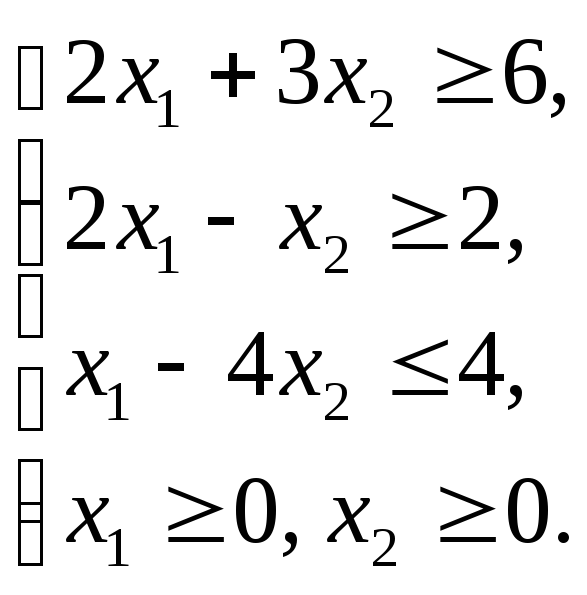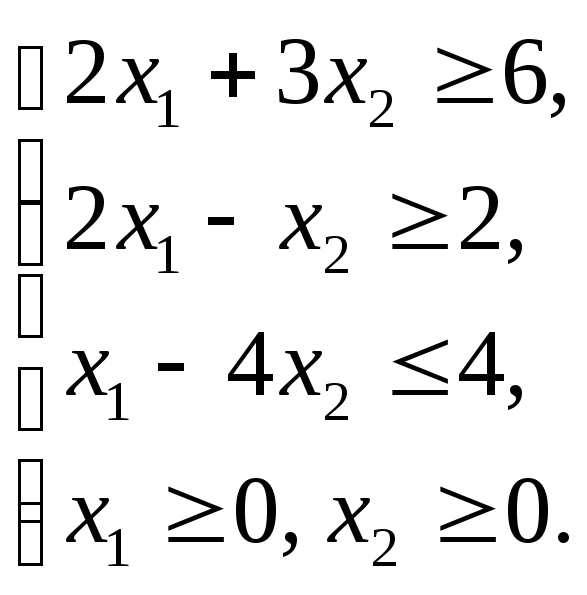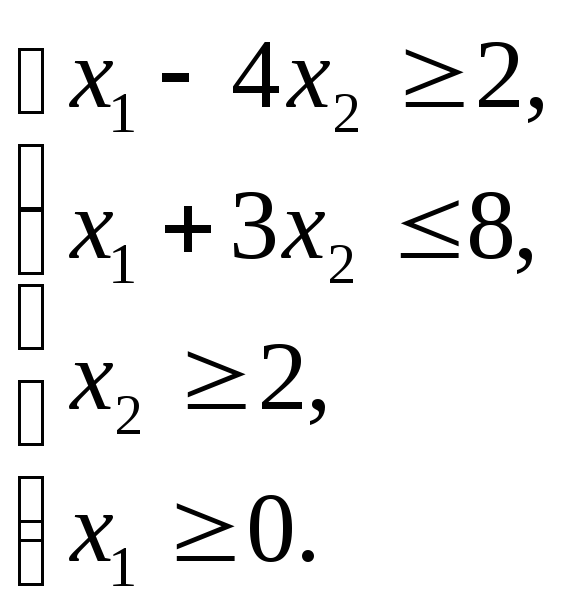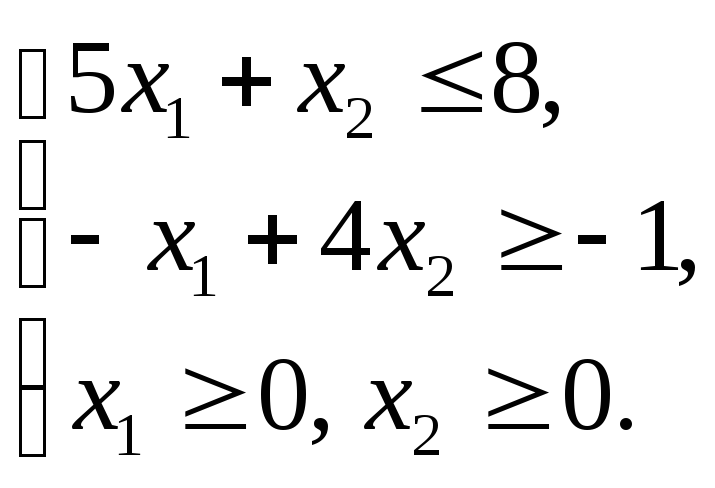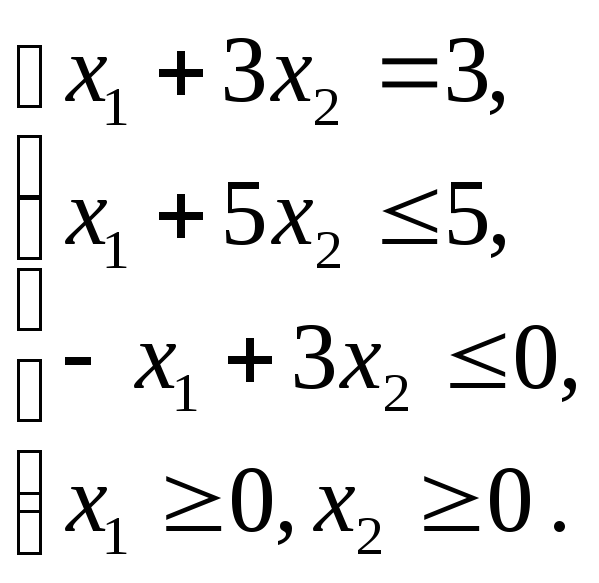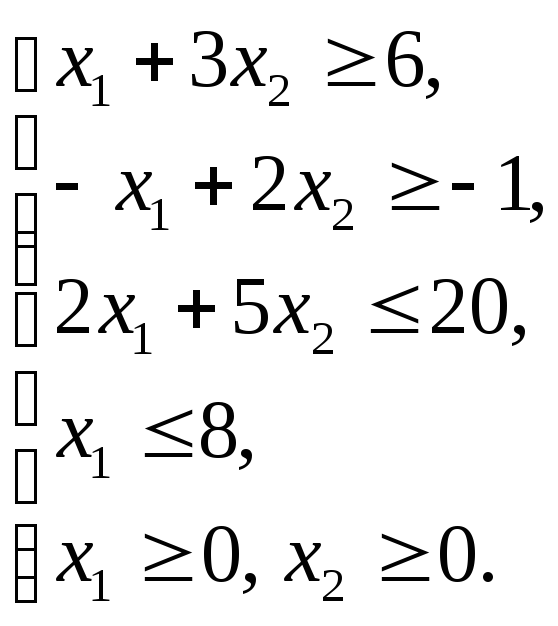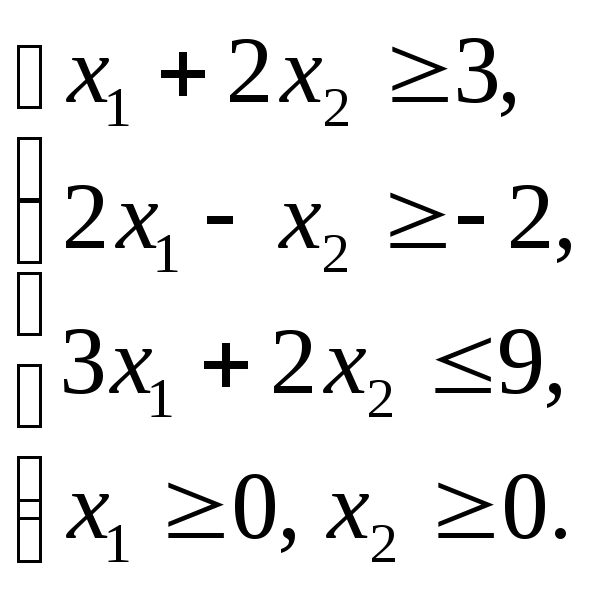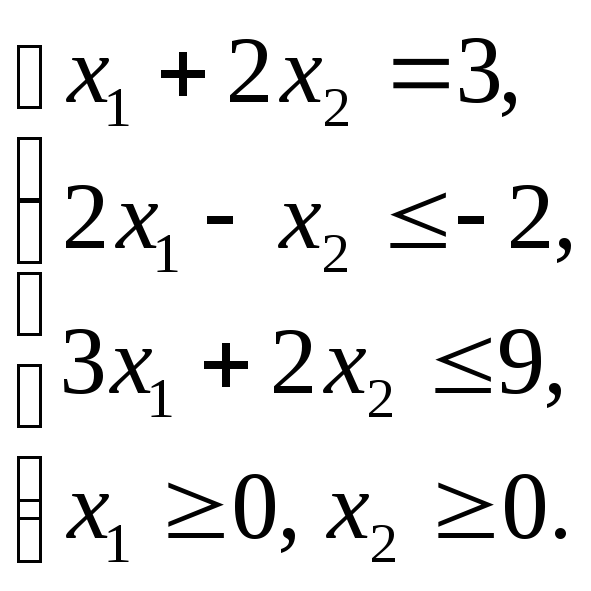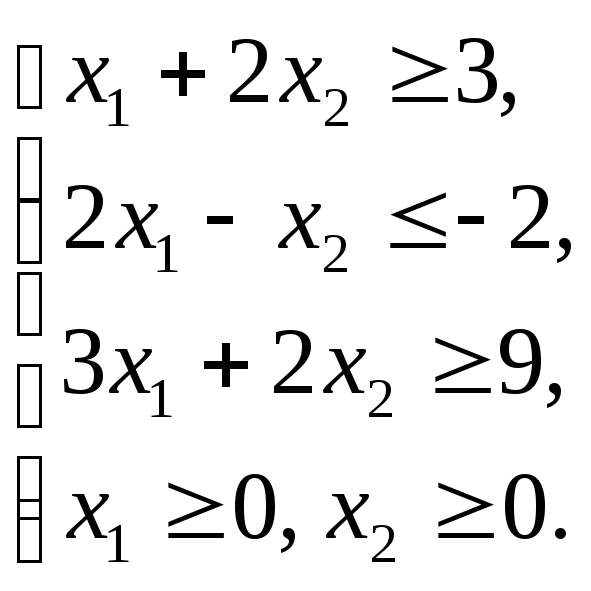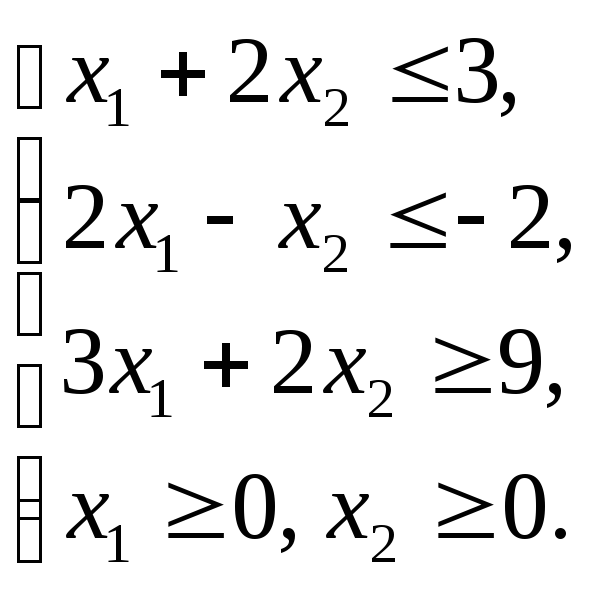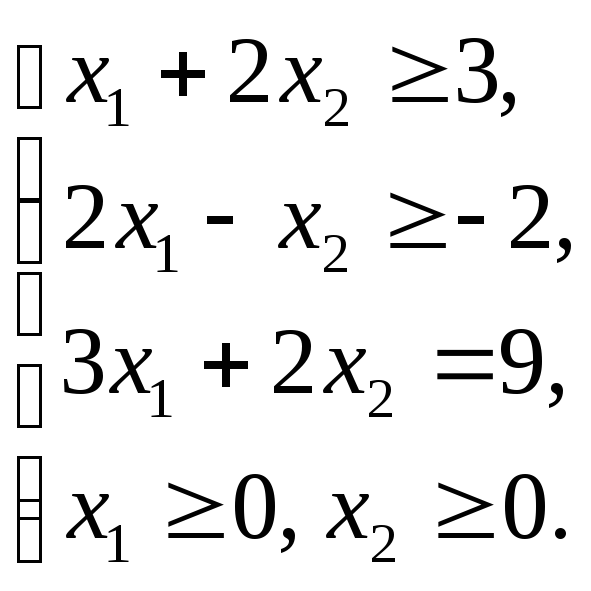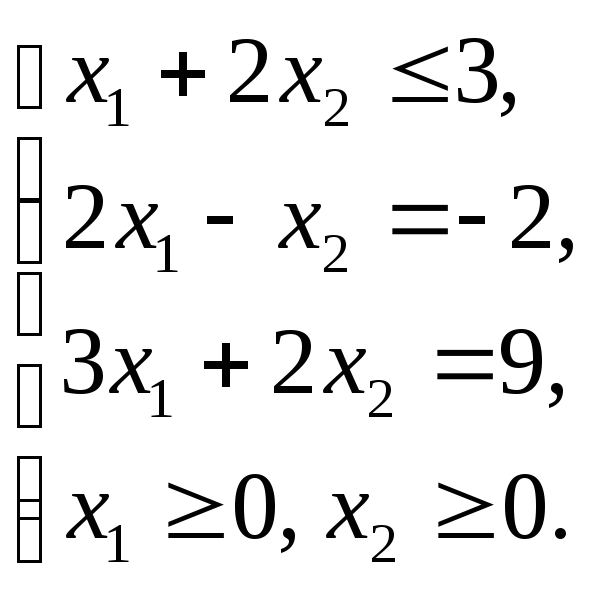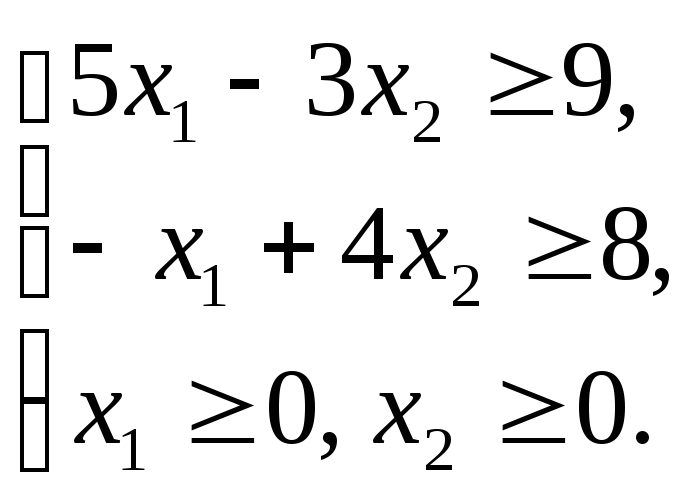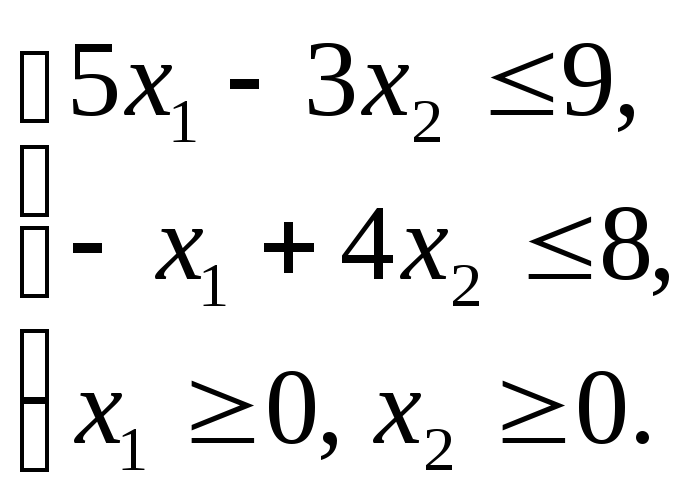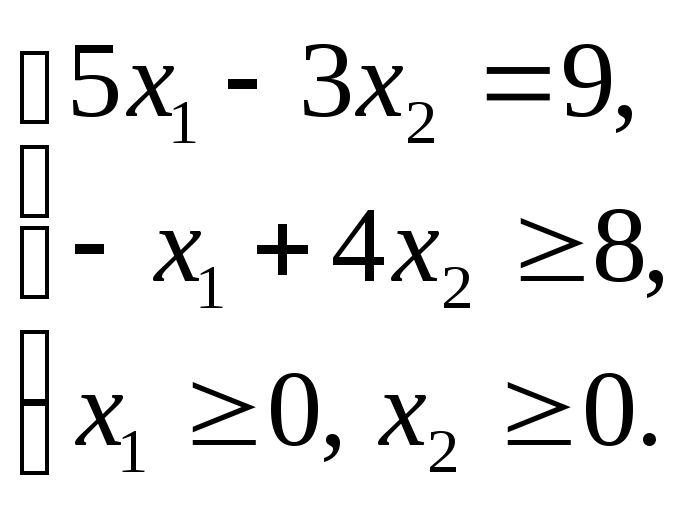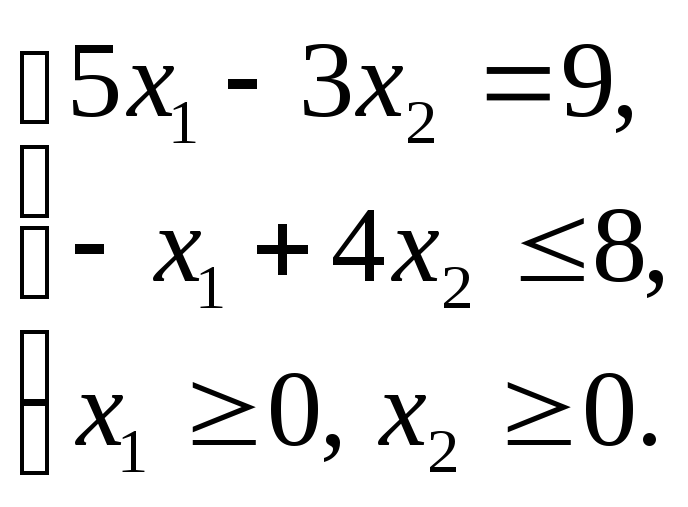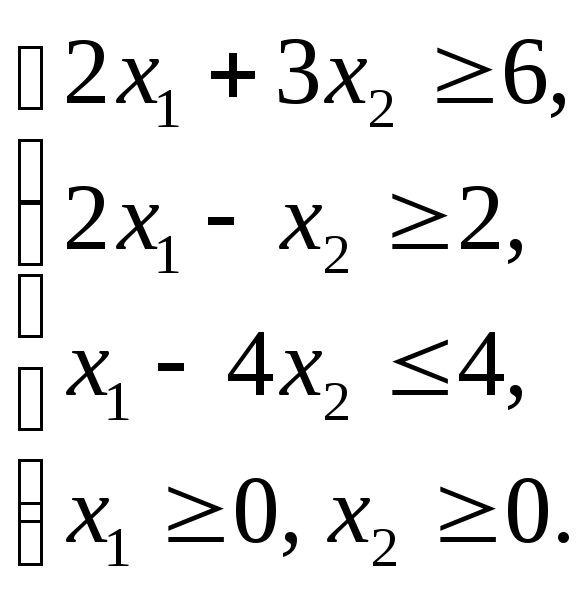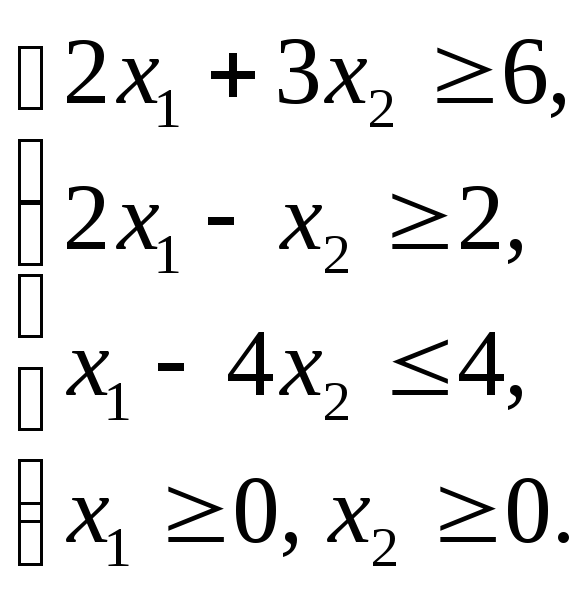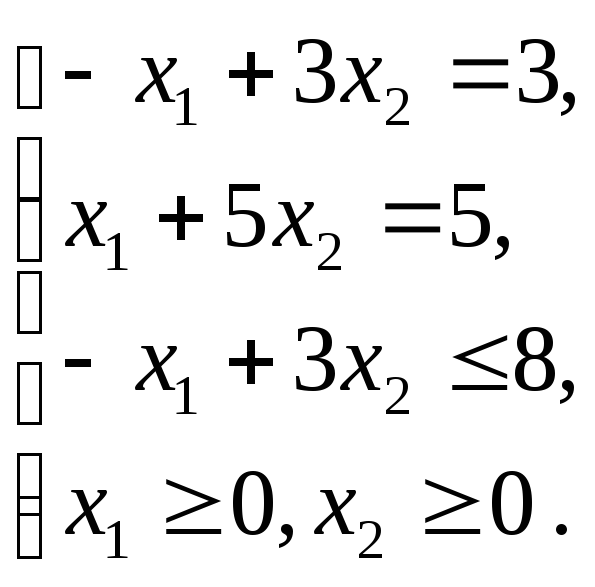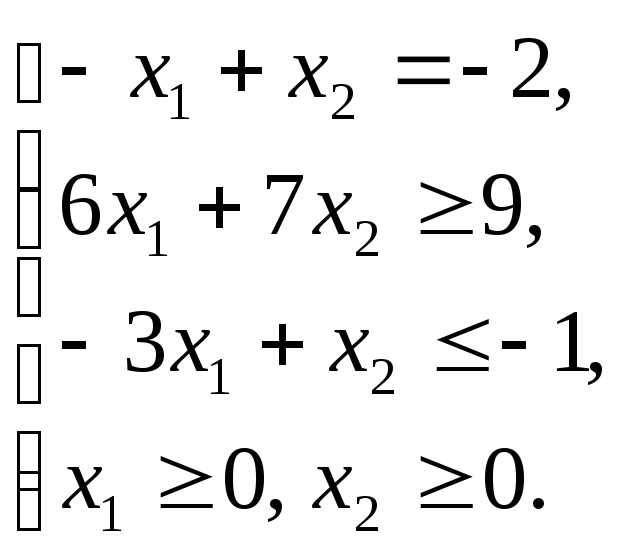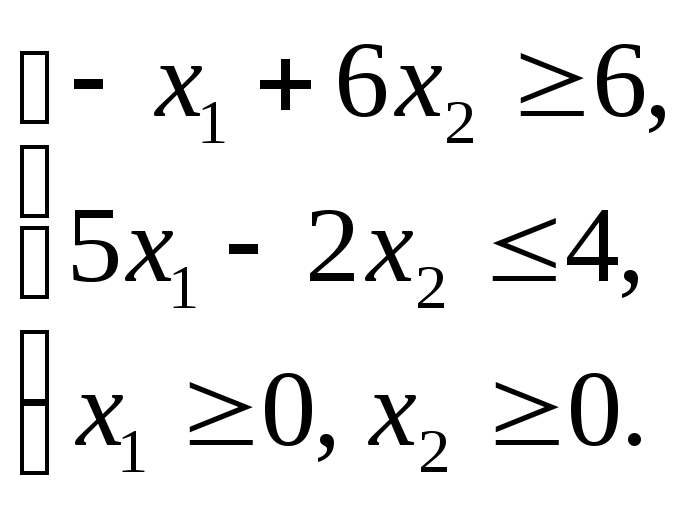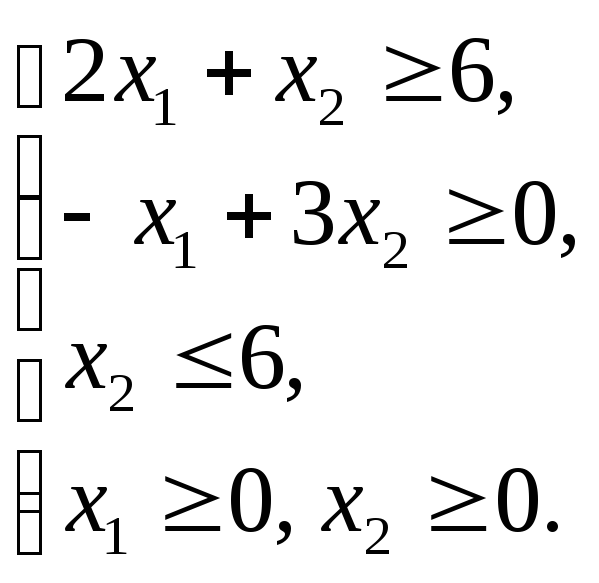- •Глава 1. Линейное программирование 3
- •Глава 2. Транспортная задача линейного программирования (тз) 68
- •Глава 3. Динамическое программирование 98
- •Глава 1. Линейное программирование
- •1.1. Математическая модель задачи линейного программирования
- •1.2. Формы записи задач линейного программирования
- •Рассмотрим приемы, позволяющие переходить от одной формы записи задачи к другой
- •1.3. Геометрическая интерпретация и графический метод решения задач линейного программирования с двумя переменными
- •Алгоритм графического метода решения злп с двумя переменными
- •1.4. Графический метод решения задач линейного программирования сnпеременными
- •1.5. Симплексный метод решения задач линейного программирования
- •Алгоритм решения злп симплексным методом
- •Нахождение начального опорного плана злп ( )
- •Нахождение начального опорного плана злп методом искусственного базиса
- •Нахождение начального опорного плана злп методом Жордановых исключений
- •Шаг Жордановых исключений осуществляется по следующим правилам:
- •Исследование на оптимальность опорного плана при решении злп на
- •Переход к новому опорному плану
- •1.6. Двойственные задачи линейного программирования
- •Правила построения двойственной задачи.
- •Глава 2. Транспортная задача линейного программирования (тз)
- •2.1. Математическая модель транспортной задачи
- •Закрытая и открытая модели транспортной задачи
- •2.2. Решение транспортной задачи
- •Алгоритм решения транспортной задачи
- •Нахождение начального опорного плана методом «минимального элемента»
- •Нахождение начального опорного плана методом «северо-западного угла»
- •Нахождение начального опорного плана методом Фогеля
- •Проверка на оптимальность невырожденного опорного плана методом потенциалов
- •Переход к новому опорному плану
- •Цикл пересчета
- •Глава 3. Динамическое программирование
- •3.1. Задача оптимального распределения ресурсов
- •I этап. Условная оптимизация.
- •II этап. Безусловная оптимизация.
- •3.2. Задача об оптимальной стратегии замены оборудования
- •I этап. Условная оптимизация.
- •II этап. Безусловная оптимизация.
- •Список использованной литературы
1.3. Геометрическая интерпретация и графический метод решения задач линейного программирования с двумя переменными
Графическим методом можно решать любые задачи линейного программирования с двумя переменными.
Пусть дана задача
![]()
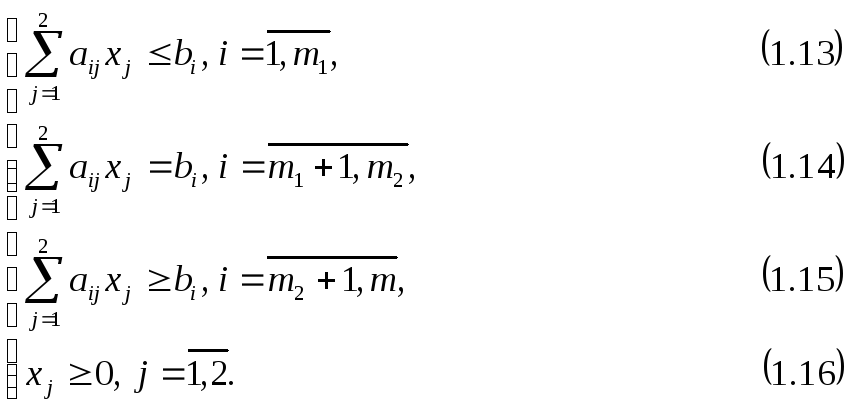
где ![]() – заданные действительные числа.
– заданные действительные числа.
Дадим геометрическую интерпретацию элементов этой задачи.
Каждое
из ограничений-неравенств (1.13,1.15,1.16)
системы задает на плоскости
![]() некоторую полуплоскость. Каждое из
ограничений-равенств (1.14) системы задает
на плоскости
некоторую полуплоскость. Каждое из
ограничений-равенств (1.14) системы задает
на плоскости![]() некоторую прямую. И полуплоскость и
прямая – выпуклые множества. Т.к.
пересечение любого числа выпуклых
множеств является выпуклым множеством,
то область допустимых решений (ОДР)
задачи является выпуклым множеством.
некоторую прямую. И полуплоскость и
прямая – выпуклые множества. Т.к.
пересечение любого числа выпуклых
множеств является выпуклым множеством,
то область допустимых решений (ОДР)
задачи является выпуклым множеством.
Целевая
функция – это семейство параллельных
прямых, называемых линиями
уровня целевой функции.
Вектор-градиент целевой функции
![]() показывает направление ее наискорейшего
возрастания и перпендикулярен линиям
уровня целевой функции.
показывает направление ее наискорейшего
возрастания и перпендикулярен линиям
уровня целевой функции.
Опорной прямой называется линия уровня, которая имеет хотя бы одну общую точку с областью допустимых решений и по отношению к которой эта область находится в одной из полуплоскостей.
Область допустимых решений любой задачи имеет не более двух опорных прямых, на одной из которых может находиться оптимальное решение (рис. 1.1 – 1.2).

Рис. 1.1
Алгоритм графического метода решения злп с двумя переменными
Построить область допустимых решений.
Если область допустимых решений является пустым множеством, то задача не имеет решения вследствие несовместности системы ограничений.
Если область допустимых решений является непустым множеством, построить вектор-градиент целевой функции.
Произвольную линию уровня, имеющую общие точки с ОДР, перемещаем параллельно самой себе до опорной прямой в направлении вектора-градиента (при решении задачи на
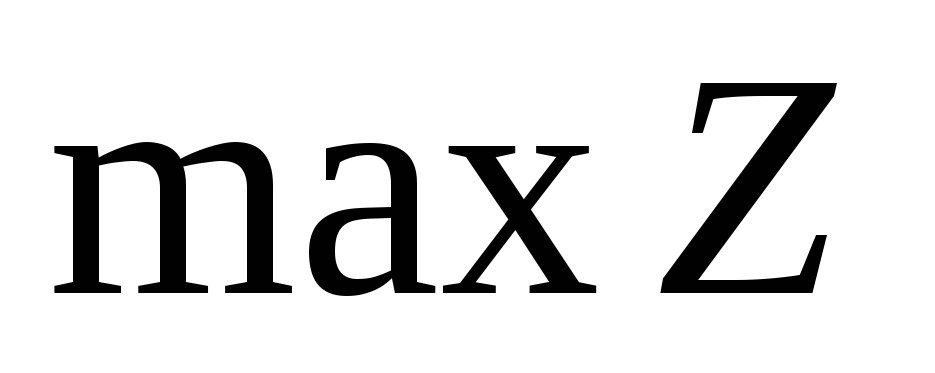 )
или в противоположном направлении (при
решении задачи на
)
или в противоположном направлении (при
решении задачи на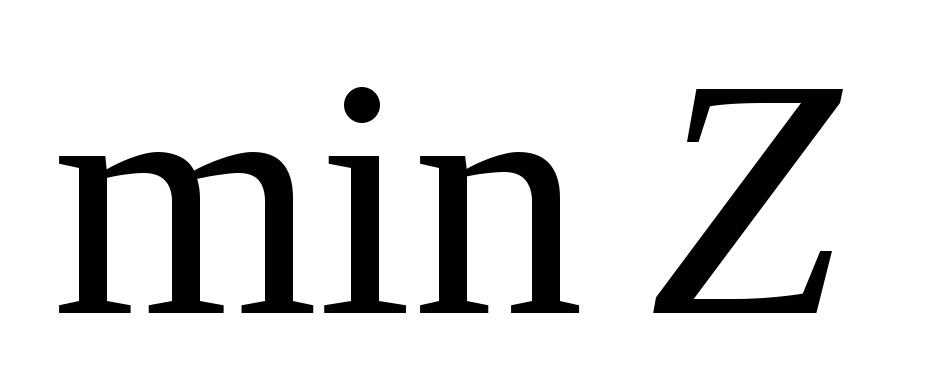 ).
).Если при перемещении линии уровня по ОДР в направлении, соответствующем приближению к экстремуму целевой функции, линия уровня уходит в бесконечность, то задача не имеет решения вследствие неограниченности целевой функции.
Если ЗЛП имеет оптимальное решение, то для его нахождения решить совместно уравнения прямых, ограничивающих ОДР и имеющих общие точки с соответствующей опорной прямой. Если целевая функция задачи достигает экстремума в двух вершинах ОДР, то она достигает экстремума также в любой точке, лежащей на отрезке, соединяющем эти две вершины. Задача имеет бесконечное множество оптимальных решений.
Вычислить значение целевой функции на оптимальном решении.
Пример 1.6
Решим графически ЗЛП, математическая модель которой составлена в примере 1.3.
![]() ;
;

Вначале
построим ОДР задачи (рис. 1.2). Для этого
в системе координат
![]() на плоскости изобразим граничные прямые:
на плоскости изобразим граничные прямые:
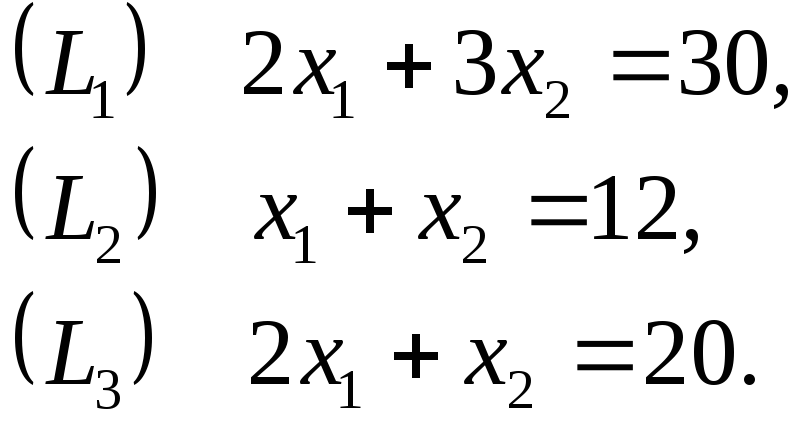

Рис. 1.2
Затем
определим, какую полуплоскость определяет
соответствующее неравенство, подставив
координаты какой-нибудь точки, не лежащей
на данной прямой, например (0;0). Ограничения
(1.17) означают, что ОДР лежит в I
четверти системы координат
![]() .
Соответствующие полуплоскости на
рисунке показаны стрелками. Пересечение
указанных полуплоскостей и определяет
ОДР данной задачи.
.
Соответствующие полуплоскости на
рисунке показаны стрелками. Пересечение
указанных полуплоскостей и определяет
ОДР данной задачи.
Строим
вектор-градиент целевой функции
![]() =(5;4).
=(5;4).
Строим
произвольную линию уровня, например
![]() ,
проходящую через начало координат и
перемещаем ее параллельно самой себе
в направлении вектора
,
проходящую через начало координат и
перемещаем ее параллельно самой себе
в направлении вектора![]() по
ОДР (рис. 1.2). Последняя точка соприкосновения
прямой
по
ОДР (рис. 1.2). Последняя точка соприкосновения
прямой
![]() с ОДР и есть оптимальное решение – это
точка С.
с ОДР и есть оптимальное решение – это
точка С.
Точка
![]() лежит на пересечении прямых
лежит на пересечении прямых![]() и
и![]() .
Для определения ее координат необходимо
решить систему уравнений:
.
Для определения ее координат необходимо
решить систему уравнений:
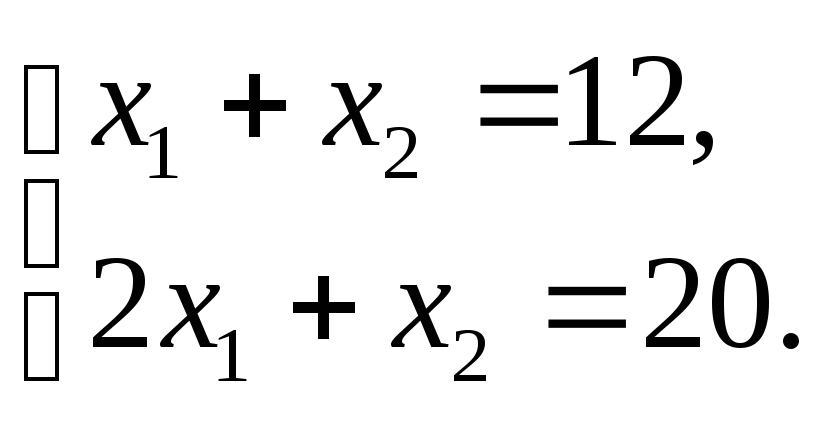
Откуда
![]() .
Таким образом,
.
Таким образом,![]() .
Подставив значение
.
Подставив значение![]() и
и![]() в целевую функциюZ,
получаем:
в целевую функциюZ,
получаем:
![]() .
.
Таким образом, для того, чтобы получить максимальную прибыль в размере 56 ден. ед., необходимо запланировать выпуск 8 ед. продукции вида П1 и 4 ед. продукции П2.
Пример 1.7
Графическим методом решить ЗЛП:
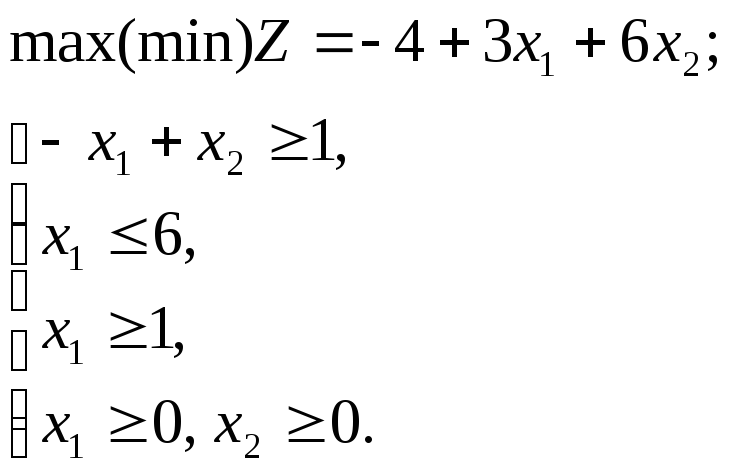
Решение
Вначале
построим ОДР задачи (рис. 1.3). Для этого
в системе координат
![]() на плоскости изобразим граничные прямые:
на плоскости изобразим граничные прямые:
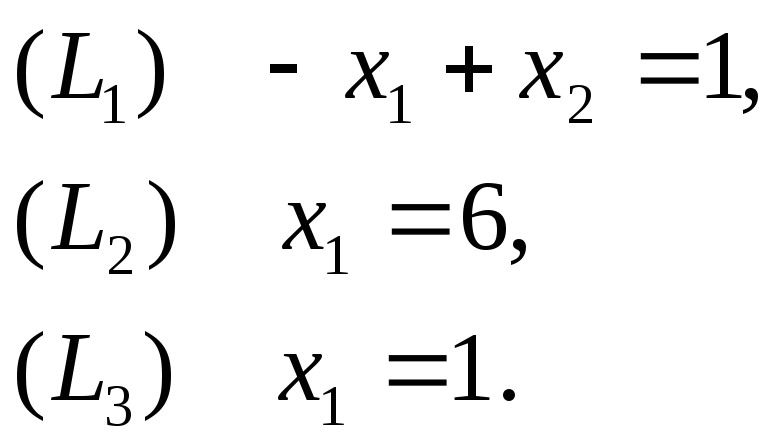
Затем
определим, какую полуплоскость определяет
соответствующее неравенство, подставив
координаты какой-нибудь точки, не лежащей
на этой прямой. Ограничения
![]() означают, что ОДР лежит вI
четверти системы координат
означают, что ОДР лежит вI
четверти системы координат
![]() .
Соответствующие полуплоскости на
рисунке показаны стрелками. Пересечение
указанных полуплоскостей и определяет
ОДР данной задачи – это открытая
многоугольная областьABCD.
.
Соответствующие полуплоскости на
рисунке показаны стрелками. Пересечение
указанных полуплоскостей и определяет
ОДР данной задачи – это открытая
многоугольная областьABCD.
Строим
вектор-градиент целевой функции
![]() =(3;6).
Берем произвольную линию уровня целевой
функции (на рисунке она обозначена
пунктирной линией) и перемещаем ее в
направлении вектора-градиента до
последней точки соприкосновения с ОДР
для определения оптимального решения
на
=(3;6).
Берем произвольную линию уровня целевой
функции (на рисунке она обозначена
пунктирной линией) и перемещаем ее в
направлении вектора-градиента до
последней точки соприкосновения с ОДР
для определения оптимального решения
на![]() ,
при этом линия уровня уходит в
бесконечность, следовательно, на
,
при этом линия уровня уходит в
бесконечность, следовательно, на![]() задача не имеет решения вследствие
неограниченности целевой функции. Затем
перемещаем линию уровня в направлении,
противоположном вектору-градиенту до
последней точки соприкосновения с ОДР
для определения оптимального решения
на
задача не имеет решения вследствие
неограниченности целевой функции. Затем
перемещаем линию уровня в направлении,
противоположном вектору-градиенту до
последней точки соприкосновения с ОДР
для определения оптимального решения
на![]() .
Оптимальным решением на
.
Оптимальным решением на![]() является точка В, которая лежит на
пересечении прямых
является точка В, которая лежит на
пересечении прямых![]() и
и![]() .
Для определения ее координат необходимо
решить систему уравнений:
.
Для определения ее координат необходимо
решить систему уравнений: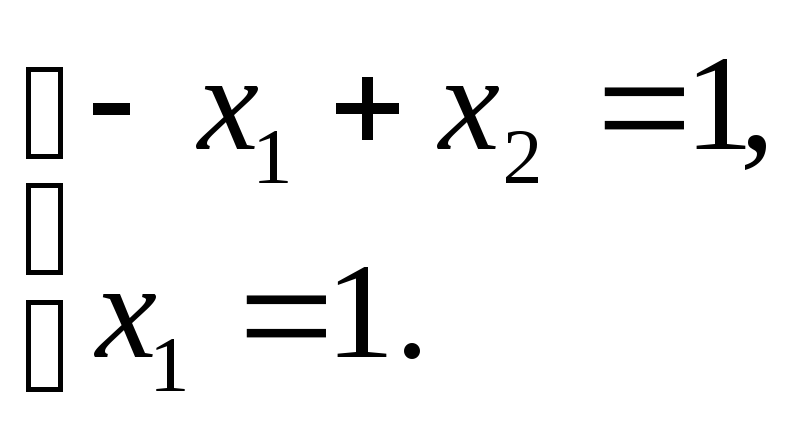
Откуда
![]() .
Таким образом,
.
Таким образом,![]() .
Подставив значение
.
Подставив значение![]() и
и![]() в целевую функциюZ,
получаем:
в целевую функциюZ,
получаем:
![]() .
.

Рис. 1.3
Ответ:
![]() .
.
Пример 1.8
Графическим методом решить ЗЛП:
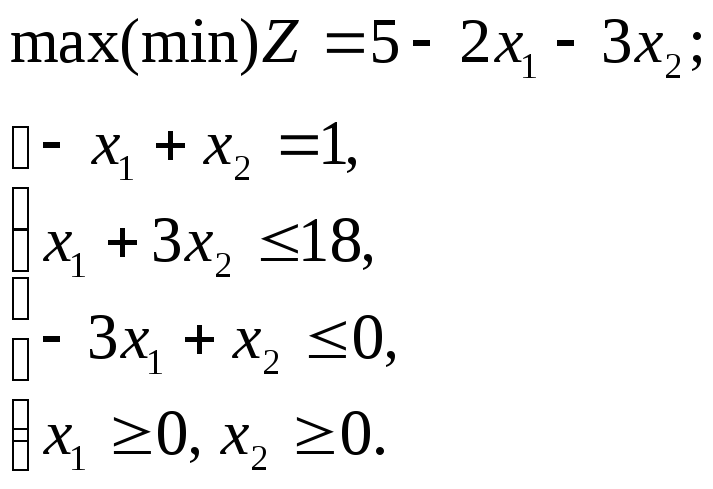
Решение
Вначале
построим ОДР задачи (рис. 1.4). Для этого
в системе координат
![]() на плоскости изобразим граничные прямые:
на плоскости изобразим граничные прямые:
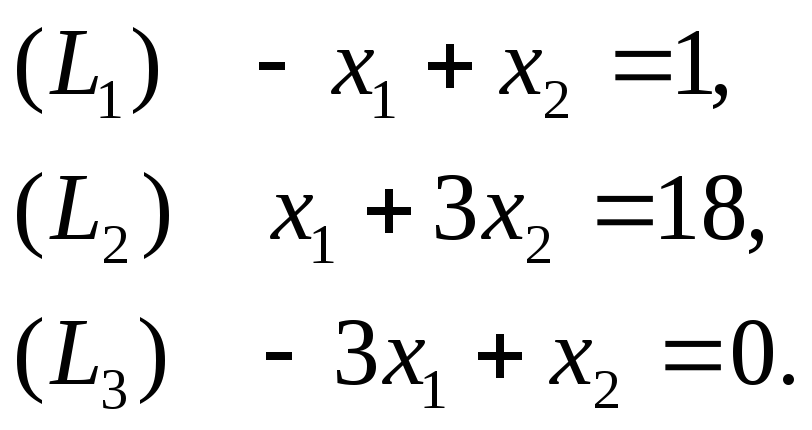

Рис. 1.4
Затем
определим, какую полуплоскость определяет
соответствующее неравенство, подставив
координаты какой-нибудь точки, не лежащей
на этой прямой. Ограничение-равенство
– это есть сама граничная прямая.
Ограничения
![]() означают, что ОДР лежит вI
четверти системы координат
означают, что ОДР лежит вI
четверти системы координат
![]() .
Соответствующие полуплоскости на
рисунке показаны стрелками. Пересечение
указанных полуплоскостей и прямой
.
Соответствующие полуплоскости на
рисунке показаны стрелками. Пересечение
указанных полуплоскостей и прямой![]() определяет ОДР данной задачи – это
отрезокAB.
определяет ОДР данной задачи – это
отрезокAB.
Строим
вектор-градиент целевой функции
![]() =(–2;–3).
Берем произвольную линию уровня целевой
функции (на рисунке она обозначена
пунктирной линией) и перемещаем ее в
направлении вектора-градиента до
последней точки соприкосновения с ОДР
для определения оптимального решения
на
=(–2;–3).
Берем произвольную линию уровня целевой
функции (на рисунке она обозначена
пунктирной линией) и перемещаем ее в
направлении вектора-градиента до
последней точки соприкосновения с ОДР
для определения оптимального решения
на![]() ,
это есть точка А. Она лежит на пересечении
прямых
,
это есть точка А. Она лежит на пересечении
прямых![]() и
и![]() .
Для определения ее координат необходимо
решить систему уравнений:
.
Для определения ее координат необходимо
решить систему уравнений:
Откуда
![]() .
Таким образом,
.
Таким образом,![]() .
Подставив значение
.
Подставив значение![]() и
и![]() в целевую функциюZ,
получаем:
в целевую функциюZ,
получаем:
![]() .
.
Затем
перемещаем линию уровня в направлении,
противоположном вектору-градиенту до
последней точки соприкосновения с ОДР
для определения оптимального решения
на
![]() .
Оптимальным решением на
.
Оптимальным решением на![]() является точка В, которая лежит на
пересечении прямых
является точка В, которая лежит на
пересечении прямых![]() и
и![]() .
Для определения ее координат необходимо
решить систему уравнений:
.
Для определения ее координат необходимо
решить систему уравнений:
Откуда
![]() .
Таким образом,
.
Таким образом,![]() .
Подставив значение
.
Подставив значение![]() и
и![]() в целевую функциюZ,
получаем:
в целевую функциюZ,
получаем:
![]() .
.
Ответ:
![]() ,
,![]() ;
;![]() ,
,![]() .
.
Пример 1.9
Графическим методом решить ЗЛП:
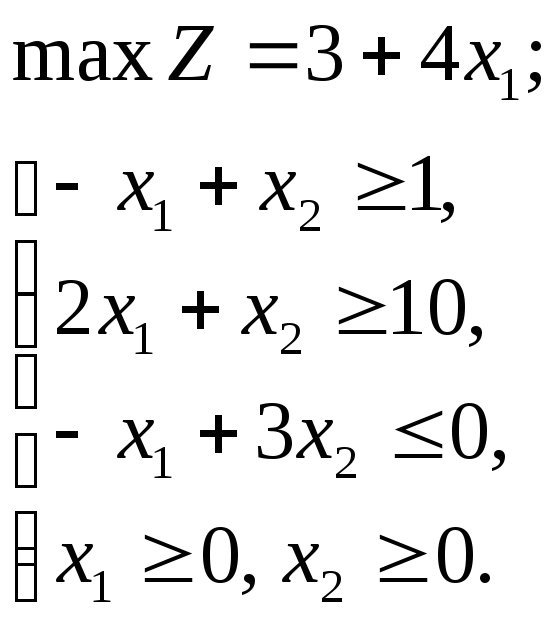
Решение
Вначале
построим ОДР задачи (рис. 1.5). Для этого
в системе координат
![]() на плоскости изобразим граничные прямые:
на плоскости изобразим граничные прямые:
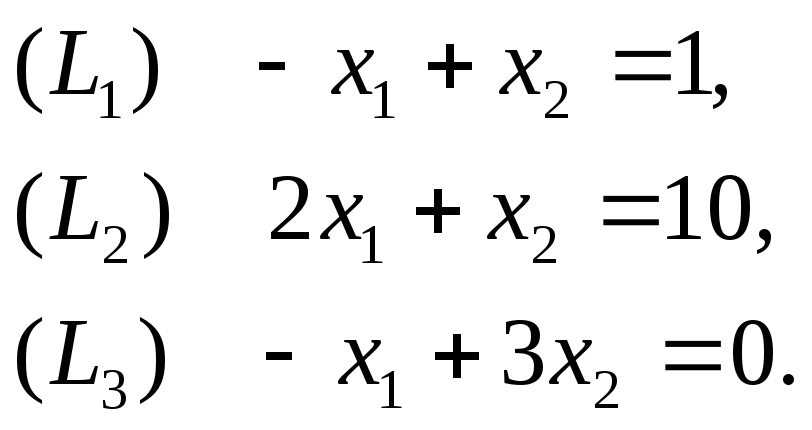
Затем
определим, какую полуплоскость определяет
соответствующее неравенство, подставив
координаты какой-нибудь точки, не лежащей
на этой прямой. Ограничения
![]() означают, что ОДР лежит вI
четверти системы координат
означают, что ОДР лежит вI
четверти системы координат
![]() .
Соответствующие полуплоскости на
рисунке показаны стрелками. Указанные
полуплоскости не имеют ни одной общей
точки, следовательно, ОДР – пустое
множество и задача не имеет решения
вследствие несовместности системы
ограничений.
.
Соответствующие полуплоскости на
рисунке показаны стрелками. Указанные
полуплоскости не имеют ни одной общей
точки, следовательно, ОДР – пустое
множество и задача не имеет решения
вследствие несовместности системы
ограничений.

Рис. 1.5
Пример 1.10
Графическим методом решить ЗЛП:
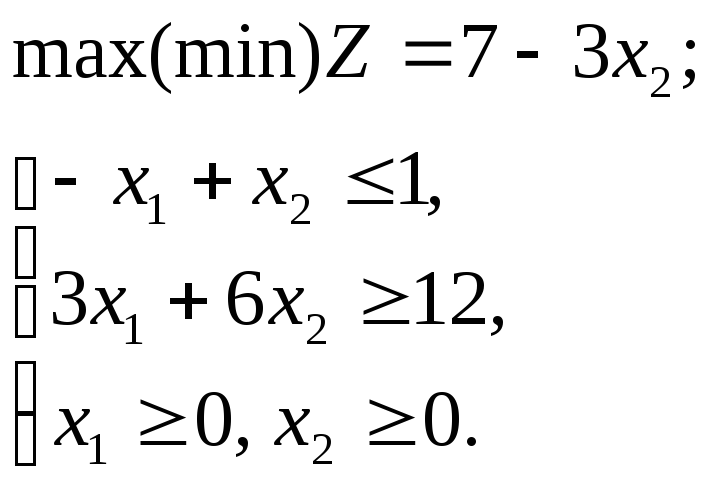
Решение
Вначале
построим ОДР задачи (рис. 1.6). Для этого
в системе координат
![]() на плоскости изобразим граничные прямые:
на плоскости изобразим граничные прямые:
![]()
Затем
определим, какую полуплоскость определяет
соответствующее неравенство, подставив
координаты какой-нибудь точки, не лежащей
на этой прямой. Ограничения
![]() означают, что ОДР лежит вI
четверти системы координат
означают, что ОДР лежит вI
четверти системы координат
![]() .
Соответствующие полуплоскости на
рисунке показаны стрелками. Пересечение
указанных полуплоскостей и определяет
ОДР данной задачи – это открытая
многоугольная областьABCD.
.
Соответствующие полуплоскости на
рисунке показаны стрелками. Пересечение
указанных полуплоскостей и определяет
ОДР данной задачи – это открытая
многоугольная областьABCD.
Строим
вектор-градиент целевой функции
![]() =(0;–3).
Берем произвольную линию уровня целевой
функции (на рисунке она обозначена
пунктирной линией) и перемещаем ее в
направлении вектора-градиента до
последней точки соприкосновения с ОДР
для определения оптимального решения
на
=(0;–3).
Берем произвольную линию уровня целевой
функции (на рисунке она обозначена
пунктирной линией) и перемещаем ее в
направлении вектора-градиента до
последней точки соприкосновения с ОДР
для определения оптимального решения
на![]() .
Такой точкой является любая точка лучаCD.
Следовательно, на
.
Такой точкой является любая точка лучаCD.
Следовательно, на
![]() задача имеет бесконечное множество
решений – это лучCD.
Для нахождения значения целевой функции
на этих решениях, найдем координаты
любой точки этого луча. Так, например,
возьмем С(4;0) и
задача имеет бесконечное множество
решений – это лучCD.
Для нахождения значения целевой функции
на этих решениях, найдем координаты
любой точки этого луча. Так, например,
возьмем С(4;0) и
![]() .
.
Затем
перемещаем линию уровня в направлении,
противоположном вектору-градиенту, при
этом линия уровня уходит в бесконечность,
следовательно, на
![]() задача не имеет решения вследствие
неограниченности целевой функции.
задача не имеет решения вследствие
неограниченности целевой функции.

Рис. 1.6
Ответ:
Оптимальные решения на
![]() – лучCD,
– лучCD,
![]() .
.
Задачи
Решить ЗЛП графическим методом (1.3.1 – 1.3.12)
|
1.3.1 а)
в)
д)
ж)
и)
л)
н)
1.3.2 а)
в)
д)
ж)
1.3.3 а)
в)
д)
1.3.4
1.3.6
1.3.8
1.3.10
1.3.12
|
б)
г)
е)
з)
к)
м)
о)
б)
г)
е)
з)
б)
г)
е)
1.3.5
1.3.7
1.3.9
1.3.11
1.3.13
|
1.3.14 – 1.3.16
Решить задачи 1.1.1 – 1.1.3 (соответственно) графическим методом.