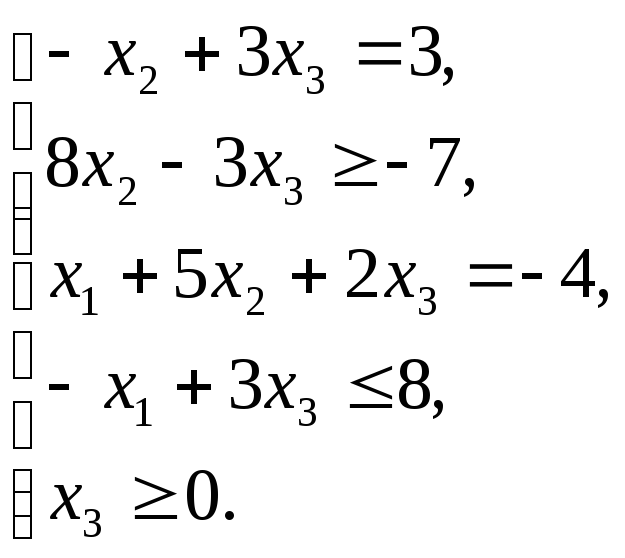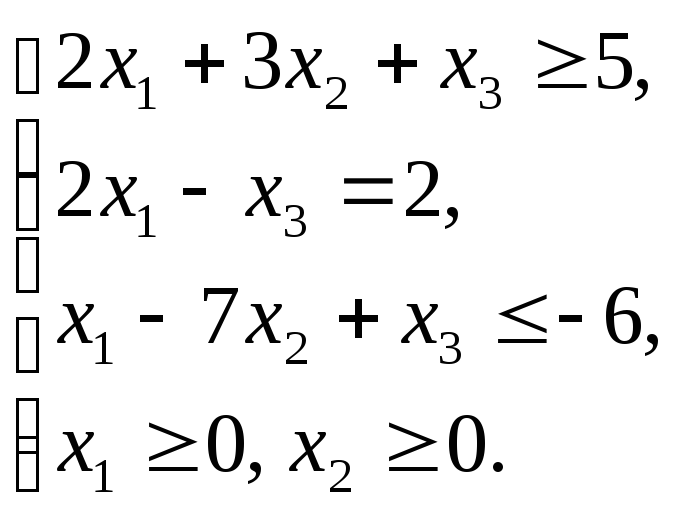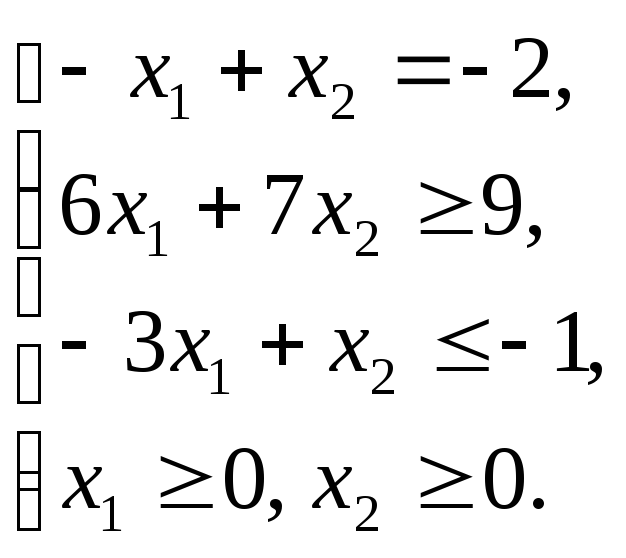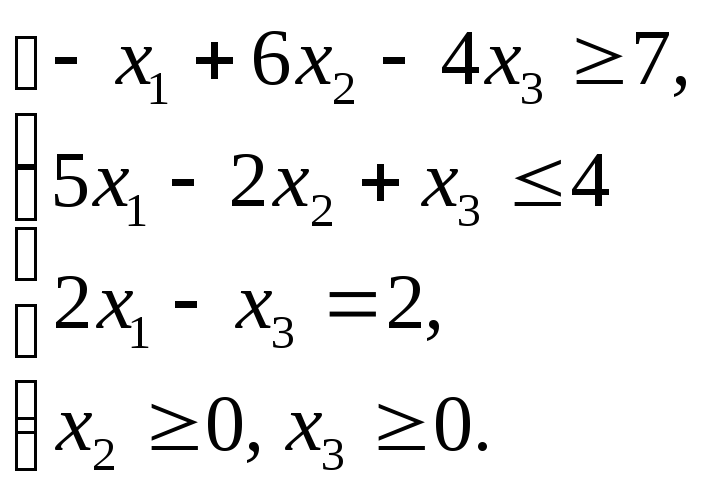- •Глава 1. Линейное программирование 3
- •Глава 2. Транспортная задача линейного программирования (тз) 68
- •Глава 3. Динамическое программирование 98
- •Глава 1. Линейное программирование
- •1.1. Математическая модель задачи линейного программирования
- •1.2. Формы записи задач линейного программирования
- •Рассмотрим приемы, позволяющие переходить от одной формы записи задачи к другой
- •1.3. Геометрическая интерпретация и графический метод решения задач линейного программирования с двумя переменными
- •Алгоритм графического метода решения злп с двумя переменными
- •1.4. Графический метод решения задач линейного программирования сnпеременными
- •1.5. Симплексный метод решения задач линейного программирования
- •Алгоритм решения злп симплексным методом
- •Нахождение начального опорного плана злп ( )
- •Нахождение начального опорного плана злп методом искусственного базиса
- •Нахождение начального опорного плана злп методом Жордановых исключений
- •Шаг Жордановых исключений осуществляется по следующим правилам:
- •Исследование на оптимальность опорного плана при решении злп на
- •Переход к новому опорному плану
- •1.6. Двойственные задачи линейного программирования
- •Правила построения двойственной задачи.
- •Глава 2. Транспортная задача линейного программирования (тз)
- •2.1. Математическая модель транспортной задачи
- •Закрытая и открытая модели транспортной задачи
- •2.2. Решение транспортной задачи
- •Алгоритм решения транспортной задачи
- •Нахождение начального опорного плана методом «минимального элемента»
- •Нахождение начального опорного плана методом «северо-западного угла»
- •Нахождение начального опорного плана методом Фогеля
- •Проверка на оптимальность невырожденного опорного плана методом потенциалов
- •Переход к новому опорному плану
- •Цикл пересчета
- •Глава 3. Динамическое программирование
- •3.1. Задача оптимального распределения ресурсов
- •I этап. Условная оптимизация.
- •II этап. Безусловная оптимизация.
- •3.2. Задача об оптимальной стратегии замены оборудования
- •I этап. Условная оптимизация.
- •II этап. Безусловная оптимизация.
- •Список использованной литературы
1.2. Формы записи задач линейного программирования
Общая задача линейного программирования (ОЗЛП) – это ЗЛП, у которой все переменные неотрицательны, т.е. ее математическая модель имеет вид:
![]()
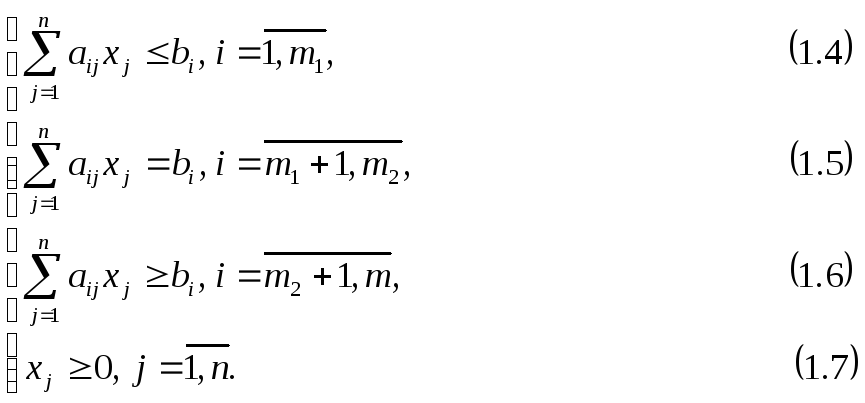
где ![]() – заданные действительные числа.
– заданные действительные числа.
Симметричной (стандартной) формой записи ЗЛП называется задача максимизации целевой функции (1.3) при ограничениях вида (1.4) и (1.7) или задача минимизации целевой функции (1.3) при ограничениях вида (1.6) и (1.7), т. е.
 или
или
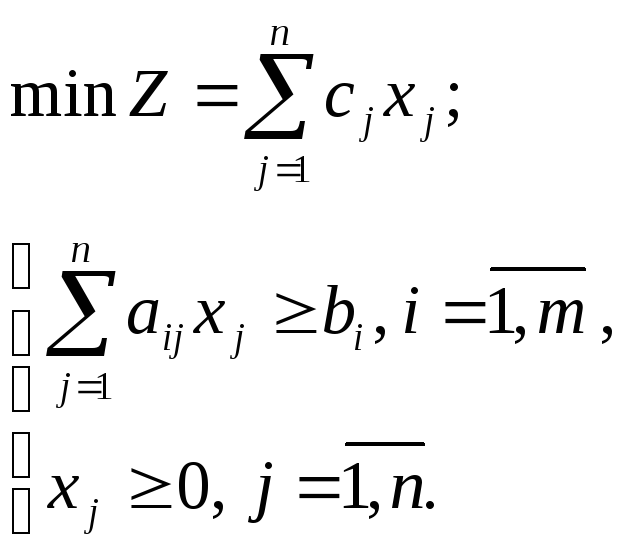
где ![]() – заданные действительные числа.
– заданные действительные числа.
Канонической формой записи ЗЛП называется задача минимизации или максимизации целевой функции (1.3) при ограничениях вида (1.5) и (1.7), т. е.
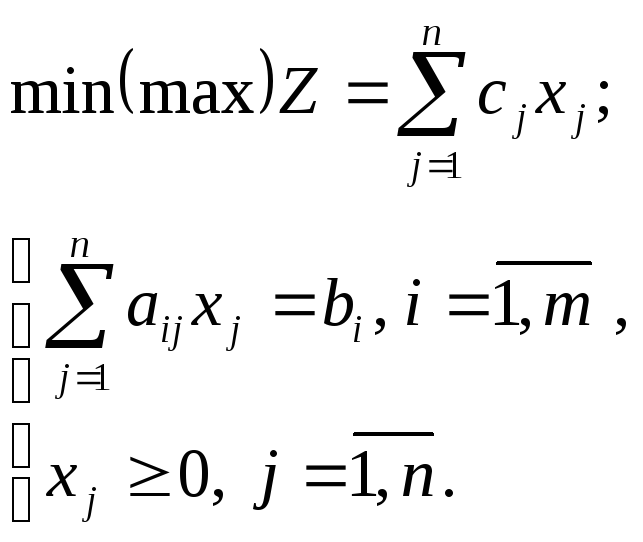
Рассмотрим приемы, позволяющие переходить от одной формы записи задачи к другой
Переход от задачи на минимум целевой функции к задаче на максимум целевой функции осуществляется умножением ее на (–1). Действительно, если функция
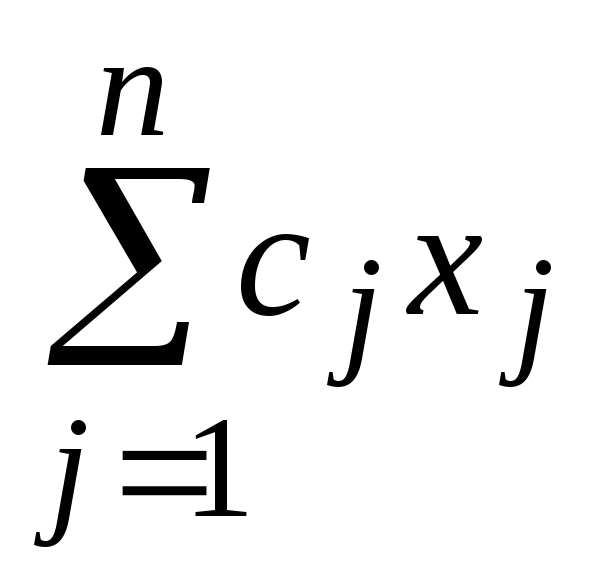 достигает минимума при значениях
достигает минимума при значениях
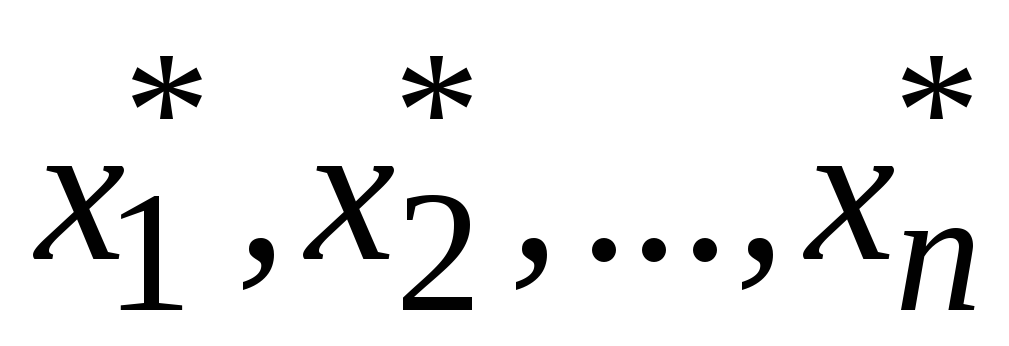 ,
то функция (
,
то функция (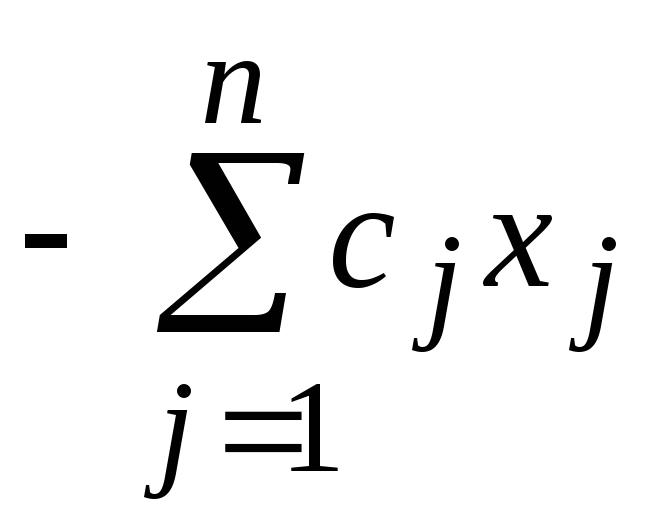 )достигает
при тех же значениях переменных
максимума.
)достигает
при тех же значениях переменных
максимума.Переход от неравенства вида « » к неравенству вида « » (и наоборот) также осуществляется умножением исходного неравенства на (–1).
Переход от неравенства к равенству осуществляется введением дополнительной неотрицательной переменной. Так если в исходной модели
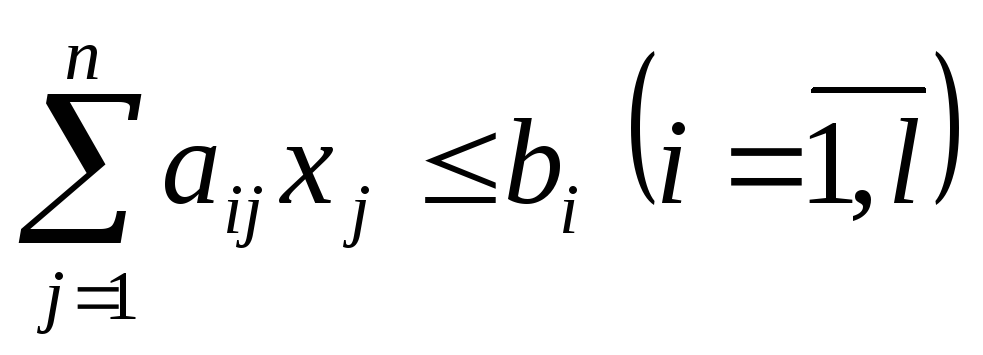 ,
то, вводя
,
то, вводя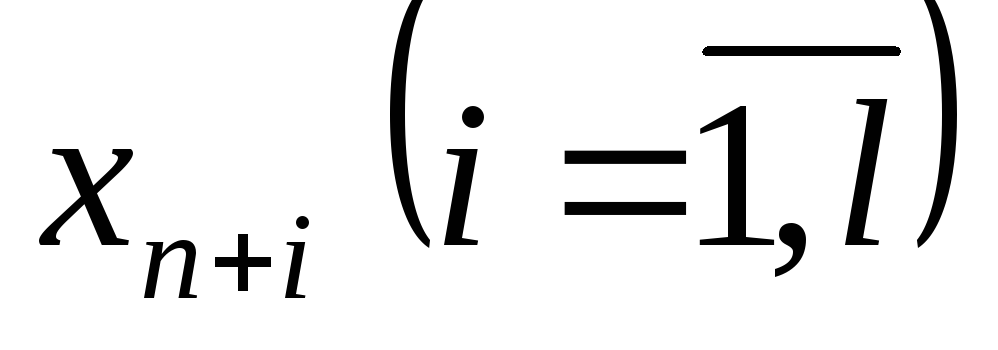 ,
получим
,
получим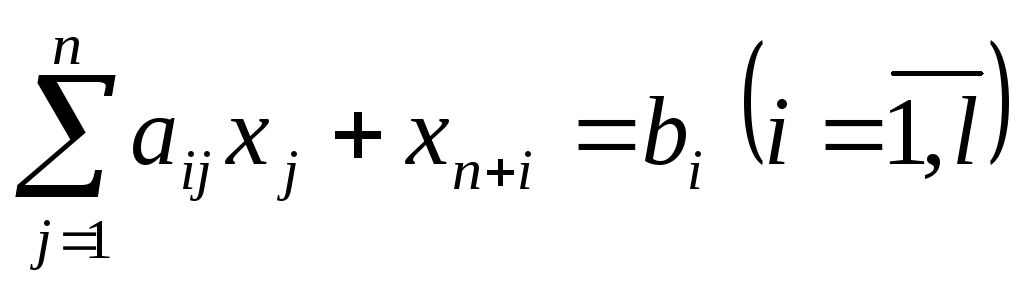 ,
а если в исходной модели
,
а если в исходной модели ,
то, вводя
,
то, вводя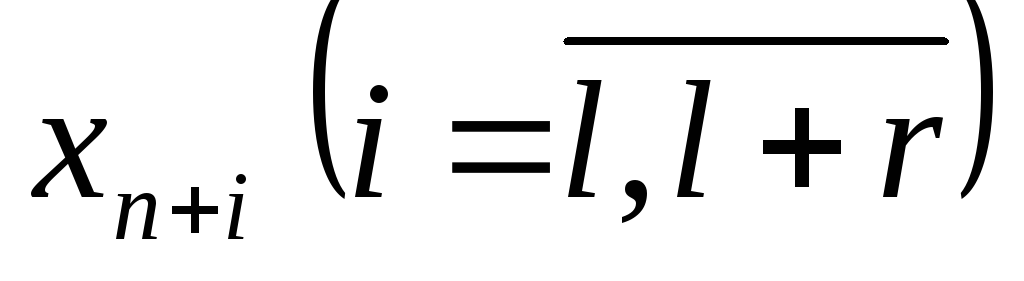 ,
получим
,
получим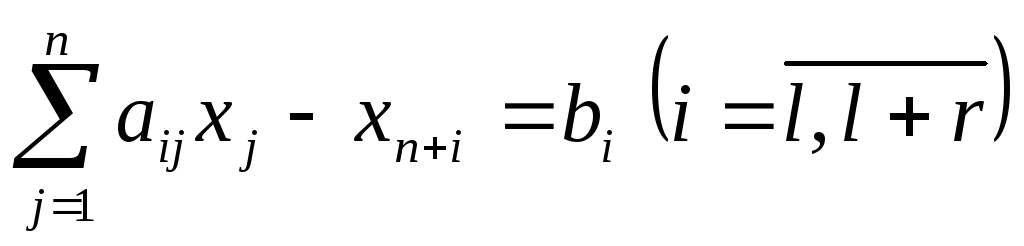 ,
где
,
где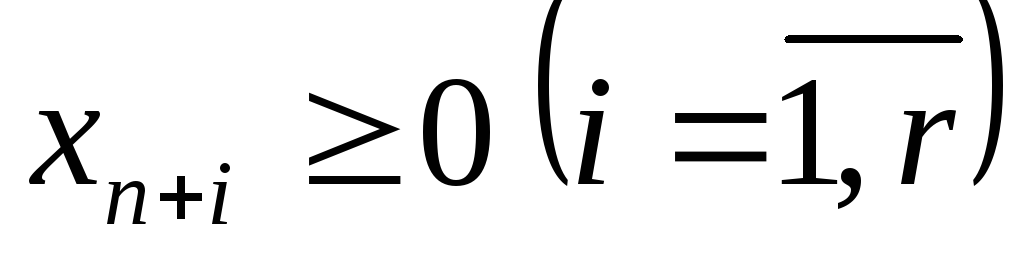 .
.При переходе от равенств к неравенствам можно руководствоваться следующим: любое уравнение
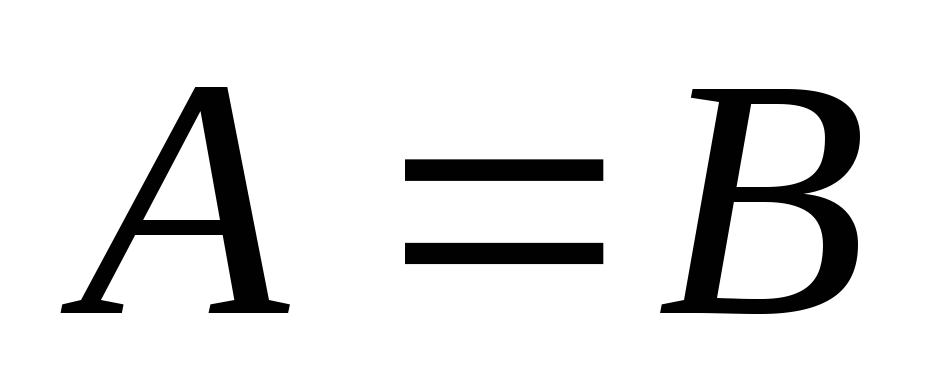 эквивалентно системе двух неравенств:
эквивалентно системе двух неравенств: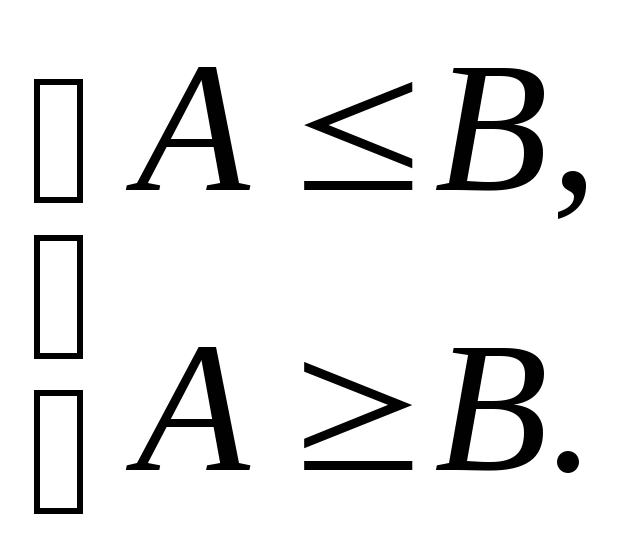
Введение условия неотрицательности переменной. Пусть на переменную
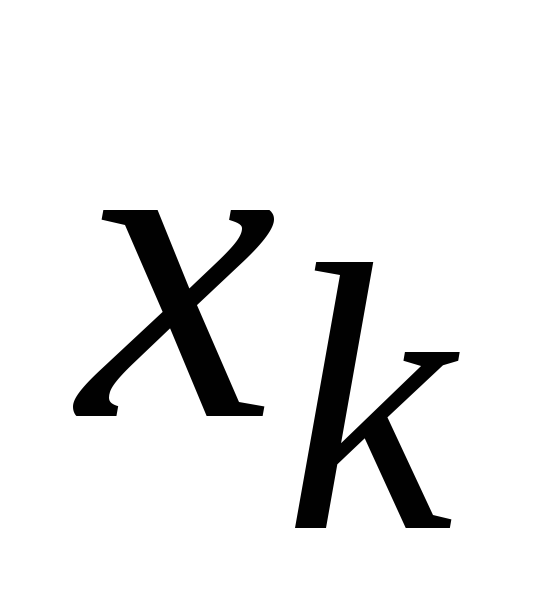 это условие не было наложено (т.е.
это условие не было наложено (т.е.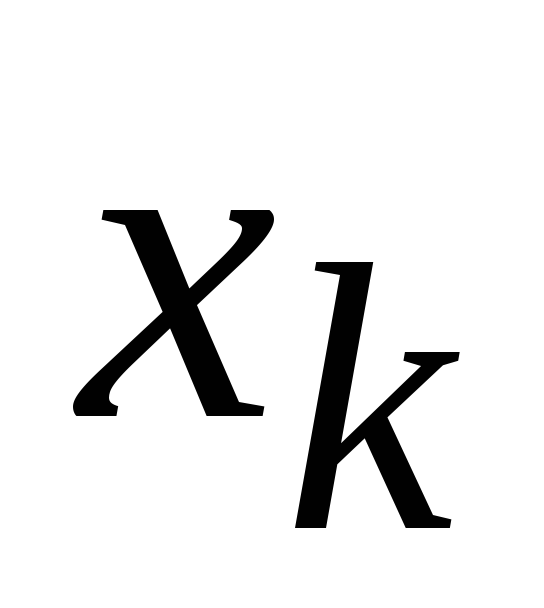 может быть любого знака). Тогда вместо
этой переменной можно ввести две
неотрицательные переменные
может быть любого знака). Тогда вместо
этой переменной можно ввести две
неотрицательные переменные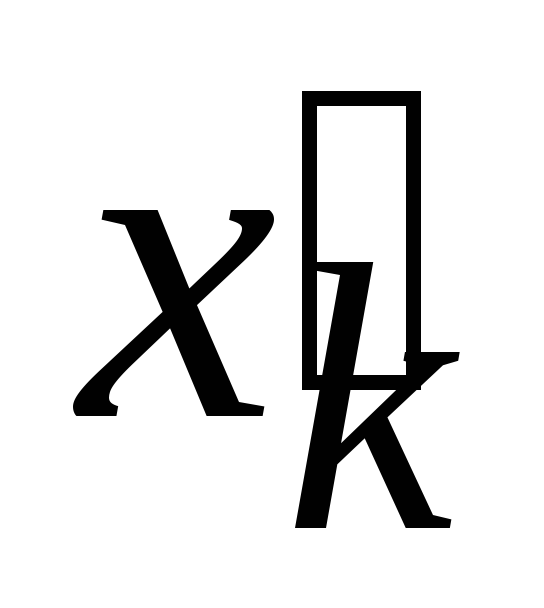 и
и ,
и представить
,
и представить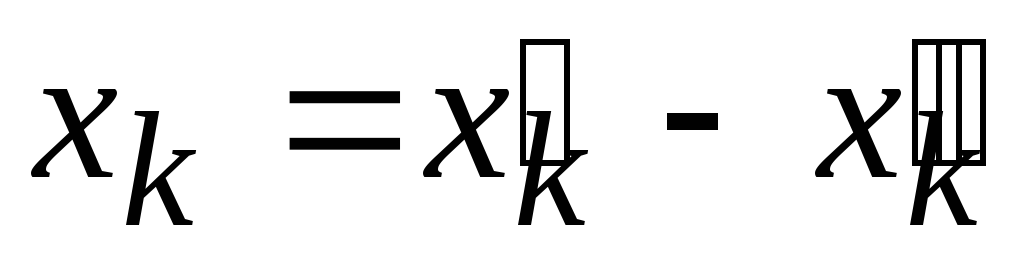 ,
где
,
где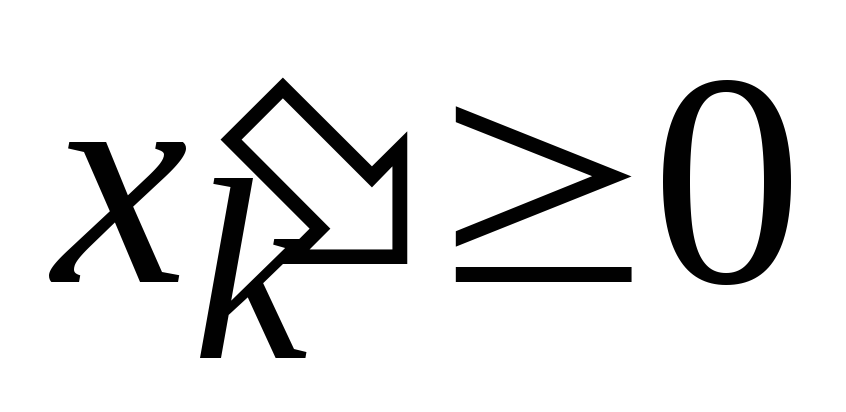
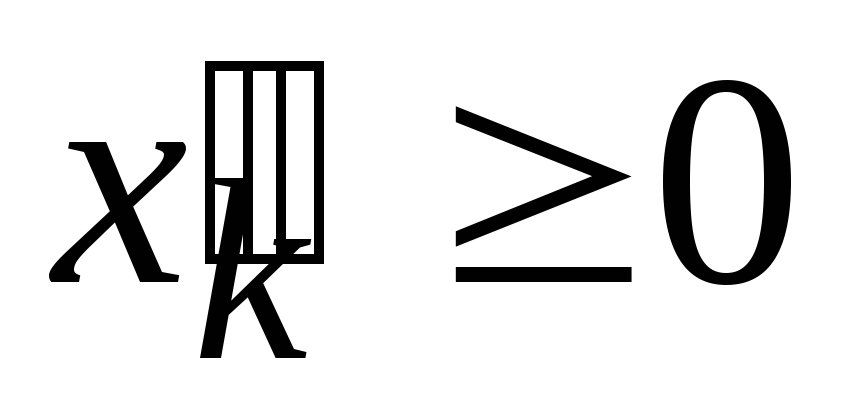 .
Это всегда возможно.
.
Это всегда возможно.
Изложенными приемами любая ЗЛП может быть сведена к ОЗЛП, симметричной и канонической формам записи ЗЛП, которые используются для решения ЗЛП. Однако, поскольку в процессе таких преобразований мы вводили дополнительные переменные, то после того, как задача решена, нужно произвести обратный переход к исходным переменным, определяющим непосредственный экономический смысл задачи.
Пример 1.4
Пусть математическая модель задачи имеет следующий вид:
![]() ;
;
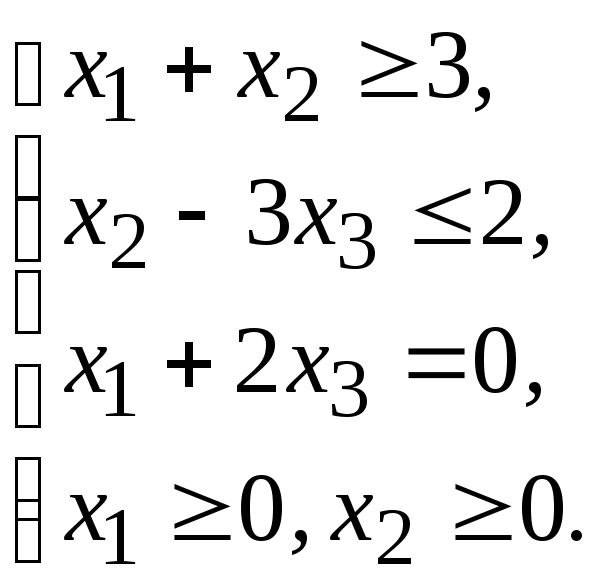
Записать для данной модели
а) ОЗЛП,
б) симметричную форму,
в) каноническую форму.
Решение
а)
Чтобы получить общую задачу линейного
программирования, необходимо, чтобы на
все переменные было наложено условие
неотрицательности. Для наложения этого
ограничения на переменную
![]() воспользуемся правилом 5. Введем две
новые неотрицательные переменные
воспользуемся правилом 5. Введем две
новые неотрицательные переменные![]() и
и![]() и представим
и представим![]() ,
где
,
где![]() и
и![]() .
.
Тогда ОЗЛП будет иметь вид:
![]() ;
;
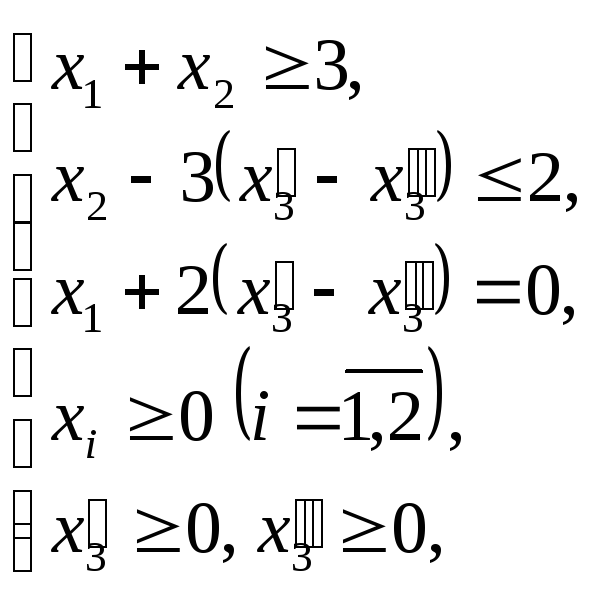
или (раскрыв скобки):
![]() ;
;

Обратите внимание, что в ОЗЛП число переменных на одну увеличилось.
б) Для составления симметричной формы воспользуемся полученной ОЗЛП (т.к. в симметричной форме также на все переменные должно быть наложено условие неотрицательности). Чтобы получить все ограничения вида « » (т.к. целевая функция на минимум) необходимо ограничение (1.9) умножить на (–1) (правило 2), а ограничение-равенство (1.10) заменить предварительно двумя ограничениями-неравенствами (правило 4):
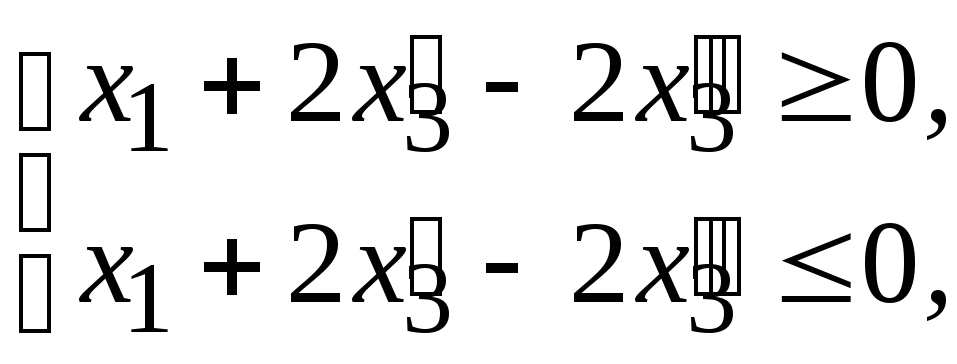
откуда, умножив второе ограничение системы на (–1), получим ограничение (1.11) вида « ». Таким образом, симметричная форма будет иметь вид:
![]() ;
;
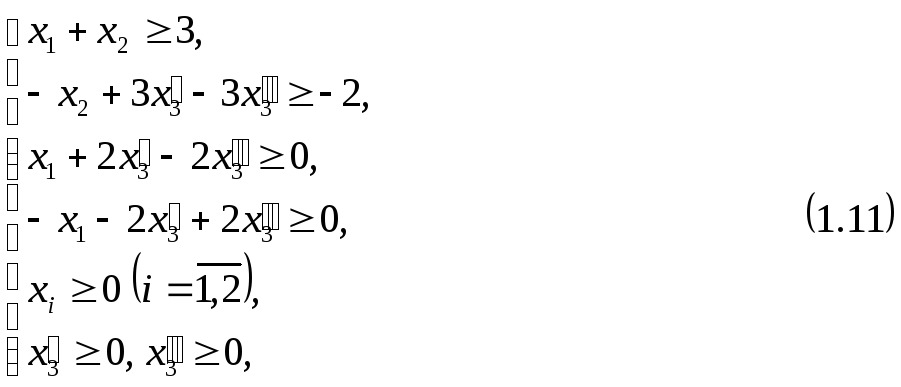
где
![]() .
.
Обратите внимание, что в симметричной форме увеличилось число ограничений (за счет замены одного ограничения-равенства двумя ограничениями-неравенствами) и число переменных (за счет замены одной переменной любого знака на разность двух неотрицательных переменных).
в)
Для составления канонической формы
воспользуемся полученной ОЗЛП (т.к. в
канонической форме также на все переменные
должно быть наложено условие
неотрицательности). Чтобы получить все
ограничения вида « = » необходимо из
ограничений-неравенств (1.8 – 1.9) получить
эквивалентные ограничения-равенства.
Согласно правилу 3 для этого от левой
части ограничения (1.8) отнимем новую
неотрицательную переменную
![]() ,
а к левой части ограничения (1.9) прибавим
новую неотрицательную переменную
,
а к левой части ограничения (1.9) прибавим
новую неотрицательную переменную![]() .
Таким образом, каноническая форма будет
иметь вид:
.
Таким образом, каноническая форма будет
иметь вид:
![]() ;
;

где
![]() .
.
Пример 1.5
Пусть математическая модель задачи имеет следующий вид:
![]() ;
;
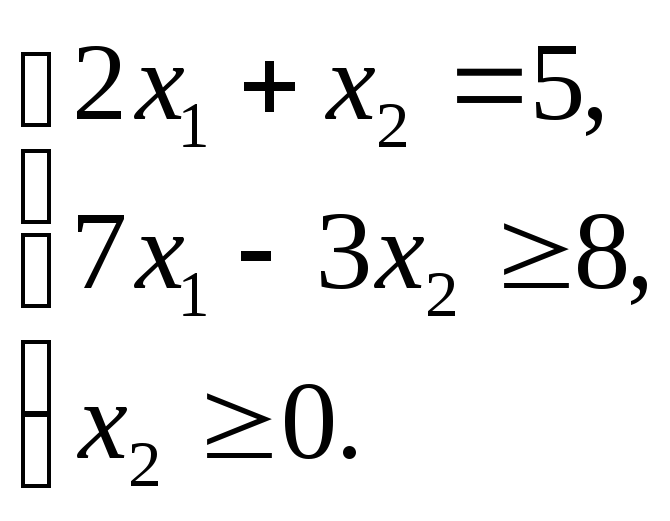
Записать для данной модели
а) ОЗЛП,
б) симметричную форму,
в) каноническую форму.
Решение
а)
Чтобы все переменные задачи были
неотрицательны, представим
![]() ,
где
,
где![]() и
и![]() .
.
Тогда ОЗЛП будет иметь вид:
![]() ;
;
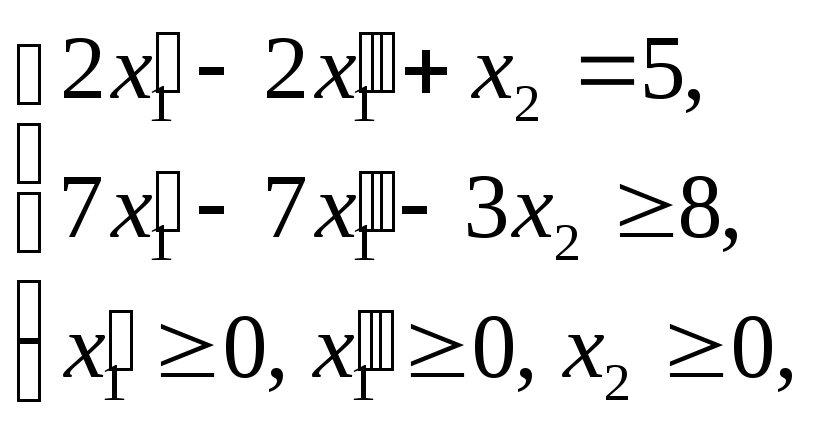
где
![]() .
.
б) Для составления симметричной формы воспользуемся полученной ОЗЛП. Симметричная форма будет иметь вид:
![]() ;
;
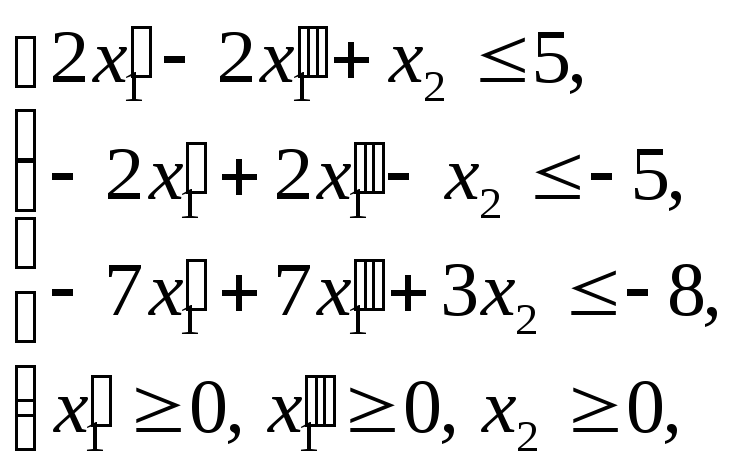
где
![]() .
.
в) Для составления канонической формы воспользуемся полученной ОЗЛП. Каноническая форма будет иметь вид:
![]() ;
;
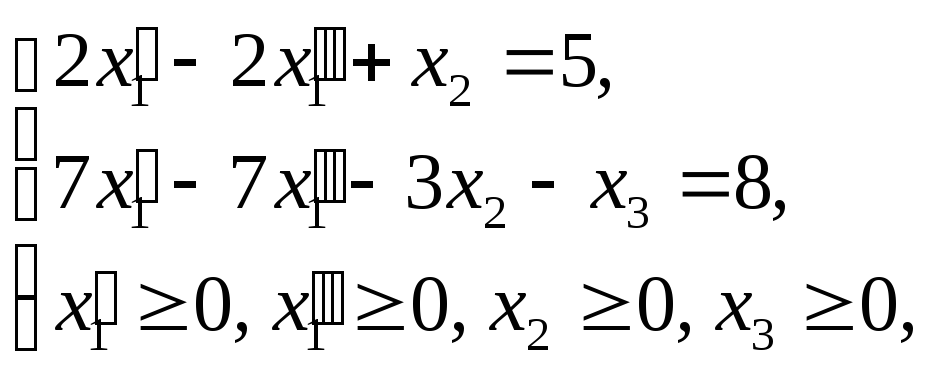
где
![]() .
.
Задачи
Записать для данной модели (1.2.1 – 1.2.6)
а) ОЗЛП,
б) симметричную форму,
в) каноническую форму.
|
1.2.1
1.2.3
1.2.5
|
1.2.2
1.2.4
1.2.6
|