
Теория_Вероятностей_КР7
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования
РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ
КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
(теория, практика, контрольная работа №7)
Ростов-на-Дону
2009
УДК 517(07)
Теория вероятностей (теория, практика, контрольная работа №7). — Ростов-на-Дону: Ростовский государственный строительный университет, 2009 – 76 с.
Пособие предназначено для студентов заочной формы обучения. Содержит основные понятия теории вероятностей, формулировки теорем, соответствующие формулы, примеры с подробными решениями. Приведены контрольные задания.
Кафедра прикладной математики и вычислительной техники РГСУ Составители: д.т.н. Белявский Г.И. к.ф.-м.н. Мисюра В.В.
♥РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ, 2009

1
1. Некоторые формулы комбинаторики
При решении вероятностных задач часто приходится в заданном множестве выбирать подмножества элементов, которые обладают определенными свойствами. Поскольку в таких задачах речь идет про те или иные комбинации объектов, то их называют комбинаторными задачами.
Пусть некоторое множество А содержит n элементов.
Будем выбирать из множества А m элементов. Тогда каждая выборка из m элементов может быть записана в виде {a1,a2,...,am}, где ai — номер элемента,
извлеченного на i-м шаге.
Будем различать два случая: упорядоченные выборки и неупорядоченные выборки. В первом случае выборки, состоящие из одних и тех же элементов, но отличающиеся порядком следования этих элементов, объявляются различными. Во втором случае порядок следования элементов не принимается во внимание, и такие выборки являются тождественными. Далее упорядоченные выборки бу-
дем обозначать (a1, a2 ,..., am ), а неупорядоченные [a1,a2 ,...,am ].
Рассмотрим различные способы выбора m элементов из n различных элементов. Возможны два варианта последовательного выбора элементов: без возвращения ai в исходное множество перед извлечением ai+1 и с возвращением ai в
исходное множество перед извлечением ai+1.
1.Выбор без возвращения.
Будем предполагать, что m ≤ n и, что извлеченные из множества A элементы обратно не возвращаются. В этом случае рассматривается две возможности, связанные с различением упорядоченных и неупорядоченных выборок.
Будем выбирать из множества А различные упорядоченные подмножества из m элементов. Размещениями из n элементов по m назовем все упорядоченные наборы (ai1 ,ai2 ,...,aim ) элементов множества А.
Через Anm обозначают число всех размещений из n элементов по m элементов (читается: «А из n по m») и
Anm = n (n −1) ... (n − (m −1)). |
(1.1) |
Для упрощения расчетов воспользуемся понятием факториала.
Напомним, что символ k! (читается: «k (ка) факториал») есть сокращенное обозначение произведения 1 2 3 ... k .
Например: 5!= 1 2 3 4 5 = 120 . Заметим, что 0!= 1.
Тогда
2
|
Am = |
|
|
n! |
|
|
, где 0 ≤ m ≤ n . |
|
|
|
|
(1.2) |
||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
n |
(n − m)! |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||
Например: |
An1 = |
n! |
|
|
= 1 2 3 ... (n −1) n |
= n, An0 |
= |
n! |
|
= 1. |
||||
(n −1)! |
(n − 0)! |
|||||||||||||
|
|
|
1 2 3 ... (n −1) |
|
|
|
||||||||
Пример 1.1. Пусть даны четыре цифры: 1; 2; 3; 4. Определим сколько двузначных чисел можно составить из этих цифр, так чтобы цифры в полученном числе не совпадали.
Решение. Очевидно, что полученные двузначные цифра можно представить как
размещения из 4 элементов по 2. Имеем A2 |
= |
|
4! |
|
= 4 3 = 12 . Следовательно, |
|
|
|
|||
4 |
|
(4 |
− 2)! |
|
|
|
|
|
|||
можно составить 12 двузначных чисел, запись каждого из которых состоит из не-
совпадающих цифр: 12, 13, 14, 21, 23, 24, 31, 32, 34, 41, 42, 43. ►
Частный случай размещения при m=n называется перестановкой из n эле-
ментов. Т.е. комбинации из n элементов отличаются только порядком расположения этих элементов. Число всех перестановок из n элементов обозначается Pn
и вычисляется по формуле
Рn = Ann = n!. |
(1.3) |
Пример 1.2. На книжной полке выставлены 8 книг различных авторов. Сколько способов имеется для расстановки этих книг в разном порядке?
Решение. Имеем Р8 = 8!= 1 2 3 4 5 6 7 8 = 40320 . Т.о. имеется 40 320 способов переставить 8 книг в разном порядке.►
Пусть теперь из множества А выбирается без возвращения неупорядоченное подмножество, состоящее из m элементов. Сочетаниями из n элементов по m на-
зываются подмножества из m элементов, отличающиеся друг от друга хотя бы одним элементом. Общее число всех сочетаний из n по m обозначается Cnm (читается: «С из n по m»). Из неупорядоченного набора [a1 ,a2 ,...,am ], состоящего из различных элементов, можно получить m! упорядоченных наборов. Следовательно, Cnm m! = Anm и число сочетаний вычисляется по формуле:
|
m |
|
n! |
|
|
(1.4) |
Cnm = |
An |
= |
= n(n −1)...(n − m + 1) . |
|
||
m! |
(n − m)!m! |
|
||||
|
|
m! |
|
|||
Заметим, что справедливо равенство Cnm = Cnn−m .
Пример 1.3. В шахматном турнире участвуют 8 человек. Сколько партий должно быть сыграно в турнире, если между любыми двумя участниками должна быть сыграна одна партия?
3
Решение. Каждая партия играется двумя участниками из 8 и отличается от других только составом пар участников, т.е. представляет собой сочетание из 8 эле-
ментов по 2. Т.о. имеем C 2 |
= |
|
8! |
|
= |
8! |
|
= 8 7 = 28. ► |
|
|
|
|
|||||
8 |
|
(8 |
− 2)!2! |
6!2! |
2 1 |
|||
|
|
|||||||
2. Выбор с возвращением.
В случае упорядоченных выборок любое множество, состоящее из элементов множества A имеет следующую структуру (ai1 ,ai2 ,...,aim ), где каждое aik +1 из-
влекается после возвращения aik во множество А. Число различимых множеств
(ai1 ,ai2 ,...,aim ), называемых в комбинаторике размещениями из n элементов по m с
возвращением (обозначение A(mn) ), равно nm , т.е.
A(mn) = nm (читается: «А из n по m с повторениями»). |
(1.5) |
Если же рассматриваются неупорядоченные выборки с возвращением, то
множества [ai1 ,ai2 ,...,aim ], составленные из элементов множества A называются сочетаниями из n элементов по m c повторениями. Число таких подмножеств обозначается C(mn) и вычисляется по формуле
C(mn) = Cnm+m−1. |
(1.6) |
Пример 1.4. Сколько различных пятизначных чисел можно составить, используя цифры а) 1, 2, 3, 4; б) 0, 1, 2.
Решение. а) Пусть множество A = {1,2,3,4}. Любое пятизначное число b1b2b3b4b5 , составленное из цифр 1, 2, 3, 4, можно представить как множество (b1,b2 ,b3 ,b4 ,b5 ), где bi — любой элемент из множества A. Например, число 11244, можно представить как упорядоченное множество (1,1,2,4,4). Очевидно, что упорядоченные множества, состоящие из пяти элементов, выбранных из четырех заданных по схеме выбора с возвращением, являются размещениями из 4 элементов по 5 с возвращением и A(54) = 45 = 1024 .
б) Пусть множество A = {0,1,2}. Если не учитывать, что первой цифрой 0 быть не может, то число всех упорядоченных множеств выбранных из множества А по схеме с возвращением равно A(53) . Для подсчета числа всех пятизначных чисел
(обозначим N), составленных из цифр 0, 1, 2, необходимо из A(53) вычесть число упорядоченных множеств, первым элементом которых является 0. Тогда N = A(53) − A(43) = 35 − 34 = 2 34 = 162 . Этот же результат можно получить, рассуждая следующим образом. Первую цифру слева можно выбрать двумя способами,
4
каждую из оставшихся четырех цифр можно выбрать тремя способами. Тогда
N = 2 3 3 3 3 = 162 .►
Пример 1.5. Сколькими способами можно составить портфель из 20 акций, если возможно купить акции лишь 4 компаний?
Решение. Пусть A = {a1, a2 , a3 , a4 }, где ai — акция i-й компании (i=1,2,3,4). Вы-
борки имеют объем равный 20. Поскольку порядок расположения акций в выборке не играет роли, т.е. выборка является неупорядоченным множеством, то искомое число портфелей будет равно числу сочетаний с повторениями из 4 элементов
по 20. Имеем C(4)20 = C420+20−1 = C2320 = |
23! |
|
= |
21 22 23 |
= 1771.► |
|
20!3! |
1 2 3 |
|||||
|
|
|
||||
Результаты о числе множеств, полученных в результате извлечения m элементов из множества A, состоящего из n различных элементов сведем в таблицу 1.
nm |
C(mn) = Cnm+ m−1 |
Am |
C m |
n |
n |
Упорядоченный Неупорядоченный
Таблица1
Без возвра- С возвращещения нием
Выбор
Набор
Для случая n = 3 и m = 2 ( A = {1,2,3}) выборки по соответствующим схемам приводятся в таблице 2.
Таблица2
(1, 1) (1, 2) (1, 3) |
[1, 1] [2, 2] [3,3] |
|
(2, 1) (2, 2) (2, 3) |
[1, 2] [1, 3] |
|
(3, 1) (3, 2) (3, 3) |
[2, 3] |
|
|
|
|
(1, 2) (1, 3) |
[1, 2] [1, 3] |
|
(2, 1) (2, 3) |
||
[2, 3] |
||
(3, 1) (3, 2) |
||
|
||
|
|
|
Упорядоченный |
Неупорядоченный |
|
|
|
С возвра- |
щением |
Без воз- |
вращения |
Выбор
Набор
5
2.События и вероятность
2.1.Случайные события.
Опытом, испытанием, случайным экспериментом будем называть выполнение определенного комплекса условий, в результате чего осуществляется регистрация наблюдения.
Непосредственные исходы опыта называются элементарными событиями и обозначаются через ω . Элементарные события (их называют также «элементами», «точками», «случаями») рассматриваются как неразложимые и взаимоисключающие исходы опыта.
Множество всех элементарных событий называется пространством элементарных событий Ω (ПЭС) или пространством исходов, т.е. Ω = {ω}.
Рассмотрим несколько примеров описания структуры ПЭС:
Пример 2.1. Опыт — бросание игральной кости: Ω = {ω1 ,ω2 ,ω3 ,ω4 ,ω5 ,ω6 }. Событие ωi означает, что в результате бросания кости выпало i очков, i = 1,2,3,4,5,6. ►
Пример 2.2. Опыт — стрельба по цели до первого попадания:
Ω = {ω1( П ),ω2 (НП),ω3 (ННП),...}, П означает попадание в цель, Н — непопадание.►
Пример 2.3. Опыт — наблюдение за временем безотказной работы некоторого агрегата: Ω = {t,0 ≤ t < ∞}, t — время безотказной работы некоторого агрегата; время t меняется непрерывно. ►
Заметим, что в опыте, приведенном в примере 2.1., Ω конечно, в примере 2.2. – счетно (т. е. элементы этого множества можно пронумеровать с помощью множества натуральных чисел), в примере 2.3. — несчетно (континуально).
!В пределах раздела «События и вероятность» будем рассматривать только конечные ПЭС.
Случайным событием А (или просто событием А) называется любое под-
множество множества Ω : A Ω .
События обозначаются, как правило, заглавными буквами латинского алфа-
вита: A, B,C… .
Элементарные события, входящие в подмножество А пространства Ω , называются благоприятствующими событию А.
Вернемся к первому опыту. Примером события А является выпадение четного числа очков; очевидно, что A = {ω2 ,ω4 ,ω6}. Событию А благоприятствуют
элементарные события ω2 ,ω4 ,ω6 .
6
Допустим подбрасывание игральной кости закончилось выпадением 4-х очков. Согласно определению случайного события событие А наступило или наблюдается.
Т.о. случайное событие может наступить, а может и не наступить. Если опыт заканчивается ω А, то в данном опыте событие А наступило (или произошло), если же ω А, событие А в данном опыте не наступило.
Пусть А= Ω , тогда, каким бы элементарным событием ω не закончился опыт, всегда ω А. Следовательно, такое событие наступает всегда.
Событие называется достоверным, если оно обязательно наступит в результате данного опыта.
Пусть А= , тогда, каким бы элементарным событием ω не закончился опыт, всегда ω А. Следовательно, такое событие не наступит никогда.
Событие называется невозможным, если оно заведомо не наступит в результате проведения опыта.
Так в опыте, подбрасывание игральной кости, событие А — выпадение целого числа очков, является достоверным событием, а событие В — выпадение 7 очков, является невозможным событием.
2.2. Алгебра событий
Введем основные операции над событиями. События и действия над ними можно представить как операции над множествами и наглядно иллюстрировать с помощью диаграмм Эйлера-Венна: достоверное событие Ω изображается прямоугольником; события представляются как подмножества Ω .
Вводимые ниже определения действия над событиями будем иллюстрировать с помощью диаграмм Эйлера-Венна и давать множественную трактовку вводимых определений.
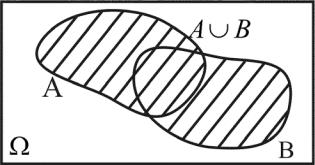
Суммой событий А и В называется событие, состоящее в наступлении хотя бы одного из них.
Сумме двух событий A Ω и B Ω (обозначается А + В или A B ) соответствует объединение множеств А и В (см. рис.1).
Рис.1. А + В
